mcmix
Create random Markov chain with specified mixing structure
Description
mc = mcmix(numStates,Name=Value)
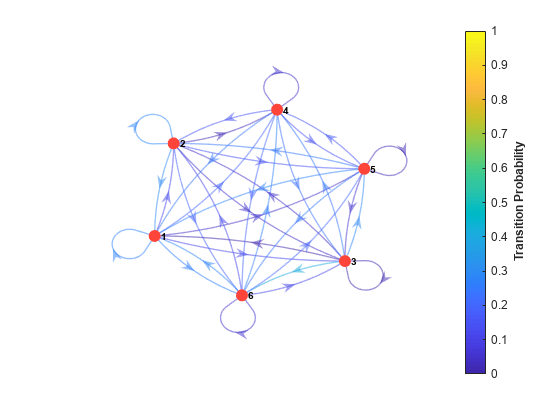
Examples
Input Arguments
Name-Value Arguments
Output Arguments
References
[1] Gallager, R.G. Stochastic Processes: Theory for Applications. Cambridge, UK: Cambridge University Press, 2013.
[2] Horn, R., and C. R. Johnson. Matrix Analysis. Cambridge, UK: Cambridge University Press, 1985.
Version History
Introduced in R2017b