適応ノイズ キャンセリング

与えられた 1 つの信号から 2 番目の信号を予測できるように線形ニューロンの適応が許可されます。

TIME は、このシミュレーションのタイム ステップを定義します。P は、これらのタイム ステップにわたる信号を定義します。T は、P を左にシフトし、2 で乗算してそれ自体に加算することによって導出される信号です。

time = 1:0.01:2.5;
X = sin(sin(time).*time*10);
P = con2seq(X);
T = con2seq(2*[0 X(1:(end-1))] + X);

この 2 つの信号をプロットする方法を以下に示します。

plot(time,cat(2,P{:}),time,cat(2,T{:}),'--')
title('Input and Target Signals')
xlabel('Time')
legend({'Input','Target'})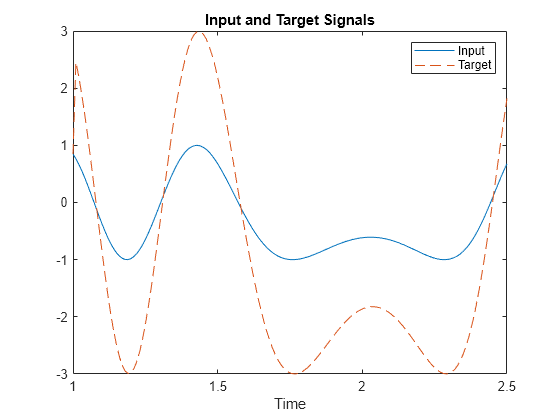

線形ネットワークは、P と T の間の時間シフトした相関を学習するために、タップ遅延をもたなければなりません。linearlayer 関数は線形層を作成します。[0 1] は、遅延のない 1 つの入力と遅延が 1 の 1 つの入力を指定します。最後の引数は学習率です。

net = linearlayer([0 1], 0.1);

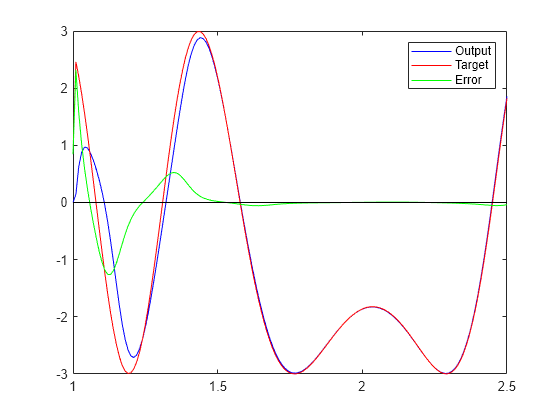
ADAPT は、適応ネットワークをシミュレートします。ネットワーク、信号、およびターゲット信号を取り、信号を適応的にフィルター処理します。出力 Y を青、ターゲット T を赤、誤差 E を緑でプロットします。t=2 までに、ネットワークは入力とターゲットの間の関係を学習し、誤差は 0 の近くまで減少します。

[net,Y,E,Pf]=adapt(net,P,T);
plot(time,cat(2,Y{:}),'b', ...
   time,cat(2,T{:}),'r', ...
   time,cat(2,E{:}),'g',[1 2.5],[0 0],'k')
legend({'Output','Target','Error'})