ノットの選択方法
この例では、Curve Fitting Toolbox™ の optknt コマンドおよび newknt コマンドを使用して、ノットを選択および最適化する方法を示します。
サンプル データ
次に、可変ノットを含むスプライン近似のテストによく使用されるサンプル データ、いわゆるチタン熱データを示します。これは、温度の関数として測定された、チタンの特定のプロパティを記録しています。
[xx,yy] = titanium; plot(xx,yy,'x'); axis([500 1100 .55 2.25]); title('The Titanium Heat Data'); hold on
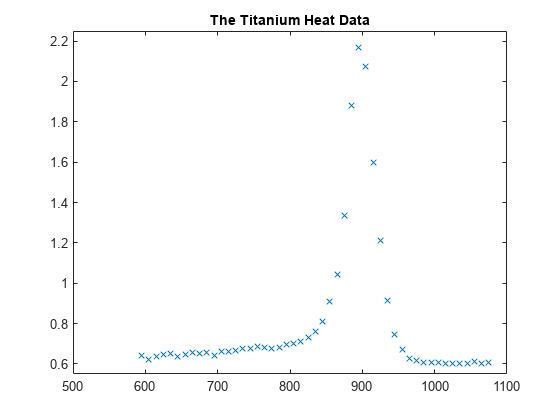
かなりシャープなピークが目に留まります。これらのデータを使用して、ノット選択のメソッドについて説明します。
まず、これらのやや粗いデータからいくつかのデータ点を選択します。このサブセットを使用して内挿した後、その結果をデータセット全体と比較します。
pick = [1 5 11 21 27 29 31 33 35 40 45 49]; tau = xx(pick); y = yy(pick); plot(tau,y,'ro'); legend({'Full Dataset' 'Subsampled Data'}, 'location','NW');
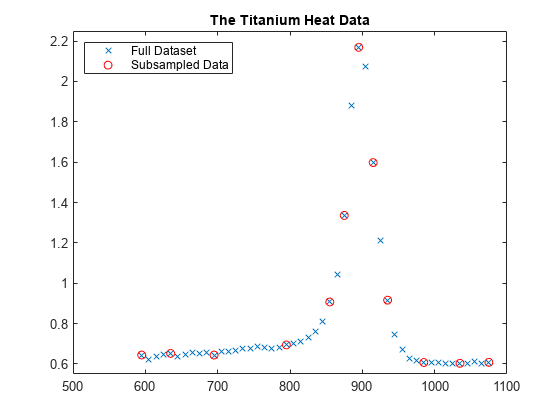
一般的な考慮事項
n+k 個のノットをもつ次数 k のスプラインの自由度は、n となります。データ サイトは tau(1) < ... < tau(12) の 12 個であるため、3 次スプライン、すなわち次数が 4 のスプラインによる近似には、長さ 12+4 のノット シーケンス t が必要です。
また、ノット シーケンス t は "Schoenberg-Whitney 条件" を満たさなければなりません。つまり、i 番目のデータ サイトが i 番目の B スプラインのサポートになるように、言い換えると
t(i) < tau(i) < t(i+k) for all i,
等式は多重度 k のノットの場合にのみ許容されます。
これらの条件をすべて満たすノット シーケンスを選択する方法としては、最適なノットとして選択する方法、Gaffney/Powell の方法および Micchelli/Rivlin/Winograd の方法があります。
最適なノット
次のサイトにある値への "最適" なスプライン内挿では、
tau(1), ..., tau(n)
標準誤差式内の定数が最小となるようにノットを選択します。特に、最初と最後のデータ サイトは k 次のノットとして選択します。残りの n-k 個のノットは optknt で指定されます。
次に、optknt のヘルプの先頭部分を示します。
OPTKNT による最適なノット分布。
OPTKNT(TAU,K) returns an `optimal' knot sequence for
interpolation at data sites TAU(1), ..., TAU(n) by splines of
order K. TAU must be an increasing sequence, but this is not
checked.
OPTKNT(TAU,K,MAXITER) specifies the number MAXITER of iterations
to be tried, the default being 10.
The interior knots of this knot sequence are the n-K
sign-changes in any absolutely constant function h ~= 0 that
satisfies
integral{ f(x)h(x) : TAU(1) < x < TAU(n) } = 0
for all splines f of order K with knot sequence TAU.
OPTKNT の試行
例として、内挿用の optknt を使用して、3 次スプラインによるデータへの内挿を試みます。
(tau(i), y(i)), for i = 1, ..., n.
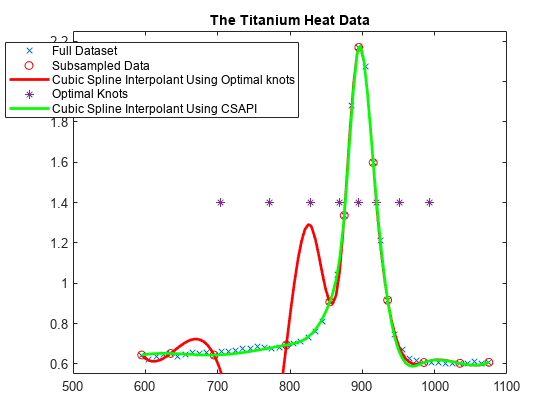
k = 4; osp = spapi( optknt(tau,k), tau,y); fnplt(osp,'r'); hl = legend({'Full Dataset' 'Subsampled Data' ... 'Cubic Spline Interpolant Using Optimal knots'}, ... 'location','NW'); hl.Position = hl.Position-[.14,0,0,0];
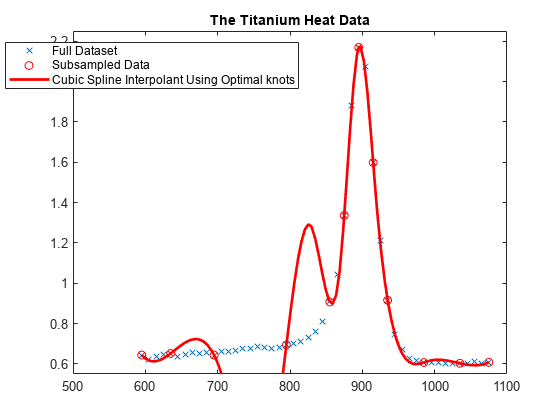
これには少し驚かされます。
次に、最適な内部ノットも星印で示します。
xi = fnbrk(osp,'knots'); xi([1:k end+1-(1:k)]) = []; plot(xi,repmat(1.4, size(xi)),'*'); hl = legend({'Full Dataset' 'Subsampled Data' ... 'Cubic Spline Interpolant Using Optimal knots' ... 'Optimal Knots'}, 'location','NW'); hl.Position = hl.Position-[.14,0,0,0];
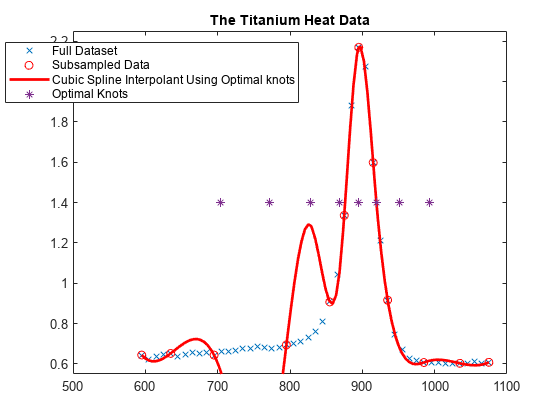
結果
最適な内挿のためのノットの選択は、次の割合の "すべて" の関数 f にわたって
norm(f - If) / norm(D^k f)
最大値ができる限り小さくなるように設計されています。ここで、分子は内挿誤差 f - If のノルム、分母は内挿 D^k f の k 番目の微分のノルムです。このデータは D^k f がかなり大きいことを意味しているため、データの平らな部分付近の内挿誤差は、このような '最適' スキームに受入可能なサイズとなります。
実際、これらのデータの場合は、csapi から提供される通常の 3 次スプライン内挿が非常にうまくいきます。
cs = csapi(tau,y); fnplt(cs,'g',2); hl = legend({'Full Dataset' 'Subsampled Data' ... 'Cubic Spline Interpolant Using Optimal knots' ... 'Optimal Knots' 'Cubic Spline Interpolant Using CSAPI'}, ... 'location','NW'); hl.Position = hl.Position-[.14,0,0,0]; hold off
最小二乗近似用のノットの選択
スプラインによる最小二乗近似を行う場合は、ノットを選択しなければなりません。1 つの方法としては、まず等間隔に配置したノットを使用し、次により最適なノット分布用に求めた近似に対して newknt を使用します。
以降のセクションでは、チタン熱データ セット全体を用いてこれらの手順について説明します。
一様のノット シーケンスによる最小二乗近似
一様のノット シーケンスから開始します。
unif = linspace(xx(1), xx(end), 2+fix(length(xx)/4)); sp = spap2(augknt(unif, k), k, xx, yy); plot(xx,yy,'x'); hold on fnplt(sp,'r'); axis([500 1100 .55 2.25]); title('The Titanium Heat Data'); hl = legend({'Full Dataset' ... 'Least Squares Cubic Spline Using Uniform Knots'}, ... 'location','NW'); hl.Position = hl.Position-[.14,0,0,0];
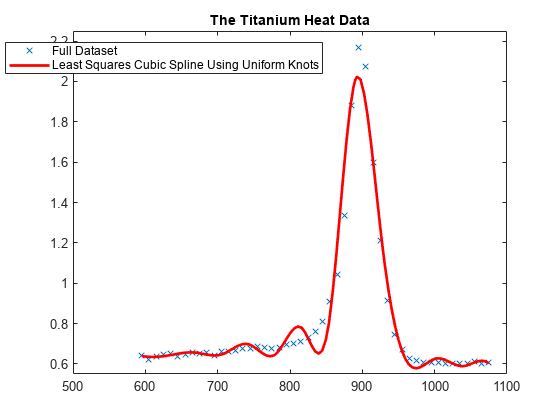
これはまったく満足できるものではありません。そこで、同じ次数および同じ多項式の項数で、ブレークの分布が改善されたスプライン近似に newknt を使用します。
NEWKNT を使用したノット分布の改善
spgood = spap2(newknt(sp), k, xx,yy); fnplt(spgood,'g',1.5); hl = legend({'Full Dataset' ... 'Least Squares Cubic Spline Using Uniform Knots' ... 'Least Squares Cubic Spline Using NEWKNT'}, ... 'location','NW'); hl.Position = hl.Position-[.14,0,0,0]; hold off
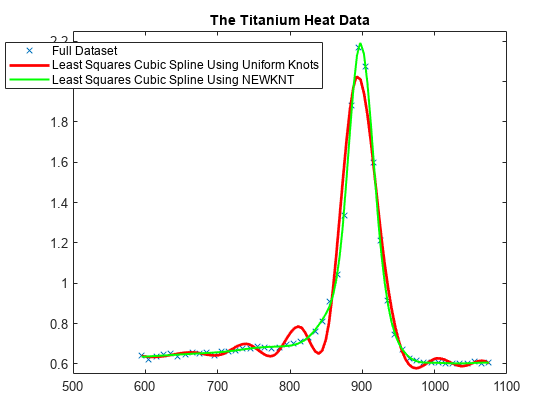
これはきわめて良好です。ちなみに、この場合は内部ノットの数が 1 個でも少なければ十分ではなかったでしょう。