3 次スプライン内挿
この例では、Curve Fitting Toolbox™ の csapi コマンドおよび csape コマンドを使用して、3 次スプライン内挿を作成する方法を示します。
CSAPI コマンド
以下のコマンドを入力します。
values = csapi(x,y,xx)
は、ノットなしの端点条件を使用して、与えられたデータ (x,y) に対する 3 次スプライン内挿の xx における値を返します。この内挿は、ブレーク シーケンス x をもつ区分的三次関数であり、その 3 次部分が結合して 2 つの連続状態変数の微係数をもつ関数を形成します。"ノットなし" の端点条件とは、最初と最後の内部ブレークで、3 階微分でも連続である (丸め誤差を除く) ことを意味します。
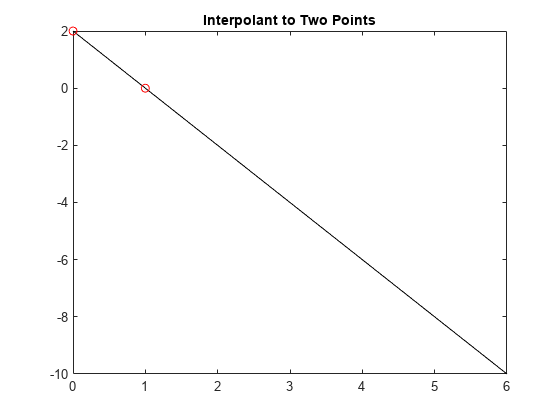
2 つのデータ点のみを指定すると、直線内挿になります。
x = [0 1]; y = [2 0]; xx = linspace(0,6,121); plot(xx,csapi(x,y,xx),'k-',x,y,'ro') title('Interpolant to Two Points')
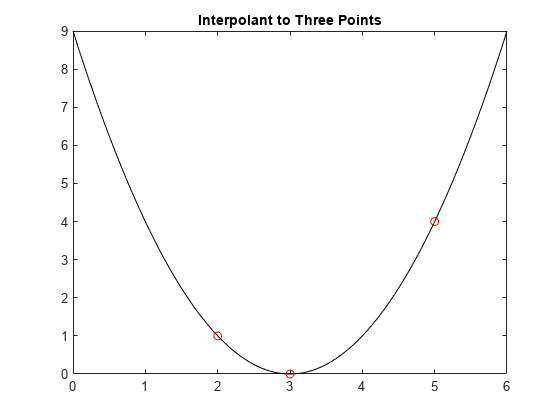
3 つのデータ点を指定すると、放物線が得られます。
x = [2 3 5]; y = [1 0 4]; plot(xx,csapi(x,y,xx),'k-',x,y,'ro') title('Interpolant to Three Points')
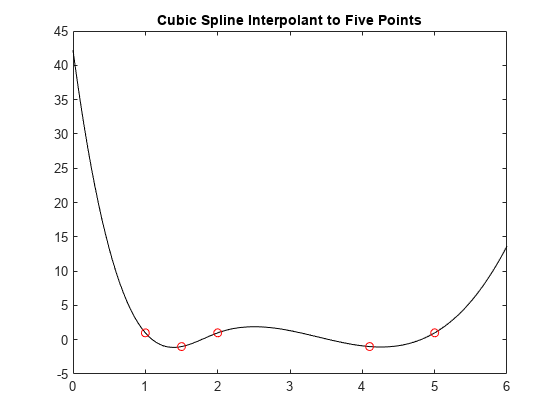
より一般的な例として、4 つ以上のデータ点を指定すると、3 次スプラインが得られます。
x = [1 1.5 2 4.1 5]; y = [1 -1 1 -1 1]; plot(xx,csapi(x,y,xx),'k-',x,y,'ro') title('Cubic Spline Interpolant to Five Points')
CSAPI の出力を確認する方法
これらの内挿は適切であるように見えますが、csapi の処理が説明どおりであるかをどのように確認すれば良いでしょうか。
データ点をプロットしたところ、内挿がこれらの点を正しく通っていたことから、csapi の内挿は既に確認できています。ただし、3 次スプラインが得られたことを確認するには、想定される種類の 3 次スプラインのデータから始め、csapi でその 3 次スプラインが "再現" されるかどうか、つまり、データの取得元である 3 次スプラインに戻るかどうかを確認するのが最善です。
例: 切断べき関数
3 次スプライン関数を確認する簡単な例としては、打ち切られた 3 のべき乗、つまり、次の関数があります。
ここで、xi はブレークの 1 つであり、添字の "+" はコマンド subplus で与えられる "切断関数" を示します。
help subplus subplus Positive part.
x , if x>=0
y = subplus(x) := (x)_{+} = ,
0 , if x<=0
returns the positive part of X. Used for computing truncated powers.
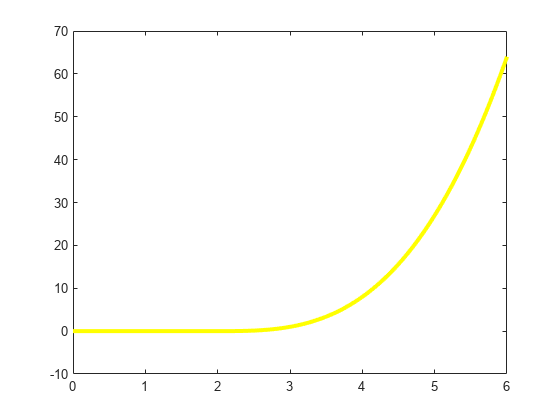
特定の選択肢 xi = 2 について、打ち切られた 3 のべき乗を次にプロットします。予想どおり、2 の左側は 0 であり、2 の右側は (x-2)^3 のように上昇しています。
plot(xx, subplus(xx-2).^3,'y','LineWidth',3) axis([0,6,-10,70])
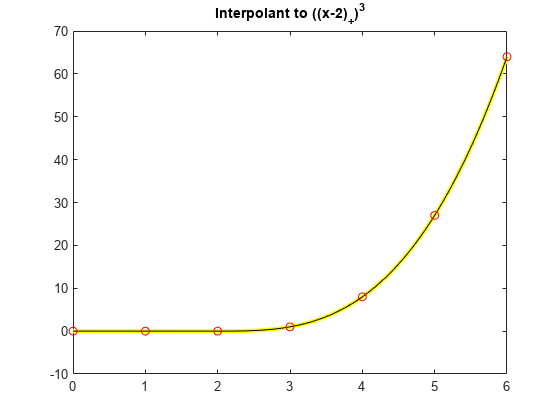
ここで、この特定の 3 次スプラインをデータ サイト 0:6 で内挿し、スプラインの上に内挿を黒でプロットします。
x = 0:6; y = subplus(x-2).^3; values = csapi(x,y,xx); hold on plot(xx,values,'k',x,y,'ro') hold off title('Interpolant to ((x-2)_+)^3')
内挿誤差
2 つの関数を比較する場合、通常はそれらの差異をプロットする方がはるかに多くの情報が得られます。
plot(xx, values - subplus(xx-2).^3)
title('Error in Cubic Spline Interpolation to ((x-2)_+)^3')
この差異の大きさを考慮に入れるため、最大データ値も計算します。これにより、この誤差がやむを得ない丸め誤差よりも悪くないことが示されます。
max_y = max(abs(y))
max_y = 64
打ち切られたべき乗を再現できない場合
追加のテストとして、csapi により生成されたサイト 0:6 の内挿が一致しない場合の打ち切られたべき乗を内挿します。たとえば、csapi は "ノットなし" 条件を使用するため、内挿スプラインの最初の内部ブレークは、実はノットではありません。そのため、この内挿はこのサイトで連続状態変数の微係数を 3 つもつことになります。つまり、その 3 階微分がそのサイトの周りでは不連続であるため、そのサイトを中心とする、打ち切られた 3 のべき乗を再現できないということになります。
values = csapi(x,subplus(x-1).^3,xx);
plot(xx, values - subplus(xx-1).^3)
title('Error in Not-a-Knot Interpolant to ((x-1)_+)^3')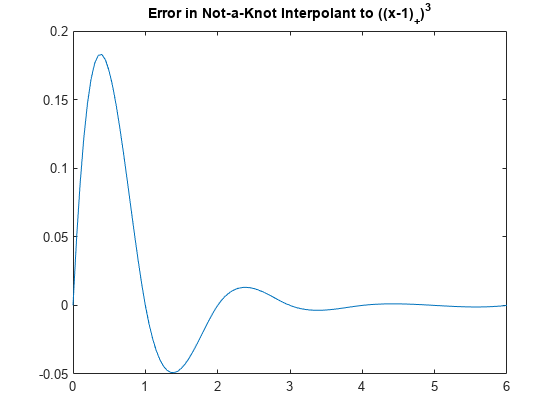
1 は最初の内部ノットであるため、この内挿ではアクティブではなくなります。
差の大きさは .18 ほどですが、1 から遠ざかるに従って減衰しています。これは、"3 次スプライン内挿が基本的に局所的" であることを説明しています。
値ではなく pp 型の使用
後での評価に適した形式、微分の計算に適した形式またはその他の操作に適した形式で、内挿 3 次スプラインを保持することができます。これは、次のような形式で csapi を呼び出すことで行います。
pp = csapi(x,y)
これは、内挿の pp 型を返します。この形式は、新しい点 xx で、次のコマンドによって評価できます。
values = fnval(pp,xx)
この内挿は、次のコマンドによって微分できます。
dpp = fnder(pp)
あるいは、次のコマンドで積分できます。
ipp = fnint(pp)
これらはそれぞれ、微分または積分の pp 型を返します。
例: 内挿の微分と積分
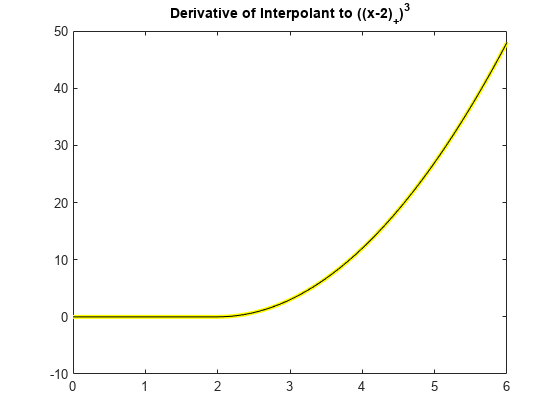
内挿の微分を示すため、次の打ち切られたべき乗の微分
をプロットします (ここでも黄色)。次に、その上に、元の 3 乗の切断べき関数に対する内挿の微分をプロットします (ここでも黒)。
plot(xx,3*subplus(xx-2).^2,'y','LineWidth',3) pp = csapi(x,subplus(x-2).^3); dpp = fnder(pp); hold on plot(xx,fnval(dpp,xx),'k') hold off title('Derivative of Interpolant to ((x-2)_+)^3')
繰り返しになりますが、差異をプロットする方が比較で多くの情報が得られます。また前回同様、これは丸め誤差と同じくらいの大きさです。
plot(xx, fnval(dpp,xx) - 3*subplus(xx-2).^2)
title('Error in Derivative of interpolant to ((x-2)_+)^3')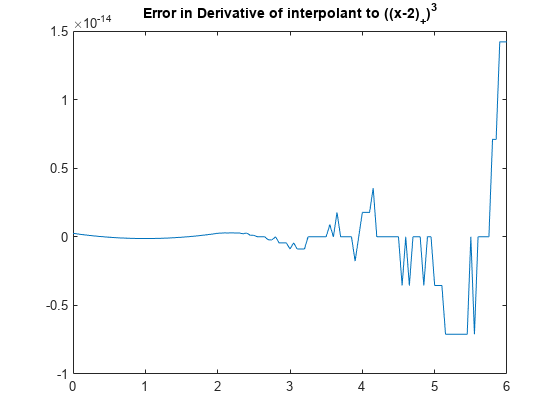
打ち切られたべき乗の 2 階微分は次のとおりです。
この関数と、元の関数に対する内挿の 2 階微分との間の差のプロットから、今度はジャンプがありますが、丸め誤差内に収まっていることが示されています。
ddpp = fnder(dpp);
plot(xx, fnval(ddpp,xx) - 6*subplus(xx-2))
title('Error in Second Derivative of Interpolant to ((x-2)_+)^3')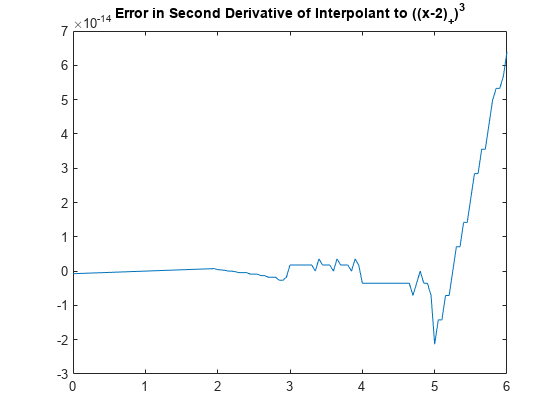
打ち切られたべき乗の積分は次のとおりです。
この関数と、元の関数に対する内挿の積分との間の差のプロットから、やはり誤差が丸め誤差内に収まっていることが示されています。
ipp = fnint(pp);
plot(xx, fnval(ipp,xx) - subplus(xx-2).^4/4)
title('Error in Integral of Interpolant to ((x-2)_+)^3')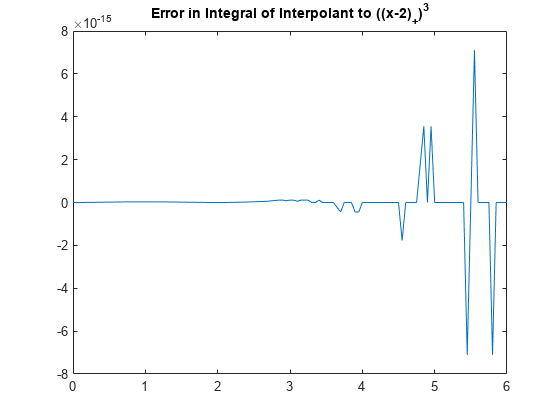
CSAPE コマンド
csapi と同様、csape コマンドは任意のデータに対する 3 次スプライン内挿を提供します。ただし、追加でさまざまな端点条件を指定できます。その最も単純なバージョンである
pp = csape(x,y)
はラグランジュ端点条件を使用します。これは、csapi で用いられるノットなし条件の代替手段によく使用されます。csape は内挿の値を直接返さず、pp 型のみを返します。
例として、次の関数に対する内挿を再度検討します。
これは、csapi でうまく再現されません。csape から求められる内挿の誤差 (赤) と共に、csapi によって返されるノットなし内挿の誤差 (黒) をプロットします。
exact = subplus(xx-1).^3; plot(xx, fnval(csapi(x,subplus(x-1).^3),xx) - exact,'k') hold on plot(xx, fnval(csape(x,subplus(x-1).^3),xx) - exact,'r') title('Error in Not-a-Knot vs. Lagrange End Conditions') legend({'Not-a-Knot' 'Lagrange'}); hold off

この場合、2 つの内挿にあまり差はありません。
その他の端点条件: '自然な' スプライン内挿
また、csape コマンドは、内挿 3 次スプラインのその他の種類の端点条件をいくつか指定する方法も提供します。たとえば、次のコマンド
pp = csape(x,y,'variational')
は、いわゆる '自然な' 端点条件を使用します。つまり、両端のブレークポイントで 2 階微分が 0 になります。
この手順では、'自然な' 3 次スプライン内挿を次の関数に適用し、
誤差をプロットする方法を示します。次のコードは、'variational' 引数に対応する別の引数構文を使用して '自然な' スプライン内挿を計算します。'second' により、csape が極値データ サイトで 2 階微分を既定値の 0 に設定することを指定します。
pp = csape(x,subplus(x-2).^3,'second'); plot(xx, fnval(pp,xx) - subplus(xx-2).^3) title('Error in ''Natural'' Spline Interpolation to ((x-2)_+)^3')
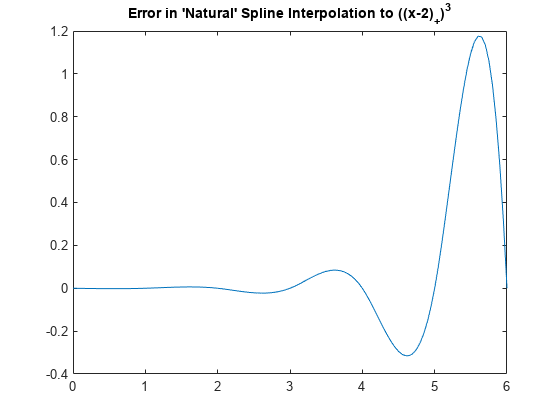
右端付近にある大きな誤差に注意してください。これは、'自然な' 端点条件がその位置でゼロの 2 階微分をもつことを暗黙的に示していることに起因します。
その他の端点条件: 2 階微分の指定
適切な 2 階微分を明示的に使用すると、誤差を小さくすることもできます。まず、打ち切られたべき乗の端点における適切な 2 階微分を計算します。
endcond = 6*subplus(x([1 end])-2);
次に、端点の 2 階微分が、計算した 2 階微分値と一致することを指定して、内挿を作成します。これは、データ値と共に、左の端点条件に endcond(1) を指定し、右に endcond(2) を指定して行います。
pp = csape(x,[endcond(1) subplus(x-2).^3 endcond(2)], 'second'); plot(xx, fnval(pp,xx) - subplus(xx-2).^3,'r') title(['Error in Spline Interpolation to ((x-1)_+)^3'; ... ' When Matching the 2nd Derivative at Ends '])
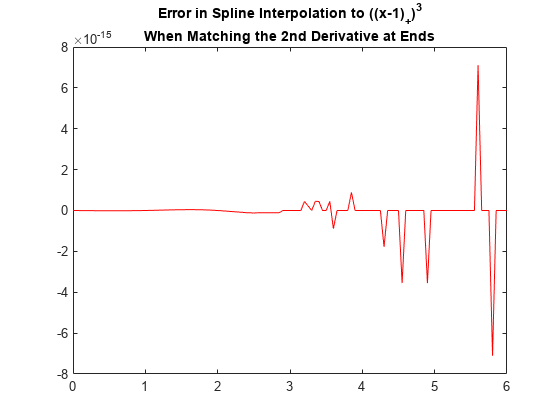
その他の端点条件: 傾きの指定
また、csape では端点の "傾き" を指定することもできます。これを "固定" (または "完全") 3 次スプライン内挿といいます。ステートメント
pp = csape(x,[sl,y,sr],'clamped')
によって、さらに左端のデータ サイトに傾き sl、右端のデータ サイトに傾き sr をもつデータ (x, y) への 3 次スプライン内挿を作成します。
その他の端点条件: 端点条件の混在
これまでの条件を混在させることも可能です。たとえば、前述の切断べき関数
では、x=0 で傾きが 0、x=6 で 2 階微分が 30 となります (最後のデータ サイト)。
そのため、左端の傾きと右端の曲率を一致させることで、結果の内挿に誤差がなくなることが予想されます。
pp = csape(x, [0 subplus(x-1).^3 30], [1 2]); plot(xx, fnval(pp,xx) - subplus(xx-1).^3) title(['Error in Spline Interpolation to ((x-1)_+)^3'; ... ' with Mixed End Conditions. '])
その他の端点条件: 周期的条件
"周期的な" 端点条件を指定することも可能です。たとえば、正弦関数の周期は 2*pi であり、サイト (pi/2)*(-2:2) における値は [0 -1 0 1 0] となります。正弦関数と、これらのサイトにおける周期的 3 次スプライン内挿との差異は 2 パーセントに過ぎません。これはまずまずの値です。
x = (pi/2)*(-2:2); y = [0 -1 0 1 0]; pp = csape(x,y, 'periodic' ); xx = linspace(-pi,pi,201); plot(xx, sin(xx) - fnval(pp,xx), 'x') title('Error in Periodic Cubic Spline Interpolation to sin(x)')
CSAPI または CSAPE で明示的にカバーされない端点条件
csape の既定周辺条件を用いた内挿を作成してから、これにゼロ値および一部の周辺条件への内挿の適切なスカラー倍を加算することで、csapi または csape で明示的にカバーされない端点条件を処理できます。2 つの '非標準' 周辺条件を満たす必要がある場合は、まず 2 行 2 列の線形システムを解かなければならない可能性があります。
たとえば、次のデータに対する 3 次スプライン内挿 s を計算するとします。
x = 0:.25:3; q = @(x) x.*(-1 + x.*(-1+x.*x/5)); y = q(x);
次の条件を適用します。
lambda(s) := a * (Ds)(e) + b * (D^2 s)(e) = c
これは点 e において s の 1 階微分および 2 階微分に対して行います。
このデータは、次の固有パラメーターをもつ周辺条件を満たす 4 次多項式から生成されます。
e = x(1); a = 2; b = -3; c = 4;
この固有条件を満たす内挿を作成するには、最初に作成する内挿が既定端点条件
pp1 = csape(x,y);
およびその最初の多項式区分の 1 階微分をもつようにします。
dp1 = fnder(fnbrk(pp1,1));
さらに、e において傾きが 1 となることを指定し、ゼロ データ値に対する 3 次スプライン内挿を作成します。
pp0 = csape(x,[1,zeros(size(y)),0], [1,0]);
また、その最初の多項式区分の 1 階微分も作成します。
dp0 = fnder(fnbrk(pp0,1));
次に、pp1 および pp0 の両方について lambda を計算します。
lam1 = a*fnval(dp1,e) + b*fnval(fnder(dp1),e); lam0 = a*fnval(dp0,e) + b*fnval(fnder(dp0),e);
pp1 および pp0 の適切な線形結合を作成し、次の 3 次スプラインを求めます。
s := pp1 + ((c - lambda(pp1))/lambda(pp0)) * pp0
これは目的の条件のほか、右の端点における既定の端点条件も満たしています。この線形結合は、fncmb を使用して形成します。
s = fncmb(pp0,(c-lam1)/lam0,pp1);
内挿誤差のプロットは、e 付近では、s による 4 次多項式の近似の方が、既定の条件を使用した内挿 pp1 よりも優れていることを示しています。
xx = (-.3):.05:.7; yy = q(xx); plot(xx, fnval(pp1,xx) - yy, 'x') hold on plot(xx, fnval(s,xx) - yy, 'o') hold off legend({'Default conditions' 'Nonstandard conditions'},'location','SE')

次の条件
mu(s) := (D^3 s)(3) = 14.6
を内挿の 3 階微分 (4 次式はこの条件を満たす) に対して適用する場合、左の端点における 1 階微分がゼロであり、そのため pp0 から確実に独立している状態で、ゼロ値に対する 3 次スプライン内挿を追加作成します。
pp2 = csape(x,[0,zeros(size(y)),1],[0,1]);
次に、次の線形結合の係数 d0 および d2 を求め、
s := pp1 + d0*pp0 + d2*pp2
線形システムを解きます。
lambda(s) = c
mu(s) = 14.6
pp0 および pp2 はどちらも、すべての内挿サイトで 0 になるため、s は選択したどの d0 および d2 についても任意のデータと一致することに注意してください。
試しに、MATLAB® エンコード機能で j=0:2 の場合の lambda(pp_j) および mu(pp_j) を計算するループを記述します。
dd = zeros(2,3); for j=0:2 J = num2str(j); eval(['dpp',J,'=fnder(pp',J,');']); eval(['ddpp',J,'=fnder(dpp',J,');']); eval(['dd(1,1+',J,')=a*fnval(dpp',J,',e)+b*fnval(ddpp',J,',e);']); eval(['dd(2,1+',J,')=fnval(fnder(ddpp',J,'),3);']); end
pp0、pp1 および pp2 の lambda と mu の値が得られたら、適切な線形結合を定義する係数の値を求めます。
d = dd(:,[1,3])\([c;14.6]-dd(:,2)); s = fncmb(fncmb(pp0,d(1),pp2,d(2)),pp1); xxx = 0:.05:3; yyy = q(xxx); plot(xxx, yyy - fnval(s,xxx),'x') title('Error in Spline Interpolant to y = x*(-1 + x*(-1+x*x/5))')

再確認のため、この関数に対する完全 3 次スプライン内挿で得られたものを使用してこの誤差を計算します。
hold on plot(xxx, yyy - fnval(csape(x,[-1,y,-7+(4/5)*27],'clamped'),xxx),'o') hold off legend({'Nonstandard conditions' 'Endslope conditions'})

この誤差は、終点付近でのみ (やや) 相違があり、pp0 および pp2 の両方がそれぞれの終点付近でのみ大きいという事実を示しています。
最終チェックとして、s が 3 における必要な 3 階微分条件を満たしていることを確認します。
fnval(fnder(s,3),3)
ans = 14.6000