信頼限界と予測限界

信頼限界と予測限界について

Curve Fitting Toolbox™ ソフトウェアでは、近似係数の信頼限界、新しい観測値または近似関数の予測限界を計算できます。さらに、予測限界については、すべての予測子値を考慮する同時限界または個々の予測子値のみを考慮する非同時限界を計算できます。係数の信頼限界は数値的に表されますが、予測限界はグラフィカルに表示されると共に数値的に使用することもできます。

使用可能な信頼限界と予測限界を以下にまとめます。

信頼限界と予測限界のタイプ

区間のタイプ	説明
近似係数	近似係数の信頼限界
新しい観測値	新しい観測値 (応答値) の予測限界
新しい関数	新しい関数値の予測限界

メモ:

予測された応答の信頼区間を計算するため、予測限界は信頼限界と呼ばれる場合もあります。

信頼限界と予測限界は、関連する区間の下限値と上限値を定義し、区間の幅を定義します。区間の幅は、近似係数、予測された観測値または予測された近似についての不確かさの程度を示します。たとえば、近似係数の区間が非常に広い場合は、係数について具体的な判断をする前に、より多くのデータを使用して近似する必要がある可能性を示しています。

範囲は、指定した確かさの程度で定義されます。確かさの程度は多くの場合 95% ですが、90%、99%、99.9% など任意の値を使用できます。たとえば、新しい観測値の予測に不正確な値が発生する可能性を 5% とすることができます。この場合は、95% の予測区間を計算します。この区間は、新しい観測値が予測限界の上限と下限の間に実際に含まれる可能性が 95% であることを示します。

係数の信頼限界

近似係数の信頼限界は次で与えられます。

$C = b \pm t \sqrt{S}$

ここで、b は近似によって生成される係数、t は信頼水準に依存し、スチューデントの累積分布関数 t の逆関数を使用して計算されます。S は、係数推定値についての推定共分散行列 (X^TX)^–1s² の対角要素のベクトルです。線形近似では X は計画行列ですが、非線形近似では X は係数についての近似値のヤコビアンです。X^T は X の転置行列であり、s² は平均二乗誤差です。

信頼限界は曲線フィッターアプリで確認できます。アプリの [結果] ペインにある [係数と 95% 信頼限界] テーブルに範囲が表示されます。

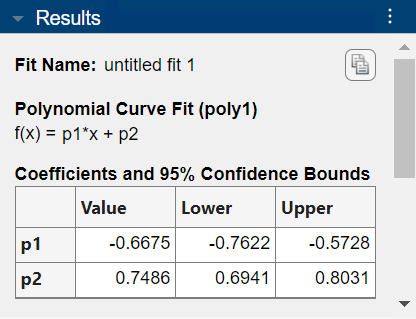
Results pane showing the Coefficients and 95% Confidence Bounds table

係数 p1 の近似値は -0.6675、下限は -0.7622、上限は -0.5728 です。

関数 confint を使用して、コマンドラインで信頼区間を計算できます。

近似の予測限界

前述のように、近似曲線の予測限界を計算できます。この予測はデータの既存の近似に基づいています。さらに、範囲には、すべての予測子値の信頼性を測定する同時限界、または事前に決めた単一の予測子値のみの信頼性を測定する非同時限界があります。新しい観測値を予測している場合、非同時限界は、指定した単一の予測子値に対して新しい観測値が区間内に入る信頼性を測定します。同時限界は、予測子値に関係なく新しい観測値が区間内に入る信頼性を測定します。

範囲のタイプ	観測値	関数
同時	$y \pm f \sqrt{s^{2} + x S x^{T}}$	$y \pm f \sqrt{x S x^{T}}$
非同時	$y \pm t \sqrt{s^{2} + x S x^{T}}$	$y \pm t \sqrt{x S x^{T}}$

範囲のタイプ

観測値

関数

同時

$y \pm f \sqrt{s^{2} + x S x^{T}}$

$y \pm f \sqrt{x S x^{T}}$

非同時

$y \pm t \sqrt{s^{2} + x S x^{T}}$

$y \pm t \sqrt{x S x^{T}}$

ここで、

s² は平均二乗誤差です。
t は信頼水準に依存し、スチューデントの累積分布関数 t の逆関数を使用して計算されます。
f は信頼水準に依存し、累積分布関数 F の逆関数を使用して計算されます。
S は係数推定値の共分散行列 (X^TX)^–1s² です。
x は、指定した予測子値で評価した計画行列またはヤコビアンの行ベクトルです。

曲線フィッターアプリを使用して予測限界をグラフィカルに表示できます。曲線フィッターアプリでは、新しい観測値の非同時予測限界を表示できます。[曲線フィッター] タブの [可視化] セクションで、[予測範囲] リストから確かさのレベルを選択します。このレベルを任意の値に変更するには、リストから [カスタム] を選択します。

コマンドラインで関数 predint を使用すると、任意のタイプの予測限界を数値的に表示できます。

それぞれのタイプの予測区間に関連する数量を理解するには、データ、近似および残差が次の式で関連していることを思い出してください。

"データ" = "近似" + "残差"

ここで、近似と残差の項は、次の式の各項の推定値です。

"データ" = "モデル" + "確率的誤差"

予測子値 x_n+1 で新しい観測値を取得するとします。新しい観測値を y_n+1(x_n+1)、関連する誤差を ε_n+1 とします。この場合

y_n+1(x_n+1) = f(x_n+1) + ε_n+1

ここで、f(x_n+1) は、x_n+1 で推定する真であるが未知の関数です。新しい観測値または推定関数の可能性の高い値は非同時予測限界によって与えられます。

一方、任意の予測子値に関連する新しい観測値の可能性の高い値が必要な場合、前の方程式は次のようになります。

y_n+1(x) = f(x) + ε

この新しい観測値または推定関数の可能性の高い値は同時予測限界によって与えられます。

予測限界のタイプを以下にまとめます。

予測限界のタイプ

範囲のタイプ	同時または非同時	関連する方程式
観測値	非同時	y_n+1(x_n+1)
観測値	同時	y_n+1(x) (すべての x について)
関数	非同時	f(x_n+1)
関数	同時	f(x) (すべての x について)

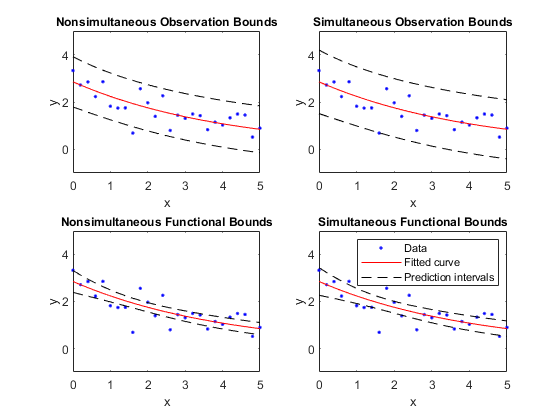
新しい観測値および近似関数の同時予測限界と非同時予測限界を次に示します。各グラフには、近似、信頼限界の下限、信頼限界の上限の 3 つの曲線が含まれています。この近似は、生成データについての単項指数関数であり、範囲は 95% の信頼水準を反映しています。新しい応答値の予測では不確定性が追加されるため (曲線プラス確率的誤差)、新しい観測値に関係する区間は近似関数の区間よりも広くなることに注意してください。

Plots of different types of bounds

コマンドラインからの予測区間の計算

ライブスクリプトを開く

ノイズデータの近似について観測値と関数の予測区間を計算しプロットします。

指数関数的トレンドのノイズを含むデータを生成します。

x = (0:0.2:5)';
y = 2*exp(-0.2*x) + 0.5*randn(size(x));

単項指数関数を使用して曲線をデータに当てはめます。

fitresult = fit(x,y,'exp1');

同時と非同時の両方について観測値と関数の 95% 予測区間を計算します。非同時限界は x の個々の要素に対応し、同時限界は x のすべての要素に対応します。

p11 = predint(fitresult,x,0.95,'observation','off');
p12 = predint(fitresult,x,0.95,'observation','on');
p21 = predint(fitresult,x,0.95,'functional','off');
p22 = predint(fitresult,x,0.95,'functional','on');

データ、近似および予測区間をプロットします。新しい観測値のランダムな変動に加え、近似曲線の予測における不確定性が測定されるため、観測値の範囲は関数の範囲より広くなります。

subplot(2,2,1)
plot(fitresult,x,y), hold on, plot(x,p11,'m--'), xlim([0 5]), ylim([-1 5])
title('Nonsimultaneous Observation Bounds','FontSize',9)
legend off
   
subplot(2,2,2)
plot(fitresult,x,y), hold on, plot(x,p12,'m--'), xlim([0 5]), ylim([-1 5])
title('Simultaneous Observation Bounds','FontSize',9)
legend off

subplot(2,2,3)
plot(fitresult,x,y), hold on, plot(x,p21,'m--'), xlim([0 5]), ylim([-1 5])
title('Nonsimultaneous Functional Bounds','FontSize',9)
legend off

subplot(2,2,4)
plot(fitresult,x,y), hold on, plot(x,p22,'m--'), xlim([0 5]), ylim([-1 5])
title('Simultaneous Functional Bounds','FontSize',9)
legend({'Data','Fitted curve', 'Prediction intervals'},...
       'FontSize',8,'Location','northeast')

曲線フィッターアプリを使用した予測限界の計算

ライブスクリプトを開く

census データセットを読み込みます。

load census

変数 cdate と pop には、国勢調査が実施された日付と人口のデータが含まれています。

曲線フィッターアプリを開きます。

curveFitter

アプリで、近似のデータ変数を選択します。[曲線フィッター] タブの [データ] セクションで [データの選択] をクリックします。[近似データの選択] ダイアログボックスで、[X データ] の値として cdate、[Y データ] の値として pop を選択します。

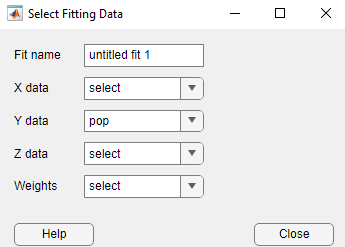
変数を選択すると、アプリによってデータ点がプロットされます。

国勢調査データとデータの線形近似がプロットに表示されます。

近似の 95% 予測限界をプロットします。[曲線フィッター] タブの [可視化] セクションにある [予測範囲] で [95%] を選択します。

国勢調査データと線形近似に加えて、95% 予測区間がプロットに表示されます。

近似の 60% 予測限界をプロットするには、カスタムの信頼水準を指定する必要があります。[曲線フィッター] タブの [可視化] セクションにある [予測範囲] で [カスタム] を選択します。[予測範囲の設定] ダイアログボックスで、[信頼水準 (%)] ボックスに「60」と入力し、[OK] をクリックします。

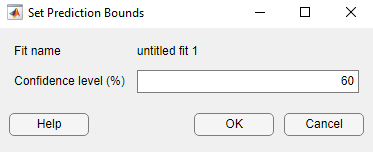
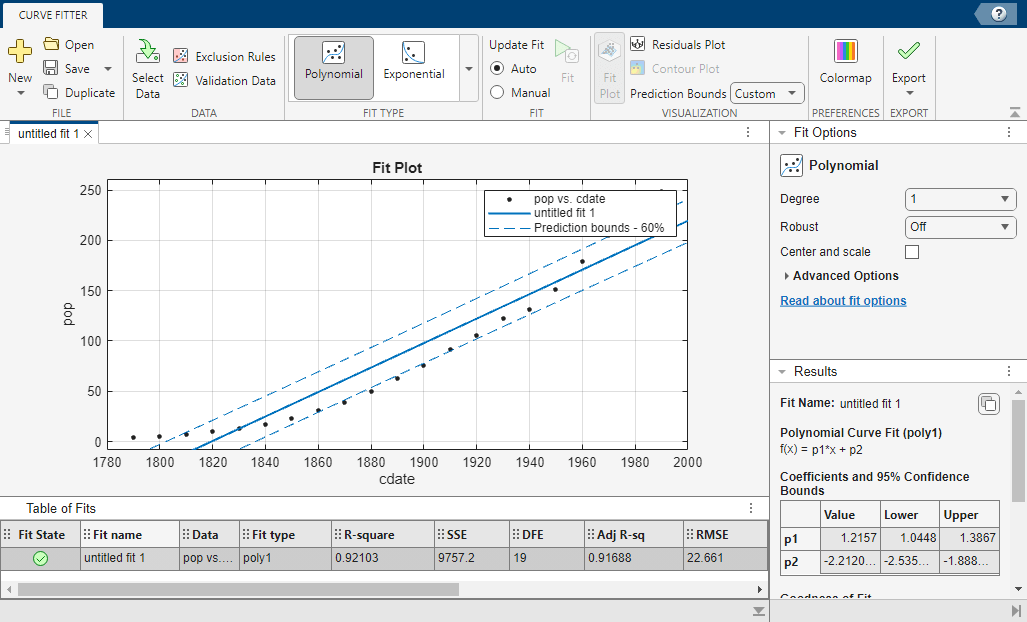
国勢調査データと線形近似に加えて、60% 予測区間がプロットに表示されます。2 つのプロットをまとめて考えると、60% 予測区間の方が 95% 予測区間よりも線形近似に近いことがわかります。