モデルの離散化とリサンプリング
この例では、連続/離散、離散/連続、離散/離散の変換に用いるコマンドの使用方法を示します。
関連コマンド
Control System Toolbox™ には、線形システムの離散化とリサンプリングのための豊富なサポートが用意されています。以下はその例です。
c2dは連続時間モデルを離散化d2cは離散時間モデルから連続時間モデルへの変換を計算d2dは離散時間モデルをリサンプリング
これらの操作は、以下のアルゴリズムを使用して実行できます。
ゼロ次ホールド
1 次ホールド
インパルス不変法
双一次 (Tustin) 変換
極と零点マッチング法

連続/離散の変換
たとえば、遅延を含む 2 次システムがあるとします。

サンプリング レート 10 Hz を使用して、このシステムのゼロ次ホールド (ZOH) 離散化を計算するには、次のように入力します。
G = tf([1 -2],[1 3 20],'inputdelay',1); Ts = 0.1; % sampling interval Gd = c2d(G,Ts)
Gd =
0.07462 z - 0.09162
z^(-10) * ----------------------
z^2 - 1.571 z + 0.7408
Sample time: 0.1 seconds
Discrete-time transfer function.
連続ステップ応答と離散ステップ応答を比較します。
step(G,'b',Gd,'r') legend('Continuous','Discretized')

離散/連続の変換
逆に d2c を使用すると、特定の離散時間システムの連続時間 "内挿" を計算できます。上記で計算した離散化 Gd から開始し、連続時間に再変換して、元のモデル G と比較します。
Gc = d2c(Gd); step(G,'b',Gd,'r',Gc,'g--') legend('Original','Discretized','D2C Interpolant')
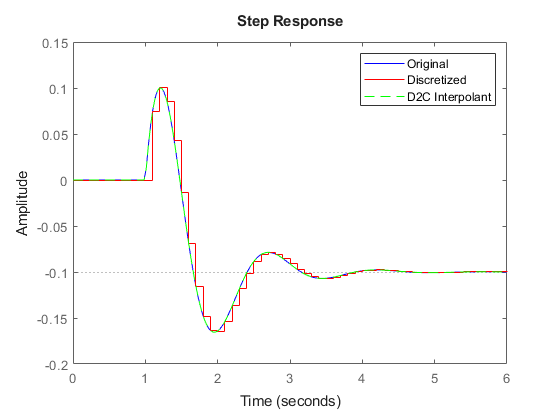
2 つの連続時間応答は完全に一致します。サンプリング間隔 Ts が大きすぎて離散化時にエイリアシングが発生する場合は特に、完全一致が必ず得られるとは限りません。
Ts = 1; % 10 times larger than previously Hd = c2d(G,Ts); Hc = d2c(Hd); step(G,'b',Hd,'r',Hc,'g--',10) legend('Original','Discretized','D2C Interpolant')

離散時間システムのリサンプリング
リサンプリングは、離散時間システムのサンプリング間隔を変更することによって行われます。この操作は d2d を使用して実行されます。たとえば、元の連続時間モデル G の 10 Hz 離散化 Gd について考えます。次のコマンドを使用すると、この離散化を 40 Hz でリサンプリングできます。
Gr = d2d(Gd,0.025)
Gr =
0.02343 z - 0.02463
z^(-40) * ----------------------
z^2 - 1.916 z + 0.9277
Sample time: 0.025 seconds
Discrete-time transfer function.
これを 40 Hz の直接離散化と比較します。
step(G,'b',Gr,'r',c2d(G,0.025),'g--',4) legend('Continuous','Resampled from 0.1 to 0.025','Discretized with Ts=0.025')
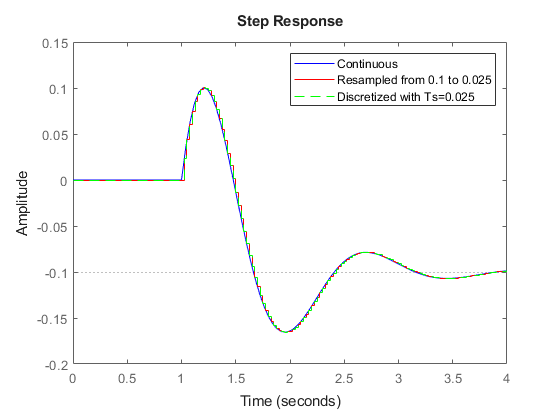
どちらのアプローチからも同じ答えが得られます。
どのアルゴリズムとサンプリング レートを選択すべきか
アルゴリズムとサンプリング レートの選択内容が離散化の精度に与える影響の詳細については、ノッチ フィルターの離散化の例を参照してください。