このページは機械翻訳を使用して翻訳されました。最新版の英語を参照するには、ここをクリックします。
ゾーン調和重力モデルと他の重力モデルの比較
この例では、地球の表面の +/- 90 度の緯度に対するゾーン調和重力モデル、球面重力モデル、および 1984 年世界測地系 (WGS84) 重力モデルを調べる方法を示します。
地球中心地球固定(ECEF)位置を決定する
ECEF 座標系は地心座標系であるため、球面方程式を使用して地心緯度、経度、地心半径から位置を決定できます。
geocradius を使用して、+/- 90 度の緯度配列における地心半径をメートル単位で計算します。
lat = -90:90; r = geocradius( lat ); rlat = convang( lat, 'deg', 'rad'); z = r.*sin(rlat);
経度は帯状調和重力モデルには影響しないため、y 位置はゼロであると想定します。
x = r.*cos(rlat); y = zeros(size(x));
地球の帯状調和重力を計算する
gravityzonal を使用して、ECEF 位置入力の配列に対して、ECEF 座標系のゾーン調和重力成分をメートル/秒の二乗で計算します。
[gx_zonal, gy_zonal, gz_zonal] = gravityzonal([x' y' z']);
WGS84重力を計算する
gravitywgs84 を使用して、地球表面の下軸と北軸の WGS84 重力を計算します。WGS84 重力は、大気、遠心力の影響、歳差運動のない正確な方法を使用して計算された測地緯度 (度) と経度 0 度の配列です。
lat_gd = geoc2geod(lat, r);
long_gd = zeros(size(lat));
[gd_wgs84, gn_wgs84] = gravitywgs84( zeros(size(lat)), lat_gd, long_gd, 'Exact', [false true false 0] );球状の地球の重力を決定する
地球の重力パラメータ(立方メートル毎秒の二乗)を使用して、地心半径(メートル毎秒の二乗)の配列に対する質点重力の配列を計算します。
GM = 3.986004415e14; gd_sphere = -GM./(r.*r);
異なる重力モデルの比較図
重力モデルを比較するには、それらの出力が同じ座標系にある必要があります。dcmecef2ned の方向余弦行列を使用して、ゾーン重力を ECEF 座標から NED 座標に変換できます。
dcm_ef = dcmecef2ned( lat_gd, long_gd ); gxyz_zonal = reshape([gx_zonal gy_zonal gz_zonal]', [3 1 181]); gned_zonal = squeeze(pagemtimes(dcm_ef,gxyz_zonal))'; figure(1) plot(lat_gd, gned_zonal(:,3), lat, -gd_sphere, '--', lat_gd, gd_wgs84, '-.') legend('Zonal Harmonic', 'Point-mass', 'WGS84','Location','North') xlabel('Geodetic Latitude (degrees)') ylabel('Down gravity (m/s^2)') grid on

図 1: 下軸の重力(メートル毎秒二乗)
figure(2) plot( lat_gd, gned_zonal(:,1), [lat(1) lat(end)], [0 0], '--', lat_gd, gn_wgs84, '-.'); legend('Zonal Harmonic', 'Point-mass', 'WGS84','Location','Best') xlabel('Geodetic Latitude (degrees)') ylabel('North gravity (m/s^2)') grid on hold off

図 2: 北軸の重力(メートル毎秒二乗)
WGS84 の全重力とゾーン重力ベクトルをメートル毎秒の二乗で計算します。
gtotal_wgs84 = gravitywgs84( zeros(size(lat)), lat_gd, zeros(size(lat)), 'Exact', [false true false 0] );
gtotal_zonal = sqrt(sum([gx_zonal.^2 gy_zonal.^2 gz_zonal.^2],2));figure(3) plot( lat, gtotal_zonal, lat_gd, gtotal_wgs84, '-.' ) legend('Zonal Harmonic', 'WGS84','Location','North') xlabel('Geodetic Latitude (degrees)') ylabel('Total gravity (m/s^2)') grid on

図 3: 総重力(メートル毎秒二乗)
遠心力の影響を考慮した重力モデルの比較
さて、回転していない地球の重力の比較を見てきました。地球の自転による遠心力が重力モデルに及ぼす影響を調べます。
地球の重力遠心力効果を計算する
gravitycentrifugal を使用して、ECEF 位置の配列 (メートル毎秒の二乗単位) の ECEF 座標における遠心効果の配列を計算します。
[gx_cent, gy_cent, gz_cent] = gravitycentrifugal([x' y' z']);
ゾーン調和重力に遠心効果を追加します。
gx_cent_zonal = gx_zonal + gx_cent; gy_cent_zonal = gy_zonal + gy_cent; gz_cent_zonal = gz_zonal + gz_cent;
遠心力の影響を考慮したWGS84重力を計算する
gravitywgs84 を使用して、地球表面の下軸と北軸の WGS84 重力を計算します。WGS84 重力は、大気、遠心力の影響、歳差運動のない正確な方法を使用して計算された測地緯度 (度) と経度 0 度の配列です。
[gd_cent_wgs84, gn_cent_wgs84] = gravitywgs84( zeros(size(lat)), lat_gd, long_gd, 'Exact', [false false false 0] );WGS84 の遠心効果を考慮した総重力と、メートル毎秒の二乗単位のゾーン重力ベクトルを計算します。
gtotal_cent_wgs84 = gravitywgs84( zeros(size(lat)), lat_gd, zeros(size(lat)), 'Exact', [false false false 0] );
gtotal_cent_zonal = sqrt(sum([gx_cent_zonal.^2 gy_cent_zonal.^2 gz_cent_zonal.^2],2));遠心力の影響を考慮した異なる重力モデルの比較図
重力モデルを比較するには、それらの出力が同じ座標系にある必要があります。dcmecef2ned の方向余弦行列を使用して、ゾーン重力を ECEF 座標から NED 座標に変換できます。図 5 では、遠心効果のある帯状調和重力と遠心効果のある WGS84 重力の間に若干の違いがあることがわかります。違いのほとんどは、帯状調和重力計算と WGS84 重力計算の違いによるものです。
gxyz_cent_zonal = reshape([gx_cent_zonal gy_cent_zonal gz_cent_zonal]', [3 1 181]); gned_cent_zonal = squeeze(pagemtimes(dcm_ef,gxyz_cent_zonal))'; figure(4) plot(lat_gd, gned_cent_zonal(:,3), lat_gd, gd_cent_wgs84, '-.') legend('Zonal Harmonic', 'WGS84','Location','North') xlabel('Geodetic Latitude (degrees)') ylabel('Down gravity (m/s^2)') grid on

図 4: 下軸における遠心力の影響による重力(メートル毎秒二乗)
figure(5) plot( lat_gd, gned_cent_zonal(:,1), lat_gd, gn_cent_wgs84, '--', lat_gd, (gned_zonal(:,1)-gn_wgs84'), '-.' ) axis([-100 100 -0.0002 0.0002]) legend('Zonal Harmonic', 'WGS84', 'Error Between Models w/o Centrifugal Effects', 'Location','Best') xlabel('Geodetic Latitude (degrees)') ylabel('North gravity (m/s^2)') grid on

図 5: 北軸の重力(メートル毎秒二乗)
figure(6) plot( lat, gtotal_cent_zonal, lat_gd, gtotal_cent_wgs84, '-.' ) legend('Zonal Harmonic', 'WGS84','Location','North') xlabel('Geodetic Latitude (degrees)') ylabel('Total gravity (m/s^2)') grid on
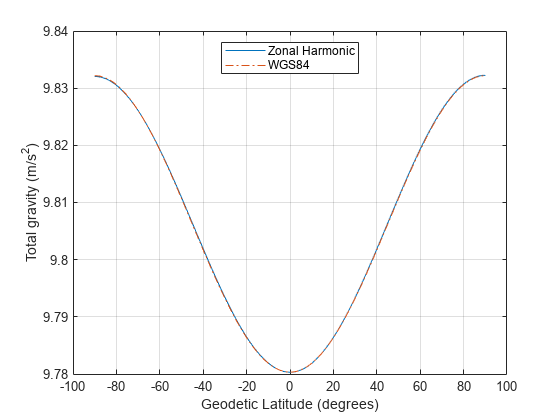
図 6: 遠心力の影響を含む総重力(メートル毎秒2乗)