このページは機械翻訳を使用して翻訳されました。最新版の英語を参照するには、ここをクリックします。
国際宇宙ステーションの高精度軌道伝播
この例では、Aerospace Blockset ™ を使用した高精度数値軌道伝播を使用して、国際宇宙ステーション (ISS) の軌道を伝播する方法を示します。Orbit Propagator ブロックを使用して、ISS の 24 時間の軌道を計算します。次に、この例では、位置と速度の状態を、ジョンソン宇宙センターの NASA 軌道運用および計画 (TOPO) フライト コントローラーから入手できる公開 ISS 軌道データと比較します。
Orbit Propagator ブロックは、数値積分を使用して宇宙機の並進ダイナミクスをモデル化します。時間の経過に伴う 1 つまたは複数の宇宙機の位置と速度を計算します。最も正確な結果を得るには、許容誤差設定が低い (1e-9 未満) 可変ステップ ソルバーを使用します。ミッションの要件に応じて、より大きな許容値を使用することでシミュレーションの実行時間を短縮できます。そうすると、ソリューションの精度に影響する可能性があります。軌道状態を伝播するために、ブロックは現在の中心天体に対して選択された重力モデルを使用します。このブロックには、大気抵抗(地球軌道の場合)、中心天体以外の天体の重力の影響、太陽放射圧も含まれます。このブロックは、ブロックへの入力として提供される外部摂動加速度も考慮します。
この例では、参照されているNASAの公開配布ファイル[1]からISS国際天体基準フレーム(ICRF)の位置と速度の状態を直接使用して、Orbit PropagatorブロックでISS軌道を初期化します。EGM2008 球面調和重力モデルを使用して地球の重力をモデル化し、NRLMSISE-00 大気モデルを使用して、宇宙天気 (太陽フラックスと地磁気指数) が大気密度に与える影響を含め、大気抵抗を計算します。月、太陽、木星の第三天体の重力質点の寄与を計算します。最後に、球形の衛星形状を想定して、太陽放射圧 (SRP) の影響を考慮します。ISS のような低地球軌道では、第三天体の重力と太陽放射圧による摂動はほぼ無視できます。ただし、高精度の軌道伝播に可能な構成を示すために、この例にはそれらが含まれています。正確な軌道モデリングに必要な摂動は、アプリケーションと軌道領域によって異なります。ミッションに応じて、ケースバイケースでどの摂動を含めるかを決定します。
モデルを 24 時間実行し、公開されている NASA の軌道データと比較します。
ミッションの初期条件を設定する
この例では、MATLAB ® 構造を使用してミッション データを整理します。これらの構造により、例の後半でのデータへのアクセスがより直感的になります。また、グローバル ベース ワークスペースの整理にも役立ちます。
NASAが提供する参照ISSエフェメリスデータファイル[1]は、2022年1月3日12:00:00.000 UTCから始まります。
mission.StartDate = datetime(2022, 1, 3, 12, 0, 0); mission.Duration = hours(24);
ファイルには、4 分ごとにサンプリングされた ICRF 位置 (km) と速度 (km/s) のデータが含まれています。
iss.X0_icrf = [-1325.896391725290 5492.890955896010 3762.423747679220]; % km iss.V0_icrf = [-4.87470128630892 -4.10251688094599 4.26428812476909]; % km/s
また、エポックに対応する質量 (kg)、抗力面積 (m^2)、抗力係数データも含まれています。
iss.Mass = 459023.0; % kg iss.DragArea = 1951.0; % m^2 iss.DragCoeff = 2.0;
ファイルには太陽放射面積 (m^2) と太陽放射係数も含まれていますが、ISS が動作する低軌道 (LEO) では SRP が顕著ではないため、これらの値はゼロになります。結果として得られる軌道への影響はわずかですが、高精度の軌道伝播を完全に実証するために、この例では太陽放射圧の計算を含めます。SRP はより高い軌道領域でより顕著になります。
iss.SRPArea = 1500; % m^2 iss.SRPCoeff = 1.8; iss.P_sr = 4.5344321e-6; % N/m^2
高精度軌道伝播アルゴリズム
Orbit Propagator ブロックは、Cowell 法を使用して高精度の数値軌道伝播を実行します。慣性 (ICRF) フレームでのシミュレーションの各タイム ステップでの位置と速度を計算するために、地球の重力加速度がすべての摂動加速度と合計され、二重積分されます。
ここで、
は地球の重力による加速度です。
は大気抵抗による加速度です。
は、月、太陽、および太陽系の惑星の重力による加速度です。含める第 3 の天体の正しいリストは、中心天体、軌道、およびアプリケーションによって異なります。
は太陽放射圧による加速度です。
地球の重力
この例の地球の重力モデルは、EGM2008 球面調和重力モデルです。このモデルは、ゾーン、セクター、テッセラルの高調波を考慮します。参考までに、地球の扁平率を説明する 2 次ゼロ次帯状調和関数 は です。球面調和関数モデルは、最大次数 までの高調波を考慮します。EGM2008の場合は、。
球面調和重力は、固定フレーム (ff) 座標系 (地球の場合は国際地球基準フレーム (ITRF)) で計算されます。ただし、数値積分は常に慣性 ICRF 座標系で実行されます。したがって、各タイムステップで、位置と速度の状態が固定フレームに変換され、重力が固定フレームで計算され、結果として得られる加速度が慣性フレームに変換されます。
ここで、
球座標における次の偏微分が与えられます。
はルジャンドル関数です。
と は正規化されていない調和係数です。
大気抵抗
Orbit Propagator ブロックは、NRLMSISE-00 大気モデルを使用して大気抵抗による加速の組み込みをサポートします。大気抵抗は LEO における主要な摂動であり、軌道操作の支援がなければ、時間の経過とともに ISS の軌道が低下します。
大気抵抗は次のように計算されます。
ここで、
は大気の密度です。
は宇宙機の抗力係数です。
は宇宙機の抗力領域、つまり に垂直な領域です。
は宇宙機の質量です。
は大気に対する宇宙機の速度です。
NRLMSISE-00 大気モデルは、大気密度を計算するために使用されます。これには宇宙天気データ (F10.7 および F10.7A の電波フラックス値と地磁気指数) が必要ですが、これは CelesTrak® から統合形式で取得できます。MATLAB および Simulink ® の宇宙天気データの詳細については、Solar Flux and Geomagnetic Index ブロックのリファレンス ページと Aerospace Toolbox aeroReadSpaceWeatherData 関数のリファレンス ページを参照してください。
第三の重力
3 番目の天体の重力は、月、太陽、太陽系のすべての惑星、または任意の数のカスタム天体の Orbit Propagator ブロックに含めることができます。各天体の重力は次のように計算されます(太陽の場合)。
ここで、
は太陽の重力パラメータです。
は、JPL DE405 惑星エフェメリス データに基づく、宇宙機から太陽の中心へのベクトルです。惑星の暦の詳細については、Planetary Ephemeris ブロックのリファレンス ページまたは Aerospace Toolbox planetEphemeris 関数のリファレンス ページをご覧ください。
は、JPL DE405 エフェメリス データに基づく、地球の中心から太陽の中心へのベクトルです。
太陽放射圧
太陽放射圧は LEO の軌道伝播にほとんど影響を与えません。ただし、この例では完全性を保つためにこれらの計算が含まれています。Orbit Propagator ブロックは太陽放射圧を次のように計算します。
ここで、
は影の割合です。値は次のいずれかになります。
umbraでは0に等しい
半影または前影で0から1の間
1(完全な日光)に等しい
ミッションの要件に応じて、ブロックでは忠実度の異なる 2 つの日食モデルがサポートされます。
デュアルコーンシャドウモデルは、宇宙機の位置から見える太陽ディスクの割合を計算します。これは部分日食、金環日食、皆既日食を区別するもので、宇宙機が日光、半影、前影、または本影のいずれの領域にあるかを意味します。日食は、半影では部分日食、前影では環状日食、本影では皆既日食となります。
円筒影モデルでは、太陽が掩蔽天体や宇宙機から無限に離れており、太陽光線はすべて平行であると仮定します。この場合、宇宙機は直射日光下にあるか、本影の中にあります。影の割合は 0 または 1 のみになります。
は反射係数です。
は宇宙機の SRP 領域、つまり太陽から見た断面積です。
は宇宙機の質量です。
は太陽から 1AU の距離における太陽放射圧です。
は太陽から地球までの平均距離(1 AUに等しい)
は、JPL エフェメリス データに基づく、宇宙機から太陽の中心へのベクトルです。
軌道伝播モデルを開く
ISSHighPrecisionOrbitPropagationExampleModel.slx を開きます。このモデルには、ルートレベルの出力ポート ブロックに接続された Orbit Propagator ブロックが含まれています。Orbit Propagator ブロックは、例で使用されるすべての摂動加速度を内部的に計算します。ブロックへの入力として、追加の摂動、操作、またはその他の効果を含めることができます。モデルには、ダッシュボードの コールバック ボタンを含む「ミッション分析/視覚化」セクションも含まれています。このボタンをクリックすると、モデルが実行され、Orbit Propagator ブロックで定義された宇宙機を含む新しい satelliteScenario オブジェクトがベース ワークスペースに作成され、衛星シナリオ ビューアー ウィンドウが開きます。このアクションのソース コードを表示するには、コールバック ボタンをダブルクリックします。「ミッション分析/視覚化」セクションは、新しい satelliteScenario オブジェクトを作成するためのスタンドアロン ワークフローであり、この例では使用されません。
mission.mdl = "ISSHighPrecisionOrbitPropagationExampleModel";
open_system(mission.mdl);
Simulink モデルの構成
モデル内の Orbit Propagator ブロックへのパスを定義します。
iss.blk = mission.mdl + "/High Precision Numerical Orbit Propagator";Simulink プロパティ インスペクタで、または set_param を使用してプログラムで宇宙機の初期条件を設定します。
set_param(iss.blk, ... startDate = string(juliandate(mission.StartDate)), ... stateFormatNum = "ICRF state vector", ... inertialPosition = mat2str(iss.X0_icrf), ... inertialVelocity = mat2str(iss.V0_icrf));
上記の 高精度軌道伝播アルゴリズム セクションで概説した摂動加速度を含めるようにプロパゲーターを構成します。まず、中心体の重力プロパティを設定します。
set_param(iss.blk, ... gravityModel = "Spherical harmonics", ... earthSH = "EGM2008", ... useEOPs = "on");
大気抵抗、第三物体の重力、太陽放射圧に関する宇宙機のプロパティを設定します。
set_param(iss.blk, ... useDrag = "on", ... atmosModel = "NRLMSISE-00", ... SpaceWeatherDataFile = "aeroSpaceWeatherData.mat", ... mass = string(iss.Mass), ... dragCoeff = string(iss.DragCoeff), ... dragArea = string(iss.DragArea)); set_param(iss.blk, ... ephemerisModel = "DE405", ... useThirdBodyGravity = "on", ... includeSunGravity = "on", ... includeMoonGravity = "on", ... includeJupiterGravity = "on"); set_param(iss.blk, ... useSRP = "on", ... shadowModel = "Dual cone", ... includeMoonOccultation = "on", ... reflectivityCoeff = string(iss.SRPCoeff), ... srpArea = string(iss.SRPArea));
モデルレベルのソルバー設定を適用し、モデル出力ポート データをタイムテーブル オブジェクトのデータセットとして保存します。
set_param(mission.mdl, ... SolverType = "Variable-step", ... SolverName = "VariableStepAuto", ... RelTol = "1e-12", ... AbsTol = "1e-12", ... StopTime = string(seconds(mission.Duration)), ... SaveOutput = "on", ... OutputSaveName = "yout", ... SaveFormat = "Dataset", ... DatasetSignalFormat = "timetable");
モデルを実行して暦表を収集する
モデルをシミュレートします。Orbit Propagator ブロックは、ICRF 座標フレームで位置と速度の状態を出力するように構成されています。前のセクション (1e-12) でモデルに適用した厳密な許容値設定のため、シミュレーションの実行には数分かかる場合があります。
mission.SimOutput = sim(mission.mdl);
モデル出力データ構造から位置と速度データを抽出します。
iss.EphPosICRF = mission.SimOutput.yout{1}.Values;
iss.EphVelICRF = mission.SimOutput.yout{2}.Values;timetable オブジェクトのミッションから開始データを設定し、時間行を期間から日時に変換します。
iss.EphPosICRF.Properties.StartTime = mission.StartDate; iss.EphPosICRF.Time.TimeZone = "UTC"; iss.EphVelICRF.Properties.StartTime = mission.StartDate; iss.EphVelICRF.Time.TimeZone = "UTC";
エフェメリドを satelliteScenario オブジェクトにインポートする
衛星シナリオ オブジェクトを作成します。この例では、開始時間と終了時間を明示的に指定しないでください。この省略により、衛星シナリオは、satellite() メソッドに渡された timetable データからシナリオの時間範囲を導き出すことができます。
scenario = satelliteScenario;
satellite メソッドを使用して、宇宙機を ICRF 位置および速度 timetable オブジェクトとして satelliteScenario に追加します。
iss.EphPosICRF_m = iss.EphPosICRF; iss.EphPosICRF_m.Data = iss.EphPosICRF.Data*1e3; iss.EphVelICRF_mps = iss.EphVelICRF; iss.EphVelICRF_mps.Data = iss.EphVelICRF.Data*1e3; iss.obj = satellite(scenario, iss.EphPosICRF_m, iss.EphVelICRF_mps, ... CoordinateFrame="inertial", Name="ISS");
軌跡線とのコントラストを高めるために、マーカーの色を暗い色調に更新します。
iss.obj.MarkerColor = "#007F80";
iss.obj.MarkerSize = 10;シナリオの開始時間と終了時間は、timetable オブジェクトの開始時間と終了時間を反映するように自動的に調整されます。
disp("Start: " + string(scenario.StartTime)); disp("Stop: " + string(scenario.StopTime));
Start: 03-Jan-2022 12:00:00 Stop: 04-Jan-2022 12:00:00
衛星シナリオビューアーを開きます。
satelliteScenarioViewer(scenario);
参照軌道をロードし、計算された軌道と比較する
参考文献[1]からISS軌道データを読み込みます。
iss.RefEphemeris = load("ISS_ephemeris.mat", "pos_eme2000", "vel_eme2000");
参照軌道の 4 分間のサンプル レートに合わせてシミュレーション データを再サンプリングします。
iss.EphPosICRF = retime(iss.EphPosICRF, iss.RefEphemeris.pos_eme2000.Time); iss.EphVelICRF = retime(iss.EphVelICRF, iss.RefEphemeris.vel_eme2000.Time);
シミュレーション データと参照軌道間の位置誤差をプロットします。
plot(iss.EphPosICRF.Time, iss.EphPosICRF.Data - iss.RefEphemeris.pos_eme2000.Position); title("ISS High Precision Trajectory Position Error"); xlabel("Time"); ylabel("Position Error (km)"); legend(["\DeltaX_{icrf}","\DeltaY_{icrf}","\DeltaZ_{icrf}"], Location="northwest");
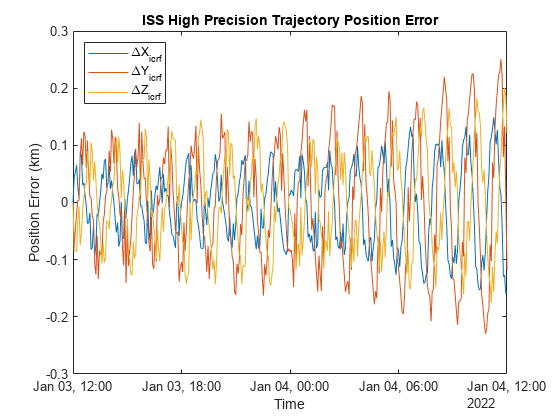
24 時間にわたるシミュレーションと参照データ間の最大誤差は約 0.25 km です。
plot(iss.EphPosICRF.Time, vecnorm(iss.EphPosICRF.Data - iss.RefEphemeris.pos_eme2000.Position, 2, 2)); title("ISS High Precision Trajectory Position Error Magnitude"); xlabel("Time"); ylabel("Position Error (km)");
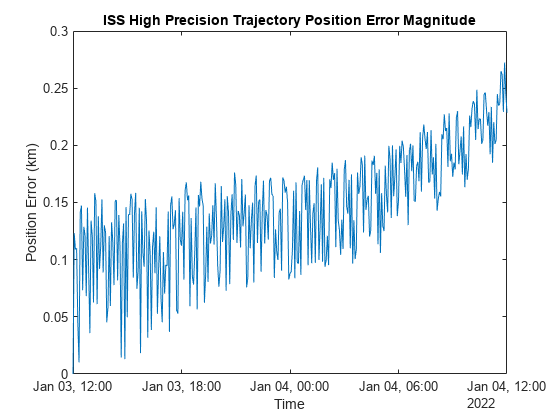
高精度軌道と解析伝播を比較する
比較のために、2 体ケプラー伝播を使用する衛星シナリオに新しい宇宙機を追加します。
初期位置と速度を軌道要素に変換します。
[iss.OrbEl.SemiMajorAxis, ... iss.OrbEl.Eccentricity, ... iss.OrbEl.Inclination, ... iss.OrbEl.RAAN, ... iss.OrbEl.ArgPeriapsis, ... iss.OrbEl.TrueAnomaly] = ijk2keplerian(iss.X0_icrf*1e3, iss.V0_icrf*1e3);
2 体ケプラー伝播を使用して、シナリオに新しい ISS オブジェクトを追加します。
iss.KeplerianOrbit.obj = satellite(scenario, iss.OrbEl.SemiMajorAxis, ... iss.OrbEl.Eccentricity, iss.OrbEl.Inclination, iss.OrbEl.RAAN, ... iss.OrbEl.ArgPeriapsis, iss.OrbEl.TrueAnomaly, ... OrbitPropagator="two-body-keplerian", ... Name="ISS Keplerian"); iss.KeplerianOrbit.obj.Orbit.LineColor = "magenta"; iss.KeplerianOrbit.obj.MarkerColor = "#8E3A59"; iss.KeplerianOrbit.obj.MarkerSize = "10";
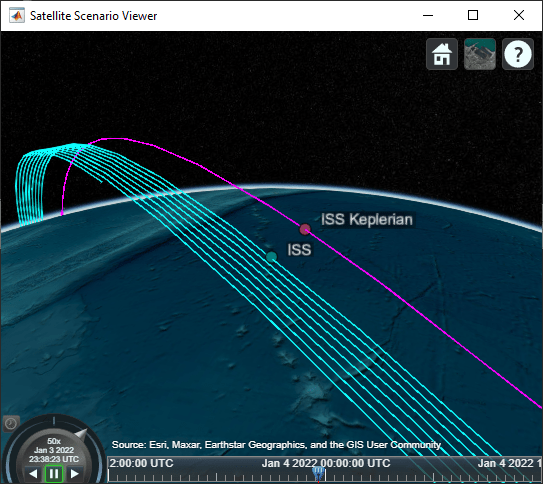
2 体ケプラー伝播の最大誤差をプロットします。
[iss.KeplerianOrbit.EphPosICRFData, ~, ... iss.KeplerianOrbit.TimeSteps] = states(iss.KeplerianOrbit.obj, CoordinateFrame="inertial"); iss.KeplerianOrbit.EphPosICRF = retime(timetable(iss.KeplerianOrbit.TimeSteps', iss.KeplerianOrbit.EphPosICRFData', VariableNames="Data"), ... iss.RefEphemeris.pos_eme2000.Time); plot(iss.EphPosICRF.Time, iss.KeplerianOrbit.EphPosICRF.Data/1e3 - iss.RefEphemeris.pos_eme2000.Position); title("ISS Two Body Keplerian Position Error"); xlabel("Time"); ylabel("Position Error (km)"); legend(["\DeltaX_{icrf}","\DeltaY_{icrf}","\DeltaZ_{icrf}"], Location="northwest");
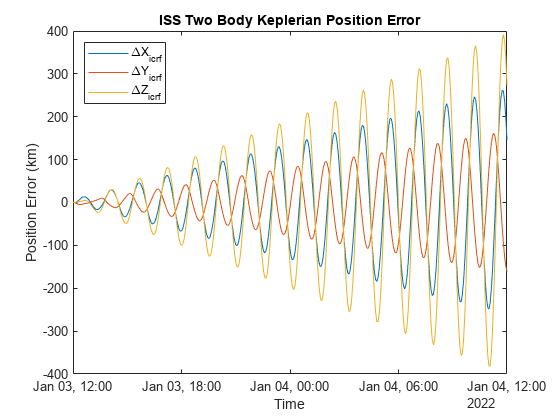
24 時間の接近における二体ケプラー伝播と参照データ間の最大誤差は 450 km を超えますが、高精度数値伝播シミュレーションでは 0.25 km です。
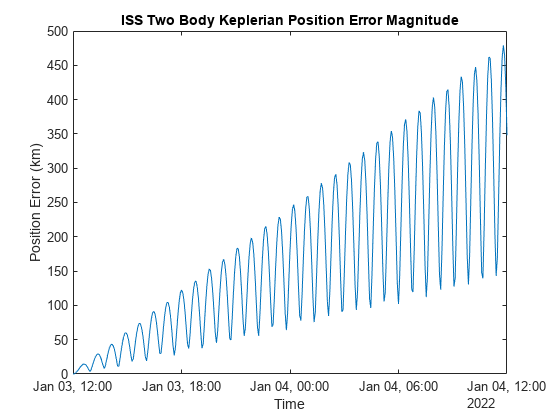
plot(iss.EphPosICRF.Time, vecnorm(iss.KeplerianOrbit.EphPosICRF.Data/1e3 - iss.RefEphemeris.pos_eme2000.Position, 2, 2)); title("ISS Two Body Keplerian Position Error Magnitude"); xlabel("Time"); ylabel("Position Error (km)");
参考文献
[1] NASAオープンデータポータル - 軌道運用および計画(TOPO)、ISS_COORDS_2022-01-03パブリック配布ファイル - https://data.nasa.gov/Space-Science/ISS_COORDS_2022-01-03/ffwr-gv9k
[2] ヴァラド、デイビッド。天体力学の基礎と応用、第 4 版。ホーソーン、カリフォルニア州:マイクロコズムプレス、2013年。