このページは機械翻訳を使用して翻訳されました。最新版の英語を参照するには、ここをクリックします。

航空宇宙座標系について

基本的な座標系の概念

座標系を使用すると、宇宙空間における航空機や宇宙機の位置と方向を追跡できます。Aerospace Blockset™ 座標系は、測地学、天文学、物理学の基本的な概念に基づいています。

定義

ブロックセットは、右手 (RH) 直交座標系を使用します。右手の法則により、座標軸の順序は x-y-z となります。

慣性フレームは、加速しない運動参照フレームです。慣性系では、ニュートンの第 2 法則「力 = 質量 x 加速度」が成り立ちます。大まかに言えば、加速は遠方の宇宙に対して定義され、慣性系は恒星に対しては非加速であるとよく言われます。地球と星は互いに対して非常にゆっくりと動いているので、この仮定は非常に正確な近似値です。

厳密に定義すると、慣性フレームは、互いに対して加速しないすべてのフレームの集合のメンバーです。非慣性フレームとは、慣性フレームに対して加速するフレームのことです。一般に、その加速には並進成分と回転成分の両方が含まれており、その結果、疑似力（疑似重力、およびコリオリの力と遠心力）が発生します。

ブロックセットは、地球の形状 (ジオイド) を、2 つの長い軸 (赤道面 を定義) と、3 つ目のわずかに短い対称軸 (地極) を持つ特殊なタイプの楕円体である扁平回転楕円体としてモデル化します。赤道は赤道面と地球の表面が交差する場所です。地理学的極は、地球の表面と地極軸の交点です。一般的に、地球の地極軸と自転軸は同一ではありません。

緯度は赤道と平行です。経度は地極軸と平行です。経度ゼロまたは本初子午線はイギリスのグリニッジを通過します。

Approximation

ブロックセットは、地球を基準とした座標系を定義する際に 3 つの標準的な近似値を使用します。

• 地球の表面またはジオイドは、長い赤道軸と短い地極軸によって定義される扁平な回転楕円体です。実際には、地球は標準ジオイドに対してわずかに変形しています。

• 地球の自転軸と赤道面は垂直なので、自転軸と地極軸は同一になります。実際には、これらの軸はわずかにずれており、地球が自転すると赤道面が揺れます。この影響はほとんどのアプリケーションでは無視できます。

• 地球固定座標における唯一の非慣性効果は、地球がその軸を中心に回転することによるものです。これは自転する地球中心のシステムです。ブロックセットは、太陽の周りの地球の加速、銀河系内の太陽の加速、宇宙を通る銀河系の加速を無視します。ほとんどのアプリケーションでは、地球の自転のみが重要になります。

  この近似は、地球-月系の外側などの深宇宙に送られる宇宙機では変更する必要があり、太陽中心系が好まれます。

受動的な変換

Aerospace Blockset 内のすべての四元数は受動的な変換です。パッシブ変換では、ベクトルは変更されず、ベクトルが定義されている座標系が回転します。変換の詳細については、「アクティブ変換とパッシブ変換」を参照してください。

他の惑星に対する運動

ブロックセットは標準の WGS-84 ジオイドを使用して地球をモデル化します。赤道軸の長さ、平坦度、回転速度を変更できます。

楕円体のサイズ、平坦度、回転速度を変更することで、楕円体でよく近似される任意の天体に対する宇宙機の動きを表すことができます。天体が西方向（逆行方向）に回転している場合は、回転速度を負にします。

モデリングのための座標系

航空機や宇宙機のモデリングは、機体自体に固定された座標系を使用すると最も簡単になります。航空機の場合、前進方向は風の存在によって変更され、空中での航空機の動きは地面に対する動きと同じではありません。

ブロックセットがボディと風の座標を実装する方法の詳細については、運動方程式 を参照してください。

ボディ座標

非慣性体座標系は、原点と方向の両方が移動中の航空機に対して固定されています。この航空機は剛性があると想定されます。

ボディ座標軸の向きはボディの形状によって固定されます。

• x 軸は機体の先端を通ります。

• y 軸は x 軸の右側 (パイロットの視線方向を向いて) を指し、x 軸に垂直です。

• z 軸は機体の底部を通って下向きに伸び、xy 平面に垂直で、RH ルールを満たしています。

並進自由度

移動は、原点からの距離 x、y、および z でこれらの軸に沿って移動することによって定義されます。

回転自由度

回転はオイラー角 P、Q、R または Φ、Θ、Ψ によって定義されます。これらは次のとおりです。

P または Φ	x軸を中心に回転する
Q または Θ	y軸周りのピッチ
R または Ψ	z軸を中心にヨーイングする

特に指定がない限り、ソフトウェアはデフォルトでオイラー角に ZYX 回転順序を使用します。

風座標

非慣性風座標系の原点は、剛体航空機内に固定されています。座標系の方向は、航空機の速度 V を基準にして定義されます。

風の座標軸の方向は速度 V によって固定されます。

• x 軸は V の方向を指します。

• y 軸は x 軸の右側 (V の方向を向いて) を指し、x 軸に垂直です。

• z 軸は、x 軸と y 軸に関して RH ルールを満たすために必要な方法で xy 平面に垂直を指します。

並進自由度

移動は、原点からの距離 x、y、および z でこれらの軸に沿って移動することによって定義されます。

回転自由度

回転はオイラー角 Φ、γ、χ によって定義されます。

Φ	x軸周りのバンク角
γ	y軸周りの飛行経路
χ	z軸周りの進行方向角度

特に指定がない限り、ソフトウェアはデフォルトでオイラー角に ZYX 回転順序を使用します。

ナビゲーションのための座標系

航空宇宙の軌道をモデル化するには、回転する地球に対して航空機または宇宙機の位置と方向を決定する必要があります。ナビゲーション座標は、地球の中心と表面を基準に定義されます。

地心緯度と測地緯度

地球表面上の 地心緯度 λ は、地球の中心から表面の点までの半径ベクトルと赤道面とのなす角度によって定義されます。

地球表面上の測地緯度 µ は、表面法線ベクトル n と赤道面のなす角度によって定義されます。

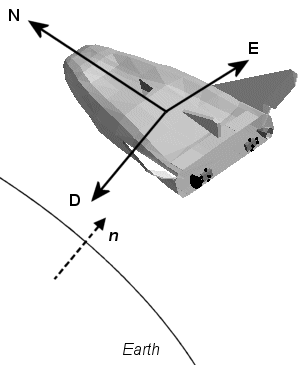
NED 座標

北東下 (NED) システムは、航空機または宇宙機の重心に原点が固定された非慣性システムです。その軸は、地球の表面によって定義された測地方向に沿って配置されています。

• x 軸は、極方向でジオイド面と平行な北を指します。

• y 軸は、緯度曲線に沿って、ジオイド面と平行に東を指します。

• z 軸は地球表面に向かって下向きに向いており、表面の外向きの法線 n と反平行です。

  一定の高度で飛行するということは、地球の表面から一定の z で飛行することを意味します。

ECI 座標

地心慣性（ECI）システムは非回転です。ほとんどのアプリケーションでは、春分点と赤道面は時間の経過とともにわずかに動きますが、このフレームは慣性フレームであると想定します。ECI システムは、赤道と春分点が特定の時代 (例: J2000) で定義されている場合、高精度の軌道計算に対して真に慣性であると見なされます。ECI 座標系の特定の実現を使用する航空宇宙機能およびブロックでは、その情報がドキュメントに提供されています。ECI システムの原点は地球の中心に固定されています (図を参照)。

• x軸は春分点（牡羊座♈の第一点）を指します。

• y 軸は、赤道面内で x 軸の東に 90 度向いています。

• z 軸は地球の自転軸に沿って北を指します。

地球中心座標

ECEF 座標

地球中心、地球固定 (ECEF) システムは非慣性であり、地球とともに回転します。その原点は地球の中心に固定されています (前の図を参照)。

• x ′軸は、地球の赤道面とグリニッジ子午線の交点を指します。

• y ′軸は、赤道面内で x ’軸の東に 90 度向いています。

• z ′軸は地球の自転軸に沿って北を指しています。

表示座標系

Aerospace Blockset 製品では、いくつかの表示ツールを使用できます。それぞれに、モーションをレンダリングするための特定の座標系があります。

MATLAB グラフィック座標

MATLAB^® グラフィックス座標軸の詳細については、座標軸の外観 を参照してください。

MATLAB グラフィックスでは、次のデフォルトの座標軸の方向が使用されます。

• x 軸は画面の外側を指します。

• y 軸は右を指します。

• z軸は上を向いています。

FlightGear 座標

FlightGear は、ブロックセットでサポートされているインターフェースを備えたオープンソースのサードパーティ製フライトシミュレーターです。

• フライトシミュレーターのインターフェースを操作する は FlightGear へのブロックセット インターフェースについて説明します。

• このフライト シミュレーターの詳細については、www.flightgear.org の FlightGear ドキュメントを参照してください。

FlightGear 座標は、標準ボディ座標系から y 軸を中心に -180 度回転した特別なボディ固定システムを形成します。

• x 軸は車両の後方に向かって正になります。

• y 軸は車両の右側に向かって正になります。

• z 軸は上向きが正です。たとえば、ホイールは通常、z 値が最も低くなります。

  

AC3D 座標

AC3D は、https://www.inivis.com から入手できる、低コストで広く使用されているジオメトリ エディターです。ボディ固定座標は、3 つの標準ボディ座標軸を反転することによって形成されます。

• x 軸は車両の後方に向かって正になります。

• y 軸は上向きが正です。たとえば、ホイールは通常、y 値が最も低くなります。

• z 軸は車両の左側が正です。

  

参照

[1] Recommended Practice for Atmospheric and Space Flight Vehicle Coordinate Systems, R-004-1992, ANSI/AIAA, February 1992.

[2] Rogers, R. M., Applied Mathematics in Integrated Navigation Systems, AIAA, Reston, Virginia, 2000.

[3] Sobel, D., Longitude, Walker & Company, New York, 1995.

[4] Stevens, B. L., and F. L. Lewis, Aircraft Control and Simulation, 2nd ed., Aircraft Control and Simulation, Wiley-Interscience, New York, 2003.

[5] Thomson, W. T., Introduction to Space Dynamics, John Wiley & Sons, New York, 1961/Dover Publications, Mineola, New York, 1986.

外部の Web サイト

• 測量局