行列の回転と変換

この例では、Symbolic Math Toolbox™ と行列を使って 3 次元の回転と変換を行う方法を示します。

パラメトリックな表面の定義とプロット

パラメトリックな表面 x(u,v)、y(u,v)、z(u,v) を次のように定義します。

syms u v
x = cos(u)*sin(v);
y = sin(u)*sin(v);
z = cos(v)*sin(v);

fsurf を使用して表面をプロットします。

fsurf(x,y,z)
axis equal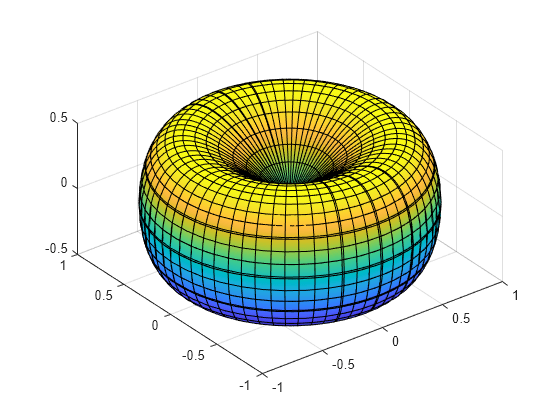

Figure contains an axes object. The axes object contains an object of type parameterizedfunctionsurface.

回転行列の作成

x 軸、y 軸、z 軸を中心とする角度 t の平面回転をそれぞれ表す 3 行 3 列の行列 Rx、Ry および Rz を作成します。

syms t

Rx = [1 0 0; 0 cos(t) -sin(t); 0 sin(t) cos(t)]

Rx = 
 $(\begin{array}{c} 1 & 0 & 0 \\ 0 & \cos (t) & - \sin (t) \\ 0 & \sin (t) & \cos (t) \end{array})$

Ry = [cos(t) 0 sin(t); 0 1 0; -sin(t) 0 cos(t)]

Ry = 
 $(\begin{array}{c} \cos (t) & 0 & \sin (t) \\ 0 & 1 & 0 \\ - \sin (t) & 0 & \cos (t) \end{array})$

Rz = [cos(t) -sin(t) 0; sin(t) cos(t) 0; 0 0 1]

Rz = 
 $(\begin{array}{c} \cos (t) & - \sin (t) & 0 \\ \sin (t) & \cos (t) & 0 \\ 0 & 0 & 1 \end{array})$

各軸を中心とする 3 次元の回転

最初に、表面を x 軸を中心として 45 度反時計回りに回転させます。

xyzRx = Rx*[x;y;z];
Rx45 = subs(xyzRx, t, pi/4);

fsurf(Rx45(1), Rx45(2), Rx45(3))
title('Rotating by \pi/4 about x, counterclockwise')
axis equal

Figure contains an axes object. The axes object with title Rotating by pi / 4 about x, counterclockwise contains an object of type parameterizedfunctionsurface.

z 軸を中心として 90 度時計回りに回転させます。

xyzRz = Rz*Rx45;
Rx45Rz90 = subs(xyzRz, t, -pi/2);

fsurf(Rx45Rz90(1), Rx45Rz90(2), Rx45Rz90(3))
title('Rotating by \pi/2 about z, clockwise')
axis equal

Figure contains an axes object. The axes object with title Rotating by pi / 2 about z, clockwise contains an object of type parameterizedfunctionsurface.

y 軸を中心として 45 度時計回りに回転させます。

xyzRy = Ry*Rx45Rz90;
Rx45Rz90Ry45 = subs(xyzRy, t, -pi/4);

fsurf(Rx45Rz90Ry45(1), Rx45Rz90Ry45(2), Rx45Rz90Ry45(3))
title('Rotating by \pi/4 about y, clockwise')
axis equal

Figure contains an axes object. The axes object with title Rotating by pi / 4 about y, clockwise contains an object of type parameterizedfunctionsurface.

スケーリングと回転

表面を z 軸に沿って係数 3 でスケーリングします。z の式に 3 を乗算して、z = 3*z とすることができます。より一般的な方法は、スケーリング行列を作成した後でスケーリング行列に座標ベクトルを乗算することです。

S = [1 0 0; 0 1 0; 0 0 3];
xyzScaled = S*[x; y; z]

xyzScaled = 
 $(\begin{array}{c} \cos (u) \sin (v) \\ \sin (u) \sin (v) \\ 3 \cos (v) \sin (v) \end{array})$

fsurf(xyzScaled(1), xyzScaled(2), xyzScaled(3))
title('Scaling by 3 along z')
axis equal

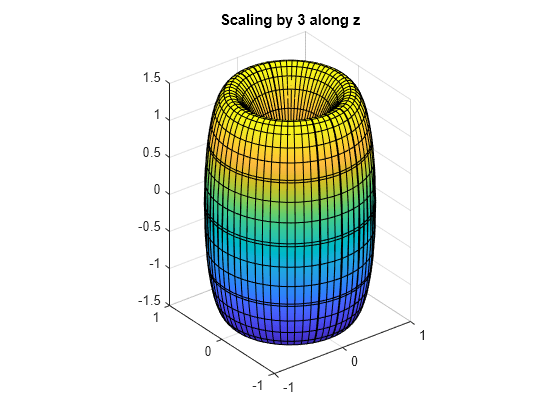
Figure contains an axes object. The axes object with title Scaling by 3 along z contains an object of type parameterizedfunctionsurface.

スケーリングした表面を x 軸、y 軸および z 軸を中心に、z、y、x の順番で 45 度時計回りに回転させます。この変換の回転行列は以下のとおりです。

R = Rx*Ry*Rz

R = 
 $\begin{array}{l} (\begin{array}{c} {\cos (t)}^{2} & - \cos (t) \sin (t) & \sin (t) \\ σ_{1} & {\cos (t)}^{2} - {\sin (t)}^{3} & - \cos (t) \sin (t) \\ {\sin (t)}^{2} - {\cos (t)}^{2} \sin (t) & σ_{1} & {\cos (t)}^{2} \end{array}) \\ where \\ σ_{1} = \cos (t) {\sin (t)}^{2} + \cos (t) \sin (t) \end{array}$

回転行列を使用して新しい座標を求めます。

xyzScaledRotated = R*xyzScaled;
xyzSR45 = subs(xyzScaledRotated, t, -pi/4);

表面をプロットします。

fsurf(xyzSR45(1), xyzSR45(2), xyzSR45(3))
title('Rotating by \pi/4 about x, y, and z, clockwise')
axis equal

Figure contains an axes object. The axes object with title Rotating by pi / 4 about x, y, and z, clockwise contains an object of type parameterizedfunctionsurface.

回転行列 `R` の特性の確認

回転行列は直交行列です。したがって、R の転置はその逆でもあり、R の行列式は 1 です。

simplify(R.'*R)

ans = 
 $(\begin{array}{c} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array})$

simplify(det(R))

ans =  $1$