ライブ エディターにおけるシンボリック ワークフローの次のステップの提案

単純化 (シンボリック式)

指数関数と虚数を含むシンボリック式を作成します。以下のコードを実行して、シンボリック出力を生成します。

syms x
expr = 1i*(exp(-1i*x) - exp(1i*x))/(exp(-1i*x) + exp(1i*x))

expr = 
$$\frac{{\mathrm{e}}^{-x\hspace{0.17em}\mathrm{i}}\hspace{0.17em}\mathrm{i}-{\mathrm{e}}^{x\hspace{0.17em}\mathrm{i}}\hspace{0.17em}\mathrm{i}}{{\mathrm{e}}^{-x\hspace{0.17em}\mathrm{i}}+{\mathrm{e}}^{x\hspace{0.17em}\mathrm{i}}}$$

式を単純化するには、シンボリック出力を右クリックして [式の書き換えと単純化]、[式の単純化] を選択します。

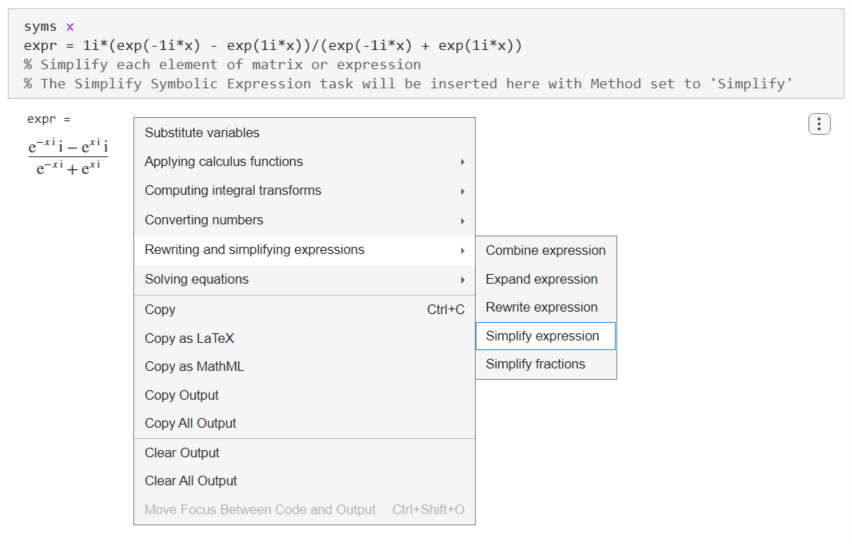
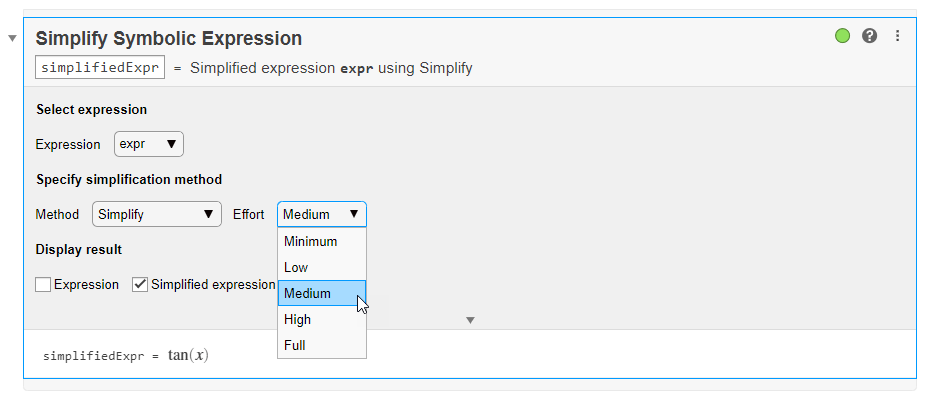
ライブ エディターによって [単純化 (シンボリック式)] ライブ タスクが挿入および適用され、対話形式でシンボリック式の単純化や再配置を行います。より単純な結果を得るには、計算エフォートを [中] に変更します。

係数の代入と 2 次方程式の求解

係数 $$a$$、$$b$$、$$c$$ を持つ 2 次方程式を作成します。以下のコードを実行して、シンボリック出力を生成します。

syms a b c x
eqn = a*x^2 + b*x + c == 0

eqn = $$a\hspace{0.17em}{x}^2+b\hspace{0.17em}x+c=0$$

式の中の係数に代入するには、出力を右クリックして [変数の置換] を選択します。

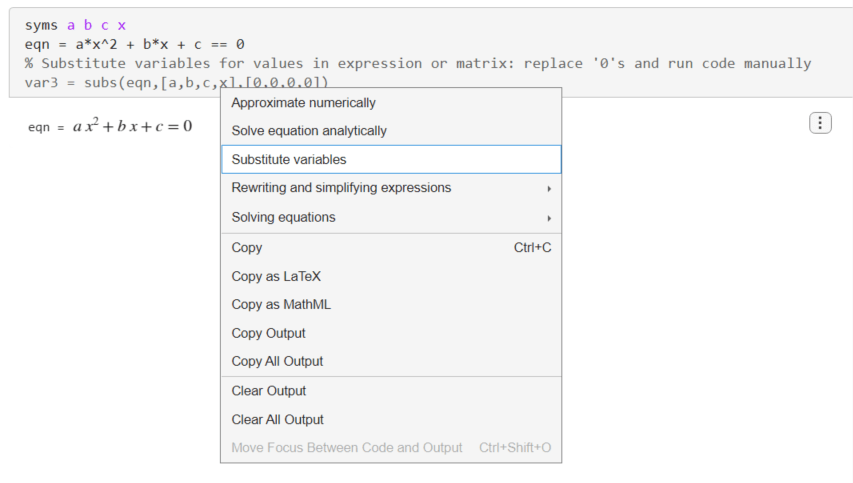
ライブ エディターによって、式の中の係数や変数に代入する関数 subs が挿入されます。関数 subs について、ライブ エディターが自動的に関数を実行することはありません。$$a=3$$、$$b=2$$、$$c=0$$ に置換するには、関数 subs の 2 番目および 3 番目の引数を [a,b,c] および [3,2,0] に変更します。その後、ライブ エディターのセクションを実行して、関数 subs を適用します。

var3 = subs(eqn,[a,b,c],[3,2,0])

var3 = $$3\hspace{0.17em}{x}^2+2\hspace{0.17em}x=0$$

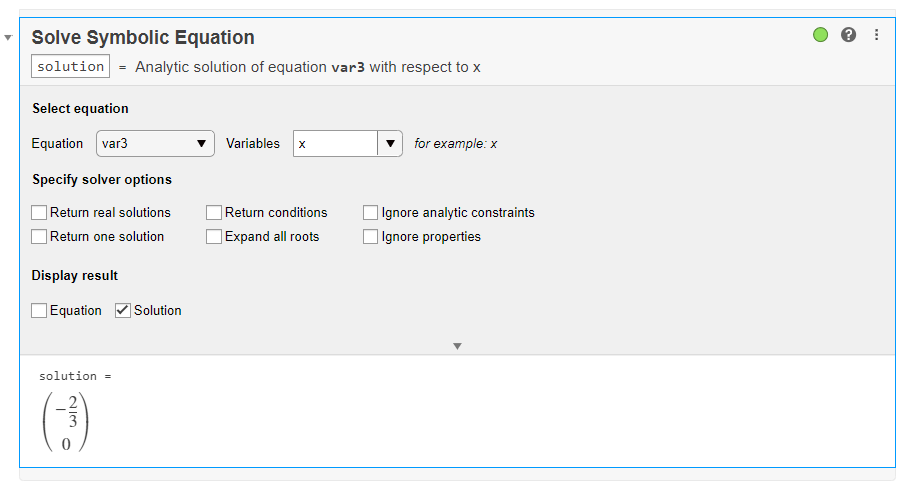
この 2 次方程式を解くには、出力を右クリックして [方程式を解析的に求解] を選択します。

ライブ エディターによって、[求解 (シンボリック式)] ライブ タスクが挿入および適用され、対話形式でシンボリック方程式の解析解を求めます。

陽関数および陰関数のプロット

3 つのシンボリック変数 x、y、z と 1 つの正弦波関数を作成します。以下のコードを実行して、シンボリック出力を生成します。

syms x y z
f = sin(2*x)

f = $$\sin \left(2\hspace{0.17em}x\right)$$

正弦波の関数をプロットするには、出力を右クリックして [関数をプロット]、[関数のプロット] を選択します。

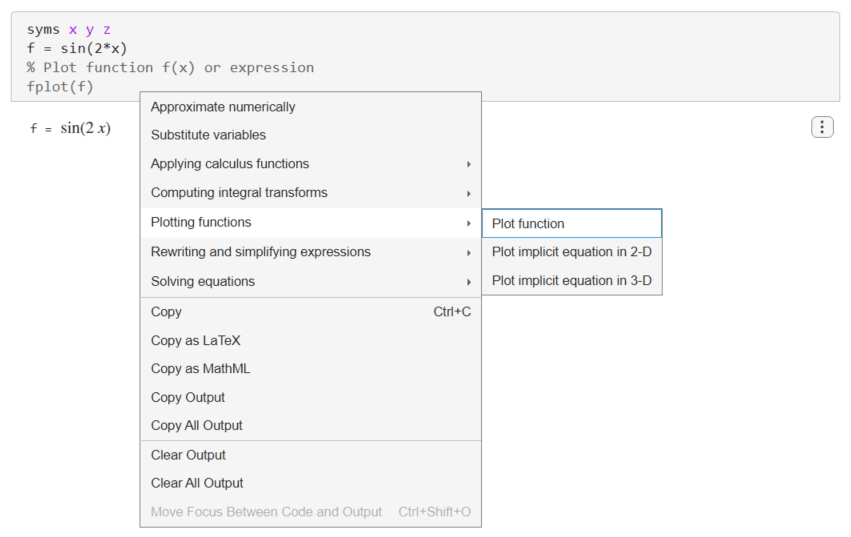
ライブ エディターによって、fplot を使用して正弦波関数がプロットされます。

fplot(f)

次に、双曲線を表す方程式を作成します。以下のコードを実行して、シンボリック出力を生成します。

eqn = x^2 - y^2 == 1

eqn = $$x^2-y^2=1$$

正弦波関数をプロットするには、出力を右クリックして、[関数をプロット]、[陰的な方程式を 2-D でプロット] を選択します。

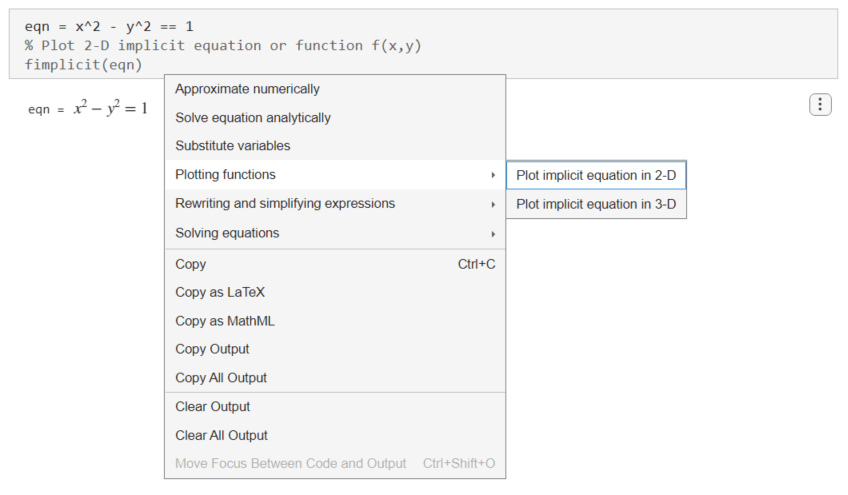
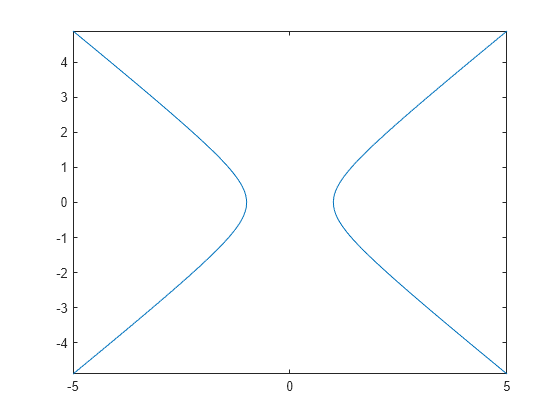
ライブ エディターによって、fimplicit を使用して双曲線がプロットされます。

fimplicit(eqn)

次に、トーラスを表すシンボリック関数を作成します。以下のコードを実行して、シンボリック出力を生成します。

f(x,y,z) = (x^2 + y^2 + z^2 + 3^2 - 2^2)^2 - 4*3^2*(x^2+y^2)

f(x, y, z) = $${\left(x^2+y^2+z^2+5\right)}^2-36\hspace{0.17em}{x}^2-36\hspace{0.17em}{y}^2$$

トーラスをプロットするには、出力を右クリックして [陰的な方程式を 3-D でプロット] を選択します。

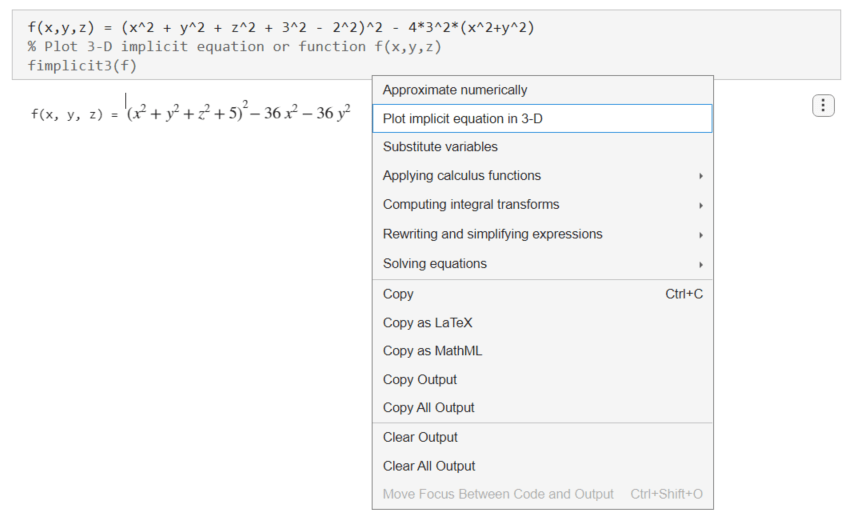
ライブ エディターによって、fimplicit3 を使用してトーラスがプロットされます。

fimplicit3(f)

行列関数の適用

3 つのシンボリック変数 x、y、z と 1 つのシンボリック行列を作成します。以下のコードを実行して、シンボリック出力を生成します。

syms x y z
M1 = sym([x^2 + a, x; y + 2, 3*y^2])

M1 = 
$$\left(\begin{array}{cc}{x}^2+a& x\\ y+2& 3\hspace{0.17em}{y}^2\end{array}\right)$$

行列の逆行列を求めるには、出力を右クリックして [行列関数を適用]、[逆行列を計算] を選択します。[行列関数を適用]、[逆行列を計算] という提案は、シンボリック出力がシンボリック行列の場合にのみ利用可能です。

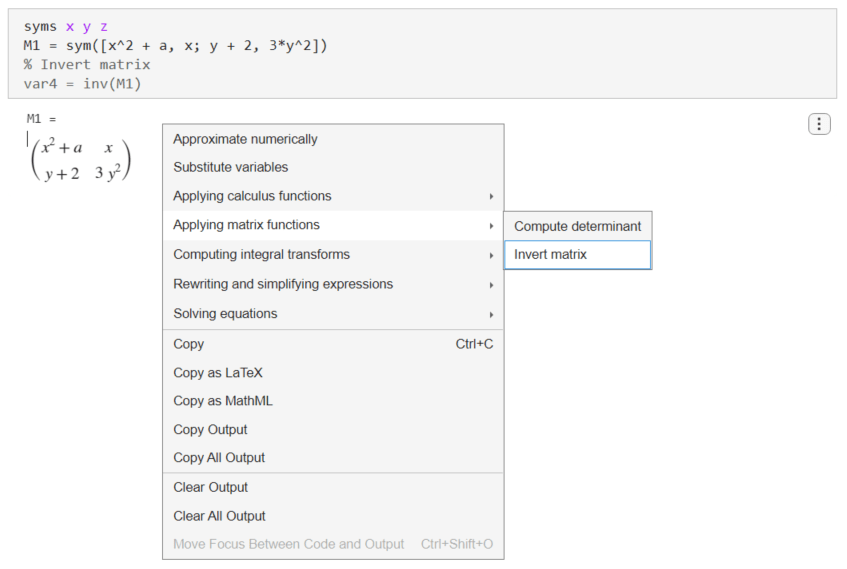
ライブ エディターによって関数 inv が挿入および適用され、行列の逆行列が得られます。

var4 = inv(M1)

var4 = 
$$\begin{array}{l}\left(\begin{array}{cc}-\frac{3\hspace{0.17em}{y}^2}{{\sigma }_1}& \frac{x}{{\sigma }_1}\\ \frac{y+2}{{\sigma }_1}& -\frac{x^2+a}{{\sigma }_1}\end{array}\right)\\ \\ \mathrm{where}\\ \\ \mathrm{ }{\sigma }_1=-3\hspace{0.17em}{x}^2\hspace{0.17em}{y}^2+x\hspace{0.17em}y+2\hspace{0.17em}x-3\hspace{0.17em}a\hspace{0.17em}{y}^2\end{array}$$

次に、1 行 3 列のシンボリック ベクトルを作成します。以下のコードを実行して、シンボリック出力を生成します。

M2 = sym([x*y*z, y^2, x + z])

M2 = $$\left(\begin{array}{ccc}x\hspace{0.17em}y\hspace{0.17em}z& y^2& x+z\end{array}\right)$$

ベクトルのヤコビアンを計算するには、出力を右クリックして [行列関数を適用]、[ベクトルのヤコビ行列の計算] を選択します。[行列関数を適用]、[ベクトルのヤコビ行列の計算] という提案は、シンボリック出力がシンボリック ベクトルである場合にのみ利用可能です。

ライブ エディターによって関数 jacobian が挿入および適用され、ベクトルのヤコビアンが計算されます。

var5 = jacobian(M2)

var5 = 
$$\left(\begin{array}{ccc}y\hspace{0.17em}z& x\hspace{0.17em}z& x\hspace{0.17em}y\\ 0& 2\hspace{0.17em}y& 0\\ 1& 0& 1\end{array}\right)$$

次に、1 行 3 列の別のシンボリック ベクトルを作成します。以下のコードを実行して、シンボリック出力を生成します。

M3 = sym([x^2*y, 2*x, z])

M3 = $$\left(\begin{array}{ccc}{x}^2\hspace{0.17em}y& 2\hspace{0.17em}x& z\end{array}\right)$$

ベクトルの回転を計算するには、出力を右クリックして [行列関数を適用]、[ベクトル場の回転を計算] を選択します。

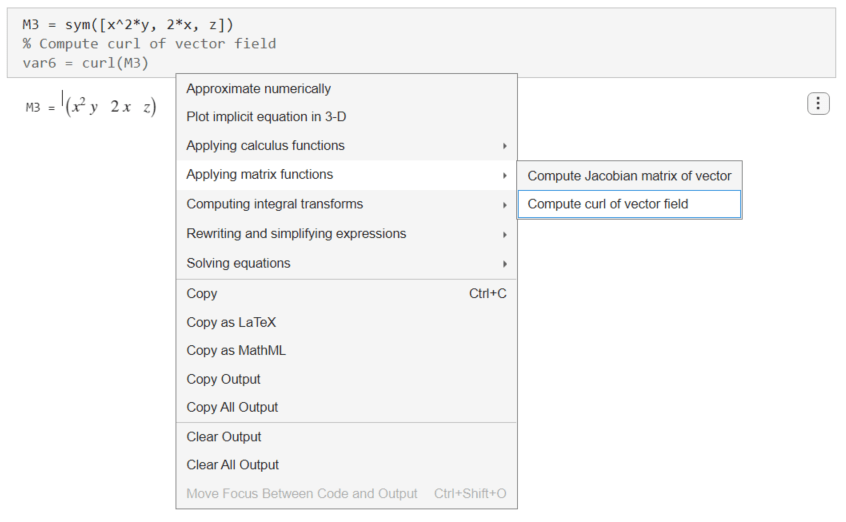
ライブ エディターによって関数 curl が挿入および適用され、ベクトルの回転が計算されます。

var6 = curl(M3)

var6 = 
$$\left(\begin{array}{c}0\\ 0\\ 2-x^2\end{array}\right)$$

微分方程式の求解、積分変換の計算、極の求解

2 階微分方程式を作成します。以下のコードを実行して、シンボリック出力を生成します。

syms f(x) s
eqn = diff(f,x,x) == -9*f

eqn(x) = 
$$\frac{{\partial }^2}{\partial x^2}\mathrm{ }f\left(x\right)=-9\hspace{0.17em}f\left(x\right)$$

この微分方程式を解くには、出力を右クリックして [微分方程式を解く] を選択します。[微分方程式を解く] という提案は、シンボリック出力が微分方程式である場合にのみ利用可能です。

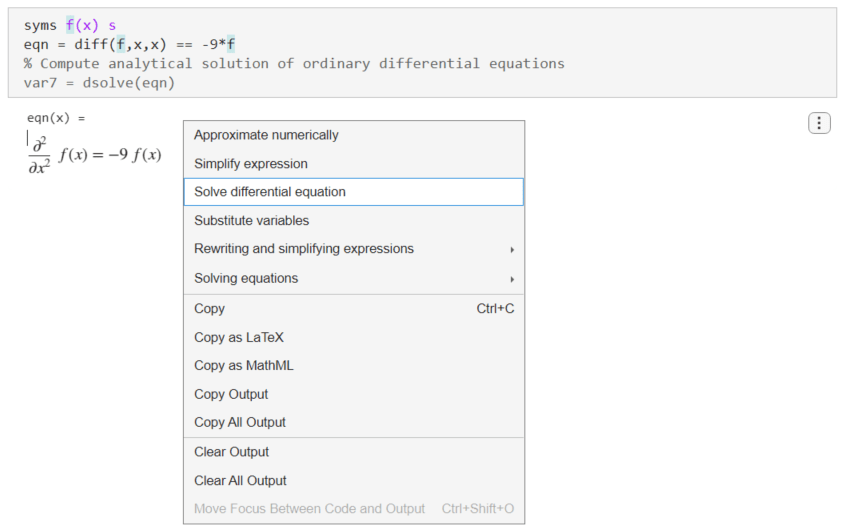
ライブ エディターによって関数 dsolve が挿入および適用され、微分方程式が解かれます。

var7 = dsolve(eqn)

var7 = $$C_1\hspace{0.17em}\cos \left(3\hspace{0.17em}x\right)-C_2\hspace{0.17em}\sin \left(3\hspace{0.17em}x\right)$$

次に、解のラプラス変換を求めます。dsolve の出力を右クリックし、[積分変換を計算]、[ラプラス変換を計算] を選択します。

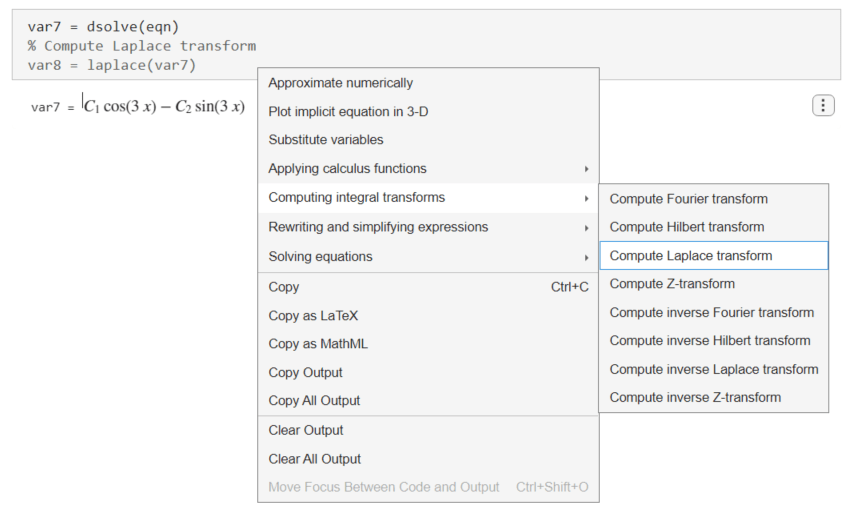
ライブ エディターによって関数 laplace が挿入および適用され、ラプラス変換が計算されます。

var8 = laplace(var7)

var8 = 
$$\frac{C_1\hspace{0.17em}s}{s^2+9}-\frac{3\hspace{0.17em}{C}_2}{s^2+9}$$

最後に、ラプラス変換の極を求めます。ラプラス変換の出力を右クリックし、[微積分関数を適用]、[関数の極の計算] を選択します。

ライブ エディターによって関数 poles が挿入および適用され、極が計算されます。

var9 = poles(var8,s)

var9 = 
$$\left(\begin{array}{c}-3\hspace{0.17em}\mathrm{i}\\ 3\hspace{0.17em}\mathrm{i}\end{array}\right)$$

単位の変換および単位の整合性のチェック

単位が異なる 2 つの長さの比を作成します。以下のコードを実行して、シンボリック出力を生成します。

u = symunit;
ratio = (7*u.mi)/(420*u.ft)

ratio = 
$$\frac{1}{60}\hspace{0.17em}\frac{\mathrm{mi}\mathrm{"mile\; -\; a\; physical\; unit\; of\; length."}}{\mathrm{ft}\mathrm{"foot\; -\; a\; physical\; unit\; of\; length."}}$$

単位をメートル、グラム、秒の単位系に変換します。出力を右クリックし、[物理単位関数を適用]、[単位を変換] を選択します。[物理単位関数を適用] という提案は、シンボリック出力にシンボリック単位が含まれている場合にのみ利用可能です。

ライブ エディターによって関数 unitConvert が挿入および適用され、単位がメートル、グラム、秒の単位系に変換されます。

var10 = unitConvert(ratio,[symunit('m'),symunit('g'),symunit('s')])

var10 = $$88$$

次に、移動発射体の $$x$$ 座標と $$y$$ 座標を表す 2 つのシンボリック式 x と y を作成します。x と y の単位と長さの単位 m および ft を比較するシンボリック式 r を作成します。以下のコードを実行して、シンボリック出力を生成します。

syms theta ts x y r
g = 9.81*u.m/u.s^2;
v = 10*u.m/u.s;
t = ts*u.s;
x = v*cos(theta)*t;
y = v*sin(theta)*t + (-g*t^2)/2;
r = [x == u.m y == u.ft]

r = 
$$\left(\begin{array}{cc}10\hspace{0.17em}\mathrm{ts}\hspace{0.17em}\cos \left(\theta \right)\hspace{0.17em}\mathrm{m}\mathrm{"meter\; -\; a\; physical\; unit\; of\; length."}=\mathrm{m}\mathrm{"meter\; -\; a\; physical\; unit\; of\; length."}& 10\hspace{0.17em}\mathrm{ts}\hspace{0.17em}\sin \left(\theta \right)\hspace{0.17em}\mathrm{m}\mathrm{"meter\; -\; a\; physical\; unit\; of\; length."}-\frac{981\hspace{0.17em}{\mathrm{ts}}^2}{200}\hspace{0.17em}\mathrm{m}\mathrm{"meter\; -\; a\; physical\; unit\; of\; length."}=\mathrm{ft}\mathrm{"foot\; -\; a\; physical\; unit\; of\; length."}\end{array}\right)$$

r の単位の整合性をチェックします。出力を右クリックし、[物理単位関数を適用]、[単位の整合性をチェック] を選択します。

ライブ エディターによって関数 checkUnits が挿入および適用され、r の単位の一貫性と互換性がチェックされます。

関数 checkUnits は、フィールド Consistent とフィールド Compatible を含む構造体を返します。Consistent フィールドは、r のすべての項が同じ次元、同じ単位で、換算係数が 1 の場合、logical 1(true) を返します。Compatible フィールドは、すべての項が同じ次元を持っている場合、logical 1(true) を返しますが、同じ単位である必要はありません。

var11 = checkUnits(r)

var11 = struct with fields:
    Consistent: [1 0]
    Compatible: [1 1]