ヒルベルト行列と逆行列
この例では、Symbolic Math Toolbox™ を使ってヒルベルト行列の逆行列を計算する方法を説明します。
定義 :ヒルベルト行列は要素が単位分数になる正方行列です。たとえば、3x3 のヒルベルト行列は、 となります。
純粋な数値法では失敗する悪条件の行列の場合でも、シンボリック計算では正確な結果が得られます。
20 行 20 列の数値ヒルベルト行列を作成します。
H = hilb(20);
この行列の条件数を求めます。ヒルベルト行列は悪条件の行列です。つまり、大きな条件数をもち、こういった行列がほぼ特異であることを示しています。条件数の計算でも数値誤差が発生しやすいことに注意してください。
cond(H)
ans = 2.1065e+18
したがって、ヒルベルト行列の逆行列は数値的に不安定です。逆行列を計算する場合、H*inv(H) は単位行列または許容誤差範囲内の単位行列に近い行列を返さなければなりません。
はじめに、関数 inv を使用して H の逆行列を計算します。数値的に不安定なため警告がスローされます。
H*inv(H)
Warning: Matrix is close to singular or badly scaled. Results may be inaccurate. RCOND = 9.542396e-20.
ans = 20×20
1.0000 -0.0000 -0.0003 0.0044 0.0212 -0.2436 0.4383 -0.6683 -0.4409 0.6464 -0.9986 -0.4477 8.3067 -0.2302 -0.4680 -0.4770 1.4327 -1.4875 8.0000 2.0000
0.4314 1.0000 -0.0002 0.0003 0.0528 -0.0284 0.9397 0.6603 -0.1158 1.3085 -0.5132 0.2835 0.5888 -1.7213 0.7195 -1.7957 0.6355 2.8214 -8.0000 2.0000
0.7987 -0.8048 0.9997 -0.0041 0.1027 0.1222 0.5629 -0.1333 0.5837 1.0126 -0.9596 0.1601 -0.3606 -2.5592 0.5373 -2.9668 -0.2067 3.8693 -8.0000 0
1.0486 -1.6648 0.4041 0.9885 0.0958 -0.1427 1.3149 0.2797 -0.1724 0.8018 -0.1066 0.3468 5.6058 -2.5304 2.5296 -3.6839 -0.4191 3.5598 -16.0000 1.0000
1.2164 -2.4406 1.0946 -0.1853 1.1204 -0.1147 1.2598 -0.9847 0.2424 -0.0230 0.5197 0.8731 3.8277 -4.7249 0.5983 -2.3525 -0.3189 3.4062 -4.0000 3.0000
1.3286 -3.1054 1.9447 -0.5911 0.1962 0.8550 1.2190 -1.0755 0.2927 1.1158 0.2254 0.9657 3.0420 -2.0190 1.2346 -1.7681 -0.4577 3.5038 0 0
1.4027 -3.6617 2.8529 -1.1814 0.3594 -0.2091 2.4910 -0.4949 0.6416 0.4732 0.2943 -0.5944 4.9283 -4.1578 1.6593 -3.0688 -0.1768 4.6058 0 2.0000
1.4501 -4.1206 3.7522 -1.8860 0.5367 0.0995 0.2101 1.4302 -1.0067 1.5837 -1.5936 3.3039 -0.4865 0.0223 0.9902 -1.7856 -0.3147 2.2500 0 0
1.4784 -4.4954 4.6045 -2.6478 0.8130 0.1115 0.0798 0.1202 1.1006 0.0361 -0.2599 3.4626 -0.4334 -0.7285 -0.3979 0.2157 0.6016 0.2411 0 -1.0000
1.4930 -4.7986 5.3893 -3.4322 1.1685 -0.0259 0.4050 -0.0399 1.2269 0.7081 0.0601 0.9479 3.7747 -2.1672 1.9212 -1.5514 0.2045 2.7134 -4.0000 0
1.4975 -5.0417 6.0972 -4.1834 1.4561 0.0771 0.5520 0.5281 -0.6765 -0.0921 0.7289 3.0746 -0.6345 0.4550 -0.3803 0.3295 0.9800 -1.4188 0 -2.0000
1.4946 -5.2346 6.7274 -4.9048 1.7749 -0.0877 0.2437 0.2317 -0.2408 0.4926 -0.4823 1.3380 0.1269 -0.8290 1.0542 -1.0679 0.4138 0.2460 4.0000 0
1.4863 -5.3854 7.2827 -5.5776 2.1172 -0.0469 0.6250 -0.6250 0.3750 0.4062 0.1250 -0.2500 3.5000 -2.5000 1.1250 -0.5000 -0.5312 2.7500 8.0000 0
1.4740 -5.5013 7.7675 -6.1883 2.4591 -0.2935 1.0419 -0.5056 0.8891 0.4459 0.1519 -2.2266 4.4263 -3.3728 2.6915 -2.1445 -0.8045 3.5795 0 0
1.4587 -5.5879 8.1875 -6.7353 2.6649 0.0763 -0.5718 0.7748 -0.3322 -0.2596 0.1983 1.3305 -3.3098 -0.4367 -0.3577 1.1951 0.2617 -0.9577 0 0
⋮
ここで、ヒルベルト行列の精度を高める MATLAB® 関数 invhilb を使用します。この関数は 15 行 15 列までの厳密なヒルベルト行列の逆行列を見つけます。20 行 20 列のヒルベルト行列の場合、invhilb は逆行列の近似を求めます。
H*invhilb(20)
ans = 20×20
1010 ×
0.0000 -0.0000 0.0000 -0.0000 0.0000 -0.0004 0.0013 -0.0037 0.0047 -0.2308 0.4019 0.2620 -0.4443 -7.5099 3.4753 3.2884 -1.1618 0.2301 0.4295 0.0537
-0.0000 0.0000 -0.0000 0.0000 -0.0000 -0.0001 -0.0009 0.0172 -0.0628 0.1251 -0.8975 2.7711 -2.8924 -1.4888 -2.5102 6.4897 -3.0581 0.7925 0 -0.0268
0.0000 0.0000 0.0000 -0.0000 -0.0000 -0.0001 0.0009 0.0042 -0.0303 0.0271 -0.1028 0.2862 -0.9267 -4.0597 1.8194 4.7727 -1.3255 0.4667 0.2147 -0.0268
0.0000 0.0000 -0.0000 -0.0000 0.0000 -0.0001 0.0004 0.0002 -0.0056 0.0526 -0.1136 0.3616 -1.6920 -3.7214 0.2709 4.4169 -1.1602 0.5541 0 -0.0268
-0.0000 0.0000 -0.0000 0.0000 -0.0000 -0.0000 -0.0006 0.0068 -0.0394 0.1449 -0.7818 1.9314 -2.1273 -1.0745 -2.2988 4.6349 -1.8923 0.3793 0.2147 0.0537
0.0000 -0.0000 0.0000 -0.0000 0.0000 -0.0002 0.0014 -0.0028 0.0304 -0.1053 -0.0724 -0.2073 -0.3769 -5.0729 2.7552 2.3488 -0.5046 0.2240 0 0
-0.0000 0.0000 -0.0000 0.0000 -0.0000 0.0000 -0.0013 0.0101 -0.0520 0.1307 -0.7715 2.9297 -3.3374 1.4084 -3.8703 7.1053 -2.7578 0.8815 -0.2147 0
0.0000 -0.0000 0.0000 -0.0000 -0.0000 -0.0002 0.0018 -0.0040 0.0231 -0.0892 0.2000 0.2766 -0.8262 -4.7229 1.6513 2.1857 -0.4749 -0.1747 0 0
-0.0000 0.0000 -0.0000 0.0000 -0.0000 0.0000 0.0004 0.0144 -0.0513 0.1165 -0.7063 1.9776 -2.0602 -1.0763 -3.2081 3.8539 -2.4580 0.5675 0 0.0268
0.0000 0.0000 0.0000 -0.0000 0.0000 -0.0002 0.0008 -0.0019 0.0027 -0.0167 -0.0497 0.8865 -0.6720 -1.2729 0.0571 2.3625 -1.2616 0.2443 0.2147 0
-0.0000 0.0000 -0.0000 0.0000 -0.0000 -0.0001 0.0004 0.0050 -0.0400 0.0368 -0.4875 1.2090 -1.1395 -0.8712 -0.3376 3.4449 -1.6401 0.3319 -0.2147 0.0268
0.0000 0.0000 0.0000 -0.0000 0.0000 -0.0001 0.0009 -0.0015 -0.0172 0.0267 -0.1909 0.1515 -0.2069 -2.4186 -0.1889 3.6202 -0.9900 0.3459 -0.2147 -0.0268
-0.0000 0.0000 -0.0000 0.0000 -0.0000 -0.0000 0.0007 0.0097 -0.0384 0.0201 -0.3053 1.3925 -2.2012 -1.1811 -0.7248 3.8588 -1.6106 0.5679 -0.2147 0
0.0000 -0.0000 -0.0000 -0.0000 -0.0000 -0.0001 0.0007 0.0020 -0.0014 -0.0255 -0.1178 0.7277 -0.7834 -2.9257 1.2532 2.2557 -0.7382 0.3044 0 -0.0134
-0.0000 0.0000 -0.0000 -0.0000 -0.0000 -0.0001 0.0000 0.0043 -0.0304 0.0353 -0.3375 0.7563 -1.3325 -2.0856 -1.4510 3.1561 -1.1128 0.4057 0.2147 0
⋮
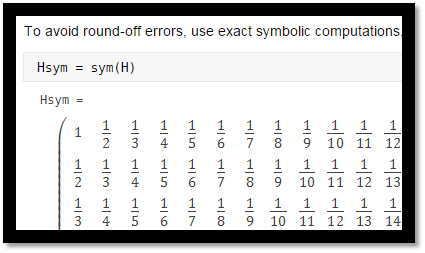
丸め誤差を回避するために、厳密なシンボリック計算を使用します。ここでは、シンボリック ヒルベルト行列を作成します。
Hsym = sym(H)
Hsym =
条件数の値を取得します。シンボリック メソッドから導出されたので数値誤差がありません。
vpa(cond(Hsym))
ans =
条件数が大きくても厳密な逆行列を計算できます。
Hsym*inv(Hsym)
ans =