`tsne` の設定

この例では、さまざまな tsne の設定の影響を示します。

データの取得

はじめに、MNIST [1] のイメージとラベルのデータを以下から取得します。

https://yann.lecun.com/exdb/mnist/

ファイルを解凍します。この例では t10k-images データを使用します。

imageFileName = 't10k-images.idx3-ubyte';
labelFileName = 't10k-labels.idx1-ubyte';

ファイルを処理してワークスペースに読み込みます。この処理関数のコードは、この例の終わりで示します。

[X,L] = processMNISTdata(imageFileName,labelFileName);

Read MNIST image data...
Number of images in the dataset:  10000 ...
Each image is of 28 by 28 pixels...
The image data is read to a matrix of dimensions:  10000 by  784...
End of reading image data.

Read MNIST label data...
Number of labels in the dataset:  10000 ...
The label data is read to a matrix of dimensions:  10000 by  1...
End of reading label data.

t-SNE の使用によるデータの処理

t-SNE を使用して、データクラスターの 2 次元類似物を取得します。この大規模なデータセットでパフォーマンスを向上させるため、Barnes-Hut アルゴリズムを使用します。PCA を使用して、初期次元を 784 から 50 に削減します。

rng default % for reproducibility
Y = tsne(X,'Algorithm','barneshut','NumPCAComponents',50);
figure
numGroups = length(unique(L));
clr = hsv(numGroups);
gscatter(Y(:,1),Y(:,2),L,clr)
title('Default Figure')

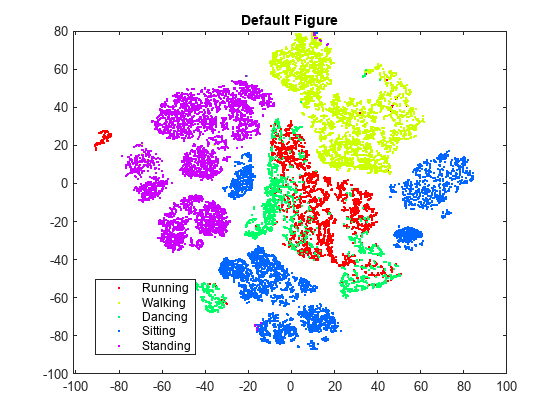
t-SNE は、クラスターが十分に分離されており、位置が正しくないと思われるデータ点の個数が比較的少ない図を作成します。

パープレキシティ

パープレキシティの設定を変更して、図に対する影響を調べます。

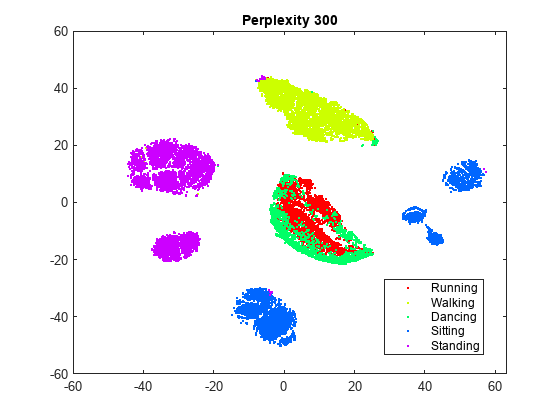
rng default % for fair comparison
Y100 = tsne(X,'Algorithm','barneshut','NumPCAComponents',50,'Perplexity',100);
figure
gscatter(Y100(:,1),Y100(:,2),L,clr)
title('Perplexity 100')

rng default % for fair comparison
Y4 = tsne(X,'Algorithm','barneshut','NumPCAComponents',50,'Perplexity',4);
figure
gscatter(Y4(:,1),Y4(:,2),L,clr)
title('Perplexity 4')

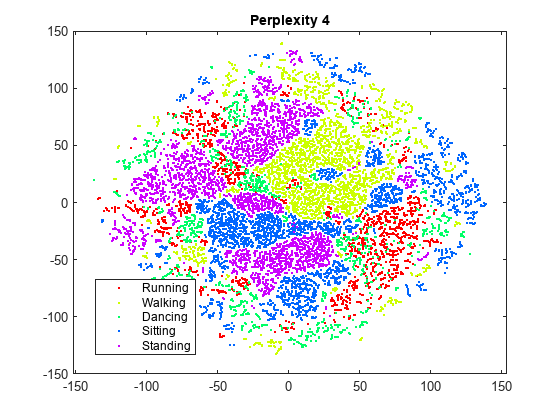
パープレキシティを 100 に設定すると、大部分が既定の図に似ている図が生成されます。クラスターは既定の設定の場合より緊密です。しかし、パープレキシティを 4 に設定すると、クラスターが十分には分離されない図が生成されます。クラスターは既定の設定の場合よりばらばらです。

強調

強調の設定を変更して、図に対する影響を調べます。

rng default % for fair comparison
YEX0 = tsne(X,'Algorithm','barneshut','NumPCAComponents',50,'Exaggeration',20);
figure
gscatter(YEX0(:,1),YEX0(:,2),L,clr)
title('Exaggeration 20')

rng default % for fair comparison
YEx15 = tsne(X,'Algorithm','barneshut','NumPCAComponents',50,'Exaggeration',1.5);
figure
gscatter(YEx15(:,1),YEx15(:,2),L,clr)
title('Exaggeration 1.5')

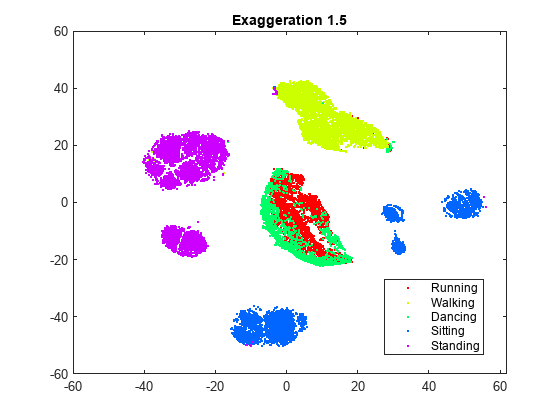
強調の設定は図に影響を与えますが、既定ではない設定にすると既定の設定より良好な図が得られるかどうかは明らかではありません。強調が 20 の図は既定の図と似ています。一般に、強調が大きくなると、埋め込まれるクラスターの間に作成される空白の空間が多くなります。強調が 1.5 になると、1 および 6 というラベルのグループがそれぞれ 2 つのグループに分割され、望ましくない結果になります。X の同時分布の値を強調すると、Y の同時分布の値が小さくなります。これにより、埋め込まれる点が互いに対してはるかに移動しやすくなります。クラスター 1 および 6 の分割は、この効果を反映しています。

学習率

学習率の設定を変更して、図に対する影響を調べます。

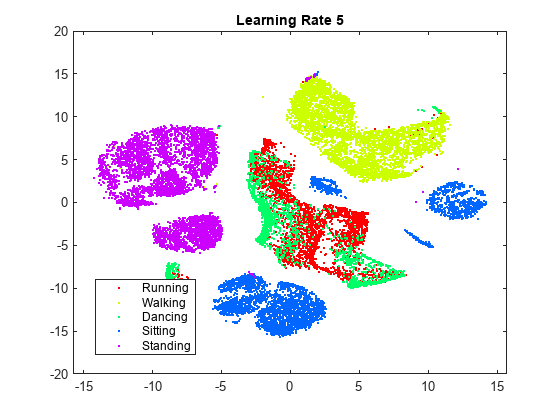
rng default % for fair comparison
YL5 = tsne(X,'Algorithm','barneshut','NumPCAComponents',50,'LearnRate',5);
figure
gscatter(YL5(:,1),YL5(:,2),L,clr)
title('Learning Rate 5')

rng default % for fair comparison
YL2000 = tsne(X,'Algorithm','barneshut','NumPCAComponents',50,'LearnRate',2000);
figure
gscatter(YL2000(:,1),YL2000(:,2),L,clr)
title('Learning Rate 2000')

学習率が 5 の図では、いくつかのクラスターが 2 つ以上に分割されています。これは、学習率が小さすぎると、不適切な局所的最小値で最小化処理が止まる可能性があることを示しています。学習率が 2000 になると、既定の図と似た図になります。

さまざまな設定での初期動作

学習率または強調値が大きいと、望ましくない初期動作になる可能性があります。これを調べるため、これらのパラメーターに大きい値を設定し、すべての反復を表示するため NumPrint と Verbose を 1 に設定します。この実験の目標は初期動作を調べることだけなので、10 回の反復後に停止します。

はじめに、強調を 200 に設定します。

rng default % for fair comparison
opts = statset('MaxIter',10);
YEX200 = tsne(X,'Algorithm','barneshut','NumPCAComponents',50,'Exaggeration',200,...
    'NumPrint',1,'Verbose',1,'Options',opts);

|==============================================|
|   ITER   | KL DIVERGENCE   | NORM GRAD USING |
|          | FUN VALUE USING | EXAGGERATED DIST|
|          | EXAGGERATED DIST| OF X            |
|          | OF X            |                 |
|==============================================|
|        1 |    2.190347e+03 |    6.078667e-05 |
|        2 |    2.190352e+03 |    4.769050e-03 |
|        3 |    2.204061e+03 |    9.423678e-02 |
|        4 |    2.464585e+03 |    2.113271e-02 |
|        5 |    2.501222e+03 |    2.616407e-02 |
|        6 |    2.529362e+03 |    3.022570e-02 |
|        7 |    2.553233e+03 |    3.108418e-02 |
|        8 |    2.562822e+03 |    3.278873e-02 |
|        9 |    2.538056e+03 |    3.222265e-02 |
|       10 |    2.504932e+03 |    3.671708e-02 |

最初の数回の反復ではカルバック・ライブラーダイバージェンスが増加しており、勾配のノルムも増加しています。

埋め込みの最終結果を調べるため、既定の停止条件を使用して、完了までアルゴリズムを実行できるようにします。

rng default % for fair comparison
YEX200 = tsne(X,'Algorithm','barneshut','NumPCAComponents',50,'Exaggeration',200);
figure
gscatter(YEX200(:,1),YEX200(:,2),L,clr)
title('Exaggeration 200')

この強調値では、明確にはクラスターに分離されません。

学習率が 100,000 の場合の初期動作を表示します。

rng default % for fair comparison
YL100k = tsne(X,'Algorithm','barneshut','NumPCAComponents',50,'LearnRate',1e5,...
    'NumPrint',1,'Verbose',1,'Options',opts);

|==============================================|
|   ITER   | KL DIVERGENCE   | NORM GRAD USING |
|          | FUN VALUE USING | EXAGGERATED DIST|
|          | EXAGGERATED DIST| OF X            |
|          | OF X            |                 |
|==============================================|
|        1 |    2.815885e+01 |    1.024049e-06 |
|        2 |    2.816002e+01 |    2.902059e-04 |
|        3 |    3.195873e+01 |    7.355889e-04 |
|        4 |    3.348151e+01 |    3.958901e-04 |
|        5 |    3.365935e+01 |    2.876905e-04 |
|        6 |    3.342462e+01 |    3.906245e-04 |
|        7 |    3.303205e+01 |    4.037983e-04 |
|        8 |    3.263320e+01 |    5.665630e-04 |
|        9 |    3.235384e+01 |    4.319099e-04 |
|       10 |    3.211238e+01 |    4.803526e-04 |

この場合も、最初の数回の反復ではカルバック・ライブラーダイバージェンスが増加しており、勾配のノルムも増加しています。

埋め込みの最終結果を調べるため、既定の停止条件を使用して、完了までアルゴリズムを実行できるようにします。

rng default % for fair comparison
YL100k = tsne(X,'Algorithm','barneshut','NumPCAComponents',50,'LearnRate',1e5);
figure
gscatter(YL100k(:,1),YL100k(:,2),L,clr)
title('Learning Rate 100,000')

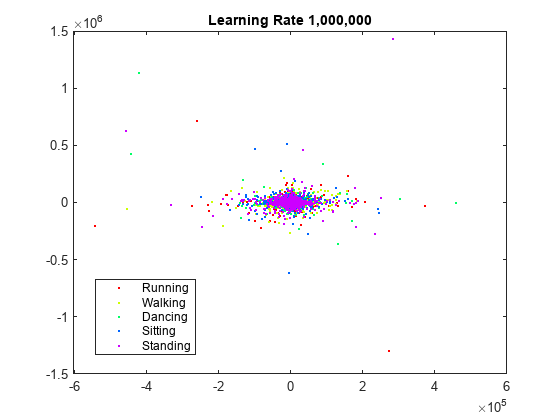
学習率が大きすぎるので、有用な埋め込みは得られません。

まとめ

既定設定の tsne は、クラスターが明確に定義された 2 次元の点に高次元の初期データを埋め込む処理を適切に行います。アルゴリズムの設定の影響を予測することは困難です。クラスタリングが改善されることもありますが、ほとんどの場合は既定設定が適切なようです。この調査に速度は含まれていませんが、設定がアルゴリズムの速度に影響を与える可能性があります。特にこのデータでは、Barnes-Hut アルゴリズムは著しく高速になります。

MNIST データを処理するコード

以下は、データをワークスペースに読み込む関数のコードです。

function [X,L] = processMNISTdata(imageFileName,labelFileName)

[fileID,errmsg] = fopen(imageFileName,'r','b');
if fileID < 0
    error(errmsg);
end
%%
% First read the magic number. This number is 2051 for image data, and
% 2049 for label data
magicNum = fread(fileID,1,'int32',0,'b');
if magicNum == 2051
    fprintf('\nRead MNIST image data...\n')
end
%%
% Then read the number of images, number of rows, and number of columns
numImages = fread(fileID,1,'int32',0,'b');
fprintf('Number of images in the dataset: %6d ...\n',numImages);
numRows = fread(fileID,1,'int32',0,'b');
numCols = fread(fileID,1,'int32',0,'b');
fprintf('Each image is of %2d by %2d pixels...\n',numRows,numCols);
%%
% Read the image data
X = fread(fileID,inf,'unsigned char');
%%
% Reshape the data to array X
X = reshape(X,numCols,numRows,numImages);
X = permute(X,[2 1 3]);
%%
% Then flatten each image data into a 1 by (numRows*numCols) vector, and 
% store all the image data into a numImages by (numRows*numCols) array.
X = reshape(X,numRows*numCols,numImages)';
fprintf(['The image data is read to a matrix of dimensions: %6d by %4d...\n',...
    'End of reading image data.\n'],size(X,1),size(X,2));
%%
% Close the file
fclose(fileID);
%%
% Similarly, read the label data.
[fileID,errmsg] = fopen(labelFileName,'r','b');
if fileID < 0
    error(errmsg);
end
magicNum = fread(fileID,1,'int32',0,'b');
if magicNum == 2049
    fprintf('\nRead MNIST label data...\n')
end
numItems = fread(fileID,1,'int32',0,'b');
fprintf('Number of labels in the dataset: %6d ...\n',numItems);

L = fread(fileID,inf,'unsigned char');
fprintf(['The label data is read to a matrix of dimensions: %6d by %2d...\n',...
    'End of reading label data.\n'],size(L,1),size(L,2));
fclose(fileID);

参考文献

[1] 元の NIST データセットから派生して作成された MNIST データセットの著作権は Yann LeCun (Courant Institute, NYU) と Corinna Cortes (Google Labs, New York) が有しています。MNIST データセットは、Creative Commons Attribution-Share Alike 3.0 ライセンス (https://creativecommons.org/licenses/by-sa/3.0/) の条件下で使用可能になります。