Main Content

ロジスティック回帰の正則化

スクリプトを開く

次の例では、二項回帰の正則化の方法を示します。二項回帰の既定の (基準) リンク関数はロジスティック関数です。

手順 1. データを準備する。

ionosphere データを読み込みます。応答 Y は 'g' または 'b' という文字から構成される cell 配列です。このセル配列を 'g' を表す true の論理値に変換します。X の最初の 2 列を削除するのは、処理の難しい統計プロパティが含まれているためです。このプロパティについては、本書では詳しく説明しません。

load ionosphere
Ybool = strcmp(Y,'g');
X = X(:,3:end);

手順 2. 交差検証による近似を作成する。

25 個の Lambda 値と 10 倍交差検証を使用して、正規化した二項回帰を作成します。この処理には数分かかることがあります。

rng('default') % for reproducibility
[B,FitInfo] = lassoglm(X,Ybool,'binomial',...
    'NumLambda',25,'CV',10);

手順 3. プロットを調べて適切な正則化を求める。

lassoPlot は標準トレース プロットと交差検証逸脱度プロットの両方を表示します。両方のプロットを調べます。

lassoPlot(B,FitInfo,'PlotType','CV');
legend('show','Location','best') % show legend

このプロットは、緑の円と破線の付いた最小逸脱度点を正則化パラメーター Lambda の関数として特定します。青い円で囲まれた点には、最小逸脱度に標準偏差が 1 つだけ加算されています。

lassoPlot(B,FitInfo,'PlotType','Lambda','XScale','log');

トレース プロットは、非ゼロのモデル係数を正則化パラメーター Lambda の関数として表示します。予測子と線形モデルが 32 個あるため、曲線も 32 個あります。Lambda が左に向かって増加しているため、lassoglm はさまざまな係数を 0 に設定してモデルから削除します。

トレース プロットは多少圧縮されています。拡大してもう少し細かく見てみます。

xlim([.01 .1])
ylim([-3 3])

Lambda がプロットの左側に向かって増加するにつれて、非ゼロの係数が少なくなります。

最小逸脱度に 1 つの標準偏差点を加え、Lambda 値で非ゼロのモデル係数の数を求めます。正則化モデル係数は、B 行列の FitInfo.Index1SE 列にあります。

indx = FitInfo.Index1SE;
B0 = B(:,indx);
nonzeros = sum(B0 ~= 0)

nonzeros =

    14

Lambda を FitInfo.Index1SE に設定すると、lassoglm は 32 ある元の予測子の半数以上を削除します。

手順 4. 正則化モデルを作成する。

定数項は FitInfo.Intercept ベクトルの FitInfo.Index1SE エントリ内にあります。この値を cnst と呼びます。

モデルは logit(mu) = log(mu/(1 - mu)) = X*B0 + cnst です。したがって、予測する場合 mu = exp(X*B0 + cnst)/(1+exp(x*B0 + cnst)) です。

関数 glmval はモデルの予測を評価します。この関数は、最初のモデル係数が定数項に関連しているものと想定しています。そのため、定数項をもつ係数ベクトルを最初に作成します。

cnst = FitInfo.Intercept(indx);
B1 = [cnst;B0];

手順 5. 残差を調べる。

正規化 lassoglm モデルのモデル予測に対して、学習データをプロットします。

preds = glmval(B1,X,'logit');
histogram(Ybool - preds) % plot residuals
title('Residuals from lassoglm model')

手順 6. 代替方法: 最小二乗一般化線形モデルで特定した予測子を使用する。

モデルから得たバイアスのある予測を使用する代わりに、特定した予測子のみを使用して、不偏のモデルを作成できます。

predictors = find(B0); % indices of nonzero predictors
mdl = fitglm(X,Ybool,'linear',...
    'Distribution','binomial','PredictorVars',predictors)

mdl = 


Generalized linear regression model:
    y ~ [Linear formula with 15 terms in 14 predictors]
    Distribution = Binomial

Estimated Coefficients:
                   Estimate       SE        tStat        pValue  
                   _________    _______    ________    __________

    (Intercept)      -2.9367    0.50926     -5.7666    8.0893e-09
    x1                 2.492    0.60795       4.099    4.1502e-05
    x3                2.5501    0.63304      4.0284     5.616e-05
    x4               0.48816    0.50336      0.9698       0.33215
    x5                0.6158    0.62192     0.99015        0.3221
    x6                 2.294     0.5421      4.2317    2.3198e-05
    x7               0.77842    0.57765      1.3476        0.1778
    x12               1.7808    0.54316      3.2786     0.0010432
    x16            -0.070993    0.50515    -0.14054       0.88823
    x20              -2.7767    0.55131     -5.0365    4.7402e-07
    x24               2.0212    0.57639      3.5067    0.00045372
    x25              -2.3796    0.58274     -4.0835    4.4363e-05
    x27              0.79564    0.55904      1.4232       0.15467
    x29               1.2689    0.55468      2.2876      0.022162
    x32              -1.5681    0.54336     -2.8859     0.0039035


351 observations, 336 error degrees of freedom
Dispersion: 1
Chi^2-statistic vs. constant model: 262, p-value = 1e-47

モデルの残差をプロットします。

plotResiduals(mdl)

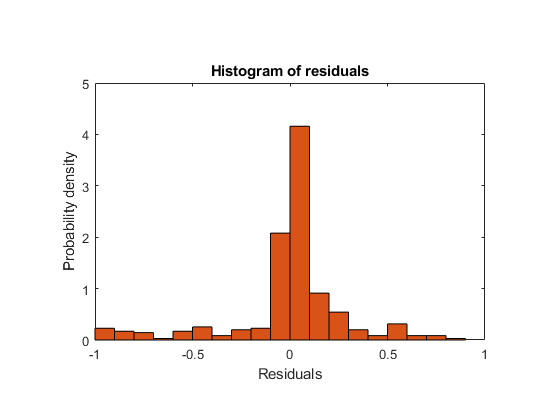
予想どおり、最小二乗モデルの残差は、正則化モデルの残差よりわずかに小さい値です。ただし、新しいデータに対して mdl がより適切な予測子であるということにはなりません。