並列計算を使用するブートストラップの実装
逐次または並列でのブートストラップ
ここでは、並列と逐次でブートストラップの時間を計測する例を示します。この例では、2 つのガウスの混合からデータを生成して結果として得られるデータのノンパラメトリックな推定を構築し、ブートストラップを使用してサンプリングの変化量がどのようなものであるかを予測します。
データを次のように生成します。
% Generate a random sample of size 1000, % from a mixture of two Gaussian distributions x = [randn(700,1); 4 + 2*randn(300,1)];
データからノンパラメトリックな密度推定を次のように構築します。
latt = -4:0.01:12; myfun = @(X) ksdensity(X,latt); pdfestimate = myfun(x);
サンプリングのばらつきを調べるために推定をブートストラップします。時間比較のために逐次でブートストラップを実行します。
tic;B = bootstrp(200,myfun,x);toc Elapsed time is 10.878654 seconds.
時間比較のために並列でブートストラップを実行します。
mypool = parpool() Starting parpool using the 'local' profile ... connected to 2 workers. mypool = Pool with properties: AttachedFiles: {0x1 cell} NumWorkers: 2 IdleTimeout: 30 Cluster: [1x1 parallel.cluster.Local] RequestQueue: [1x1 parallel.RequestQueue] SpmdEnabled: 1opt = statset('UseParallel',true); tic;B = bootstrp(200,myfun,x,'Options',opt);toc Elapsed time is 6.304077 seconds.この例では、並列計算が逐次計算との比較で 2 倍近く高速になることがわかります。
ksdensity の密度推定を並列ブートストラップで取得された 200 個のブートストラップ済み推定に重ねます。このプロットの密度推定の正確さを評価するための手がかりが得られます。
hold on
for i=1:size(B,1),
plot(latt,B(i,:),'c:')
end
plot(latt,pdfestimate);
xlabel('x');ylabel('Density estimate')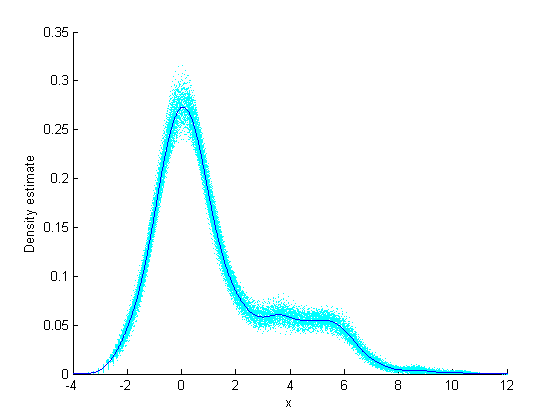
再現可能な並列ブートストラップ
再現可能な方法でこの例を並列実行するには、オプションを適切に設定します (再現性のある並列計算を実行するを参照)。まず、問題と並列環境を 逐次または並列でのブートストラップにあるように設定します。その後、サブストリームを使用するオプションと共に、サブストリームをサポートするストリームをオプションに設定します。
s = RandStream('mlfg6331_64'); % has substreams
opts = statset('UseParallel',true,...
'Streams',s,'UseSubstreams',true);
B2 = bootstrp(200,myfun,x,'Options',opts);ブートストラップを再度実行して同じ結果を得るには、次の手順を実行します。
reset(s) % set the stream to initial state
B3 = bootstrp(200,myfun,x,'Options',opts);
isequal(B2,B3) % check if same results
ans =
1