線形混合効果モデルのワークフロー
この例では、LME (線形混合効果モデル) の当てはめと解析の方法を説明します。
標本データを読み込みます。
load flu
データセット配列 flu には、変数 Date と、インフルエンザ推定罹患率 (Google® 検索から推定される 9 地域の値と CDC による全国の推定値) が格納されている 10 個の変数が含まれています。
データを再編成してプロットします。
線形混合効果モデルを当てはめるには、データが適切な形式の table になっていなければなりません。インフルエンザ羅患率を応答として使用することにより線形混合効果モデルを当てはめるには、地域に対応する 9 個の列を 1 つの配列にまとめます。新しいデータセット配列 flu2 には、応答変数 FluRate、各推定の元になっている地域を示すノミナル変数 Region、全国の推定値 WtdILI およびグループ化変数 Date が含まれなければなりません。
flu2 = stack(flu,2:10,'NewDataVarName','FluRate',... 'IndVarName','Region'); flu2.Date = nominal(flu2.Date);
flu2 を table として定義します。
flu2 = dataset2table(flu2);
インフルエンザ罹患率を全国の推定値に対してプロットします。
plot(flu2.WtdILI,flu2.FluRate,'ro') xlabel('WtdILI') ylabel('Flu Rate')
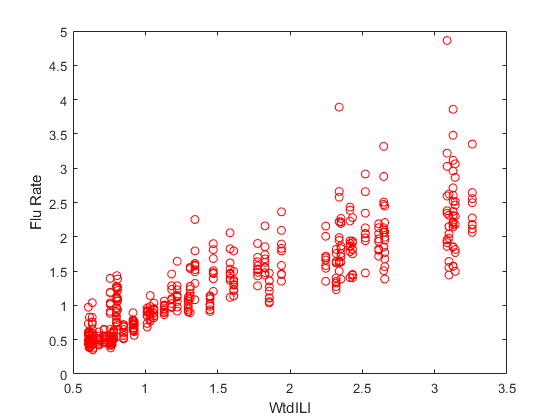
各地域のインフルエンザ罹患率は全国の推定値と直接的な関係があることがわかります。
LME モデルを当てはめ、結果を解釈します。
予測子変数としての全国の推定値と、Date で変化するランダム切片により、線形混合効果モデルを当てはめます。
lme = fitlme(flu2,'FluRate ~ 1 + WtdILI + (1|Date)')
lme =
Linear mixed-effects model fit by ML
Model information:
Number of observations 468
Fixed effects coefficients 2
Random effects coefficients 52
Covariance parameters 2
Formula:
FluRate ~ 1 + WtdILI + (1 | Date)
Model fit statistics:
AIC BIC LogLikelihood Deviance
286.24 302.83 -139.12 278.24
Fixed effects coefficients (95% CIs):
Name Estimate SE tStat DF pValue
{'(Intercept)'} 0.16385 0.057525 2.8484 466 0.0045885
{'WtdILI' } 0.7236 0.032219 22.459 466 3.0502e-76
Lower Upper
0.050813 0.27689
0.66028 0.78691
Random effects covariance parameters (95% CIs):
Group: Date (52 Levels)
Name1 Name2 Type Estimate
{'(Intercept)'} {'(Intercept)'} {'std'} 0.17146
Lower Upper
0.13227 0.22226
Group: Error
Name Estimate Lower Upper
{'Res Std'} 0.30201 0.28217 0.32324
0.0045885 および 3.0502e-76 という小さい 
値は、切片と全国の推定値の両方が有意であることを示しています。また、変量効果項 
の標準偏差の信頼限界 (0.13227, 0.22226) には、変量効果項が有意であることを示す 0 が含まれていません。
生の残差と近似値の対比をプロットします。
figure();
plotResiduals(lme,'fitted')
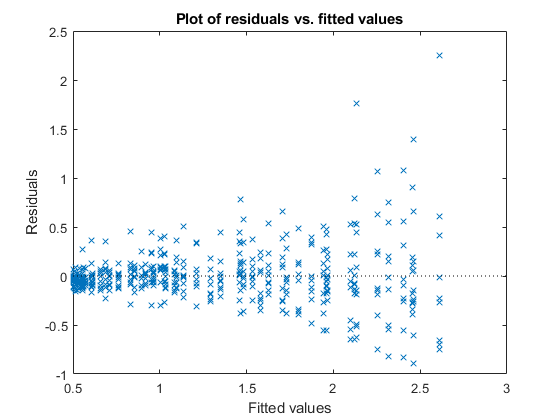
近似応答値の増加にともない残差の分散も増加します。この現象は不均一分散と呼ばれています。
外れ値のように右上に表示されている 2 件の観測値を検出します。
find(residuals(lme) > 1.5)
ans =
98
107
これらの観測値を削除して、モデルを再度当てはめます。
lme = fitlme(flu2,'FluRate ~ 1 + WtdILI + (1|Date)','Exclude',[98,107]);
モデルを改善します。
Date でグループ化された全国の推定値に独立したランダム項を含めると、モデルが改善されるか判定します。
altlme = fitlme(flu2,'FluRate ~ 1 + WtdILI + (1|Date) + (WtdILI-1|Date)',... 'Exclude',[98,107])
altlme =
Linear mixed-effects model fit by ML
Model information:
Number of observations 466
Fixed effects coefficients 2
Random effects coefficients 104
Covariance parameters 3
Formula:
FluRate ~ 1 + WtdILI + (1 | Date) + (WtdILI | Date)
Model fit statistics:
AIC BIC LogLikelihood Deviance
179.39 200.11 -84.694 169.39
Fixed effects coefficients (95% CIs):
Name Estimate SE tStat DF pValue
{'(Intercept)'} 0.17837 0.054585 3.2676 464 0.001165
{'WtdILI' } 0.70836 0.030594 23.153 464 2.123e-79
Lower Upper
0.0711 0.28563
0.64824 0.76849
Random effects covariance parameters (95% CIs):
Group: Date (52 Levels)
Name1 Name2 Type Estimate
{'(Intercept)'} {'(Intercept)'} {'std'} 0.16631
Lower Upper
0.12977 0.21313
Group: Date (52 Levels)
Name1 Name2 Type Estimate Lower
{'WtdILI'} {'WtdILI'} {'std'} 4.6782e-08 NaN
Upper
NaN
Group: Error
Name Estimate Lower Upper
{'Res Std'} 0.26691 0.24934 0.28572
WtdILI 項の標準偏差の推定値はほぼ 0 なので、信頼区間を計算できません。これは、モデルのパラメーターが多すぎ、(WtdILI-1|Date) 項が有意でないことを示しています。次のように compare メソッドを使用すると、これを正式に検定できます。compare(lme,altlme,'CheckNesting',true)。
地域別にグループ化された切片の変量効果項を初期モデル lme に追加します。
lme2 = fitlme(flu2,'FluRate ~ 1 + WtdILI + (1|Date) + (1|Region)',... 'Exclude',[98,107]);
lme モデルと lme2 モデルを比較します。
compare(lme,lme2,'CheckNesting',true)
ans =
THEORETICAL LIKELIHOOD RATIO TEST
Model DF AIC BIC LogLik LRStat deltaDF pValue
lme 4 177.39 193.97 -84.694
lme2 5 62.265 82.986 -26.133 117.12 1 0
0 という 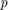値は、lme2 が lme より適切に当てはめられていることを示しています。
切片と全国平均に、相関する可能性のある変量効果項を追加すると、モデル lme2 が改善されるか確認します。
lme3 = fitlme(flu2,'FluRate ~ 1 + WtdILI + (1|Date) + (1 + WtdILI|Region)',... 'Exclude',[98,107])
lme3 =
Linear mixed-effects model fit by ML
Model information:
Number of observations 466
Fixed effects coefficients 2
Random effects coefficients 70
Covariance parameters 5
Formula:
FluRate ~ 1 + WtdILI + (1 | Date) + (1 + WtdILI | Region)
Model fit statistics:
AIC BIC LogLikelihood Deviance
13.338 42.348 0.33076 -0.66153
Fixed effects coefficients (95% CIs):
Name Estimate SE tStat DF pValue
{'(Intercept)'} 0.1795 0.054953 3.2665 464 0.0011697
{'WtdILI' } 0.70719 0.04252 16.632 464 4.6451e-49
Lower Upper
0.071514 0.28749
0.62363 0.79074
Random effects covariance parameters (95% CIs):
Group: Date (52 Levels)
Name1 Name2 Type Estimate
{'(Intercept)'} {'(Intercept)'} {'std'} 0.17634
Lower Upper
0.14093 0.22064
Group: Region (9 Levels)
Name1 Name2 Type Estimate
{'(Intercept)'} {'(Intercept)'} {'std' } 0.0077037
{'WtdILI' } {'(Intercept)'} {'corr'} -0.059604
{'WtdILI' } {'WtdILI' } {'std' } 0.088069
Lower Upper
3.2362e-16 1.8338e+11
-0.99996 0.99995
0.051694 0.15004
Group: Error
Name Estimate Lower Upper
{'Res Std'} 0.20976 0.19568 0.22486
地域 (Region) 別にグループ化された切片に関する変量効果項の標準偏差の推定値は 0.0077037 で、信頼区間が非常に大きく、0 が含まれています。これは、地域別にグループ化された切片の変量効果が有意でないことを示しています。切片と WtdILI の間で変量効果の相関は -0.059604 です。この相関の信頼区間も非常に大きく、0 が含まれています。これは、相関が有意でないことを示しています。
(1 + WtdILI | Region) 変量効果項から切片を削除して、モデルを再度当てはめます。
lme3 = fitlme(flu2,'FluRate ~ 1 + WtdILI + (1|Date) + (WtdILI - 1|Region)',... 'Exclude',[98,107])
lme3 =
Linear mixed-effects model fit by ML
Model information:
Number of observations 466
Fixed effects coefficients 2
Random effects coefficients 61
Covariance parameters 3
Formula:
FluRate ~ 1 + WtdILI + (1 | Date) + (WtdILI | Region)
Model fit statistics:
AIC BIC LogLikelihood Deviance
9.3395 30.06 0.33023 -0.66046
Fixed effects coefficients (95% CIs):
Name Estimate SE tStat DF pValue
{'(Intercept)'} 0.1795 0.054892 3.2702 464 0.0011549
{'WtdILI' } 0.70718 0.042486 16.645 464 4.0496e-49
Lower Upper
0.071637 0.28737
0.62369 0.79067
Random effects covariance parameters (95% CIs):
Group: Date (52 Levels)
Name1 Name2 Type Estimate
{'(Intercept)'} {'(Intercept)'} {'std'} 0.17633
Lower Upper
0.14092 0.22062
Group: Region (9 Levels)
Name1 Name2 Type Estimate Lower
{'WtdILI'} {'WtdILI'} {'std'} 0.087925 0.054474
Upper
0.14192
Group: Error
Name Estimate Lower Upper
{'Res Std'} 0.20979 0.19585 0.22473
新しいモデル lme3 の項はすべて有意です。
lme2 と lme3 を比較します。
compare(lme2,lme3,'CheckNesting',true,'NSim',100)
ans =
SIMULATED LIKELIHOOD RATIO TEST: NSIM = 100, ALPHA = 0.05
Model DF AIC BIC LogLik LRStat pValue
lme2 5 62.265 82.986 -26.133
lme3 5 9.3395 30.06 0.33023 52.926 0.009901
Lower Upper
0.00025064 0.053932
0.009901 という 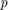値は、lme3 が lme2 より適切に当てはめられていることを示しています。
2 次固定効果項をモデル lme3 に追加します。
lme4 = fitlme(flu2,'FluRate ~ 1 + WtdILI^2 + (1|Date) + (WtdILI - 1|Region)',... 'Exclude',[98,107])
lme4 =
Linear mixed-effects model fit by ML
Model information:
Number of observations 466
Fixed effects coefficients 3
Random effects coefficients 61
Covariance parameters 3
Formula:
FluRate ~ 1 + WtdILI + WtdILI^2 + (1 | Date) + (WtdILI | Region)
Model fit statistics:
AIC BIC LogLikelihood Deviance
6.7234 31.588 2.6383 -5.2766
Fixed effects coefficients (95% CIs):
Name Estimate SE tStat DF pValue
{'(Intercept)'} -0.063406 0.12236 -0.51821 463 0.60456
{'WtdILI' } 1.0594 0.16554 6.3996 463 3.8232e-10
{'WtdILI^2' } -0.096919 0.0441 -2.1977 463 0.028463
Lower Upper
-0.30385 0.17704
0.73406 1.3847
-0.18358 -0.010259
Random effects covariance parameters (95% CIs):
Group: Date (52 Levels)
Name1 Name2 Type Estimate
{'(Intercept)'} {'(Intercept)'} {'std'} 0.16732
Lower Upper
0.13326 0.21009
Group: Region (9 Levels)
Name1 Name2 Type Estimate Lower
{'WtdILI'} {'WtdILI'} {'std'} 0.087865 0.054443
Upper
0.1418
Group: Error
Name Estimate Lower Upper
{'Res Std'} 0.20979 0.19585 0.22473
0.028463 という 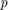値は、2 次項 WtdILI^2 の係数が有意であることを示しています。
観測された応答と残差に対して、近似された応答をプロットします。
F = fitted(lme4); R = response(lme4); figure(); plot(R,F,'rx') xlabel('Response') ylabel('Fitted')
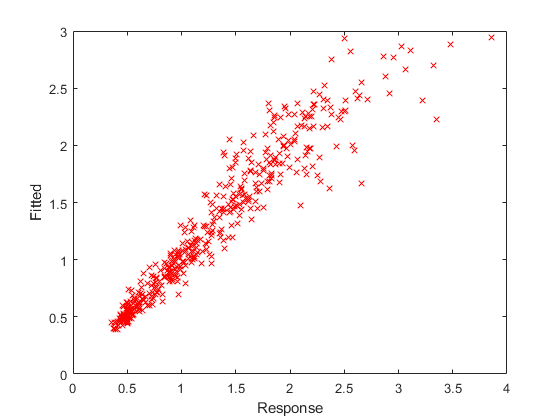
観測された応答と比較すると、近似された応答の値の角度がほぼ 45 度になります。これは近似の精度が高いことを意味します。
残差と近似値の対比をプロットします。
figure();
plotResiduals(lme4,'fitted')
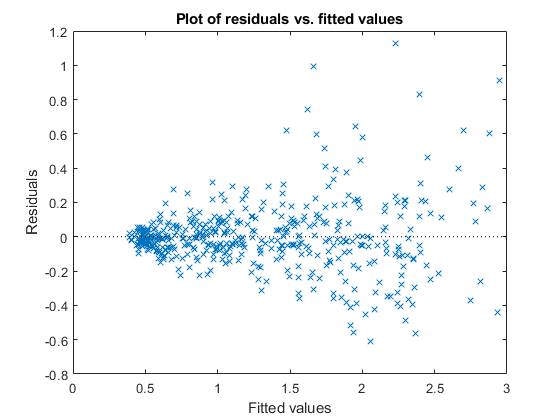
モデルは改善されていますが、まだ不均一分散が認識されます。原因として、データ セットに存在しない (つまり、モデルに存在しない) 別の予測子が考えられます。
2005 年 11 月 6 日の ENCentral 地域における近似されたインフルエンザ罹患率を特定します。
F(flu2.Region == 'ENCentral' & flu2.Date == '11/6/2005')
ans =
1.4860
応答値を無作為に生成します。
全国推定値が 1.625 で、MidAtl 地域および 2006 年 4 月 23 日に対する応答値を無作為に生成します。最初に新しい table を定義します。日付と地域は元の table でノミナルであるため、新しい table でも同様に定義しなければなりません。
tblnew.Date = nominal('4/23/2006'); tblnew.WtdILI = 1.625; tblnew.Region = nominal('MidAtl'); tblnew = struct2table(tblnew);
次に、応答値を生成します。
random(lme4,tblnew)
ans =
1.2679
