主成分分析を使用した直交回帰の近似

ライブスクリプトを開く

この例では、主成分分析 (PCA) により線形回帰を近似する方法を示します。PCA は、データから近似モデルまでの垂直距離を最小化します。この分析は、直交回帰、全最小二乗、デミング回帰、変数誤差などと呼ばれるものの線形バージョンであり、予測子変数と応答変数の間に自然な区分がない場合、またはすべての変数が誤差を含んで測定される場合に適しています。これは、予測子変数が正確に測定され、応答変数のみが誤差成分をもつ、通常の回帰仮定とは対照的なものです。

たとえば、2 つのデータベクトル x と y がある場合は、各ポイント (x(i), y(i)) から直線までの垂直距離を最小化する直線を近似できます。さらに一般的な例としては、p 観測変数を使用して、p 次元空間で r 次元超平面を近似できます (r < p)。r の選択は、PCA で保持するための成分の数を選択することに相当します。つまり、予測誤差に基づく選択の場合もあれば、管理しやすい次元数までデータを縮小するという実際的な選択の場合もあります。

この例では、観測される 3 つの変数に関するデータを使用して、平面と直線を近似します。これと同じことは、任意の数の変数、および任意の次元のモデルに対して容易に実行できます。ただし、高次元で近似を可視化することは、明らかに単純ではありません。

3 次元データへの平面の当てはめ

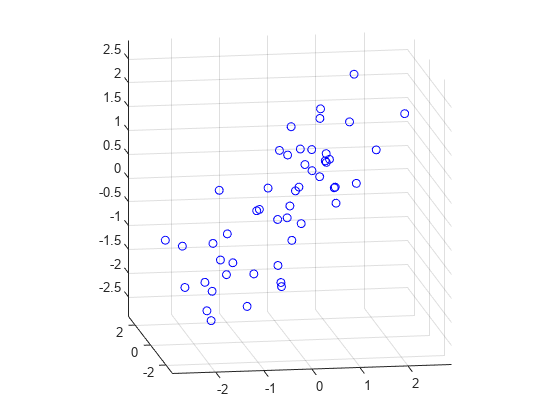
まず、三変量法線データを例として生成します。変数のうちの 2 つは非常に緊密に相関されています。

rng(5,'twister');
X = mvnrnd([0 0 0], [1 .2 .7; .2 1 0; .7 0 1],50);
plot3(X(:,1),X(:,2),X(:,3),'bo');
grid on;
maxlim = max(abs(X(:)))*1.1;
axis([-maxlim maxlim -maxlim maxlim -maxlim maxlim]);
axis square
view(-9,12);

Figure contains an axes object. The axes contains a line object which displays its values using only markers.

次に、PCA を使用して平面をデータに当てはめます。最初の 2 つの主成分の係数によって、平面の基底を形成するベクトルが定義されます。3 番目の PC は最初の 2 つの PC と直交しており、その係数によって平面の法線ベクトルが定義されます。

[coeff,score,roots] = pca(X);
basis = coeff(:,1:2)

basis = 3×2

    0.6774   -0.0790
    0.2193    0.9707
    0.7022   -0.2269

normal = coeff(:,3)

normal = 3×1

    0.7314
   -0.0982
   -0.6749

近似の説明はこれですべてです。それでは、結果を詳しく考察して、データと共に近似をプロットしてみましょう。

最初の 2 つの成分は 2 次元で可能な限り多くの分散について説明しているので、平面はデータに対する最良の 2 次元線形近似になっています。同様に、3 番目の成分はデータ内の最小量の分散について説明しており、回帰における誤差項になっています。PCA からの特性根 (固有値) は、各成分の説明分散の量を定義します。

pctExplained = roots' ./ sum(roots)

pctExplained = 1×3

    0.6226    0.2976    0.0798

主成分スコアの最初の 2 つの座標は、平面に対する各ポイントの投影を、平面の座標系で表しています。オリジナル座標系における近似ポイントの座標を取得するには、各 PC 係数ベクトルをそれに対応するスコアで乗算して、データの平均値を加算します。残差は、オリジナルデータから近似ポイントを差し引いたものになります。

[n,p] = size(X);
meanX = mean(X,1);
Xfit = repmat(meanX,n,1) + score(:,1:2)*coeff(:,1:2)';
residuals = X - Xfit;

Xfit の各近似ポイントによって満たされる近似された平面の方程式は、([x1 x2 x3] - meanX)*normal = 0 です。平面はポイント meanX を通過し、原点までの垂直距離は meanX*normal になります。X の各ポイントから平面までの垂直距離、つまり残差のノルムは、各中心点と平面に対する法線とのドット積です。近似された平面は、二乗誤差の合計を最小化します。

error = abs((X - repmat(meanX,n,1))*normal);
sse = sum(error.^2)

sse = 
15.5142

近似を可視化するには、平面、オリジナルデータ、および平面に対するオリジナルデータの投影をプロットします。

[xgrid,ygrid] = meshgrid(linspace(min(X(:,1)),max(X(:,1)),5), ...
                         linspace(min(X(:,2)),max(X(:,2)),5));
zgrid = (1/normal(3)) .* (meanX*normal - (xgrid.*normal(1) + ygrid.*normal(2)));
h = mesh(xgrid,ygrid,zgrid,'EdgeColor',[0 0 0],'FaceAlpha',0);

hold on
above = (X-repmat(meanX,n,1))*normal < 0;
below = ~above;
nabove = sum(above);
X1 = [X(above,1) Xfit(above,1) nan*ones(nabove,1)];
X2 = [X(above,2) Xfit(above,2) nan*ones(nabove,1)];
X3 = [X(above,3) Xfit(above,3) nan*ones(nabove,1)];
plot3(X1',X2',X3','-', X(above,1),X(above,2),X(above,3),'o', 'Color',[0 .7 0]);
nbelow = sum(below);
X1 = [X(below,1) Xfit(below,1) nan*ones(nbelow,1)];
X2 = [X(below,2) Xfit(below,2) nan*ones(nbelow,1)];
X3 = [X(below,3) Xfit(below,3) nan*ones(nbelow,1)];
plot3(X1',X2',X3','-', X(below,1),X(below,2),X(below,3),'o', 'Color',[1 0 0]);

hold off
maxlim = max(abs(X(:)))*1.1;
axis([-maxlim maxlim -maxlim maxlim -maxlim maxlim]);
axis square
view(-9,12);

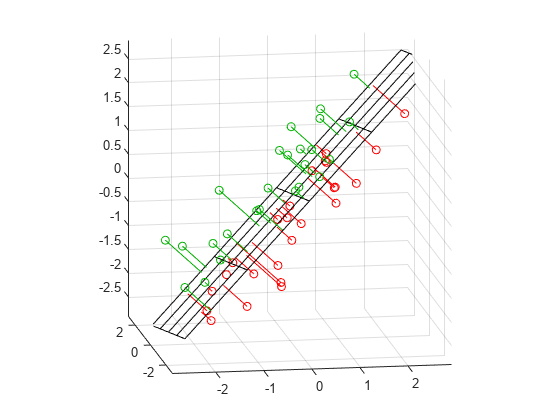
Figure contains an axes object. The axes object contains 53 objects of type surface, line. One or more of the lines displays its values using only markers

緑のポイントは平面の上、赤いポイントは平面の下になります。

3 次元データへの直線の当てはめ

これよりさらに簡単なのがデータへの直線の当てはめです。また、PCA には入れ子特性があるため、既に計算された成分を使用できます。直線を定義する方向ベクトルは、最初の主成分の係数によって指定されます。2 番目と 3 番目の PC は最初の PC と直交し、これらの PC の係数によって、直線に対する垂直方向が定義されます。直線を描くための最も簡単な方程式は meanX + t*dirVect です。ここで、t は直線に沿った位置をパラメーター表現します。

dirVect = coeff(:,1)

dirVect = 3×1

    0.6774
    0.2193
    0.7022

主成分スコアの最初の座標は、直線に対する各ポイントの投影を表します。2 次元近似の場合と同様に、スコアで乗算される PC 係数ベクトルは、オリジナル座標系における近似ポイントを指定します。

Xfit1 = repmat(meanX,n,1) + score(:,1)*coeff(:,1)';

直線、オリジナルデータ、および直線に対するオリジナルデータの投影をプロットします。

t = [min(score(:,1))-.2, max(score(:,1))+.2];
endpts = [meanX + t(1)*dirVect'; meanX + t(2)*dirVect'];
plot3(endpts(:,1),endpts(:,2),endpts(:,3),'k-');

X1 = [X(:,1) Xfit1(:,1) nan*ones(n,1)];
X2 = [X(:,2) Xfit1(:,2) nan*ones(n,1)];
X3 = [X(:,3) Xfit1(:,3) nan*ones(n,1)];
hold on
plot3(X1',X2',X3','b-', X(:,1),X(:,2),X(:,3),'bo');
hold off
maxlim = max(abs(X(:)))*1.1;
axis([-maxlim maxlim -maxlim maxlim -maxlim maxlim]);
axis square
view(-9,12);
grid on

Figure contains an axes object. The axes object contains 52 objects of type line. One or more of the lines displays its values using only markers

このプロット内の多くの投影は直線に対して垂直になっていないように見えますが、これは 3 次元データを 2 次元でプロットしようとしているためです。実稼動時の MATLAB® の Figure ウィンドウでは、プロットをさまざまな視点に対話形式で回転することで、投影が実際に垂直であることを確認したり、直線とデータの近似の度合いを把握したりすることができます。