最小二乗法を使用する指数分布での近似

「最小二乗法」という用語は、回帰直線または回帰曲面で近似して、応答変数を 1 つまたは複数の予測子変数の関数としてモデル化する際によく使用されます。ここでは、最小二乗法をこれとは非常に異なる仕方で適用する方法を説明します。つまり、変数が 1 つしかない一変量分布近似という方法です。

最初に、いくつかの標本データをシミュレートします。指数分布を使用してデータを生成します。この例では、実際の場合と同様に、データが特定のモデルに由来することは知られていないものとします。

rng(37,'twister');
n = 100;
x = exprnd(2,n,1);

次に、データの経験累積分布関数 (ECDF) を計算します。これは、各データ ポイント x で 1/n の累積確率 p に急な変動がある単純なステップ関数です。

x = sort(x);
p = ((1:n)-0.5)' ./ n;
stairs(x,p,'k-');
xlabel('x');
ylabel('Cumulative probability (p)');

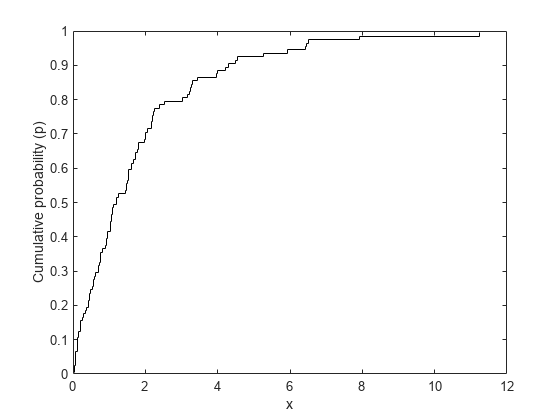
指数分布を使用してこれらのデータを近似します。その 1 つの方法は、累積分布関数 (CDF) がデータの ECDF を (後で説明する意味において) 最もよく近似する指数分布を見つけることです。指数 CDF は、 p = Pr{X <= x} = 1 - exp(-x/mu) です。これを -log(1-p)*mu = x に変換すると、-log(1-p) と x との間の線形関係が得られます。データが指数分布に由来する場合、ECDF から計算した x と p の値をこの方程式に代入すると、少なくとも近似的には線形関係が認められるはずです。最小二乗法を使用して、原点から x 対 -log(1-p) まで直線で近似すると、その近似直線はデータに "最も近い" 指数分布を表すことになります。直線の傾きは、パラメーター mu の推定値です。

同様に、y = -log(1-p) を標準の (平均値 1) 指数分布の "理想化された標本" と見なすことができます。これらの理想化された値は、確率のスケール上で正確に等間隔に配置されます。データが指数分布に由来する場合には、x と y の Q-Q プロットは、ほぼ線形になるはずです。したがって、最小二乗法直線で原点から x 対 y までを近似します。

y = -log(1 - p);
muHat = y \ x

muHat =

    1.8627

データと近似直線をプロットします。

plot(x,y,'+', y*muHat,y,'r--');
xlabel('x');
ylabel('y = -log(1-p)');

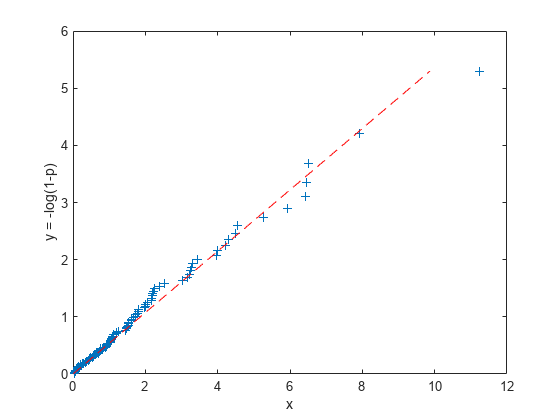
この線形近似により、水平つまり "x 軸" 方向の誤差の二乗和が最小になることに注意してください。これは、y = -log(1-p) の値が決定性の値であり、無作為なのは x の値だからです。また、y 対 x の回帰推定を行ったり、他の種類の線形近似を使用したりすることもできます。たとえば、加重回帰、直交回帰、さらにはロバスト回帰などです。ただし、ここではこれらの可能性は調べません。

比較のため、最尤法でデータを近似します。

muMLE = expfit(x)

muMLE =

    1.7894

いよいよここで、2 つの推定分布を未変換の累積確率スケール上にプロットします。

stairs(x,p,'k-');
hold on
xgrid = linspace(0,1.1*max(x),100)';
plot(xgrid,expcdf(xgrid,muHat),'r--', xgrid,expcdf(xgrid,muMLE),'b--');
hold off
xlabel('x'); ylabel('Cumulative Probability (p)');
legend({'Data','LS Fit','ML Fit'},'location','southeast');

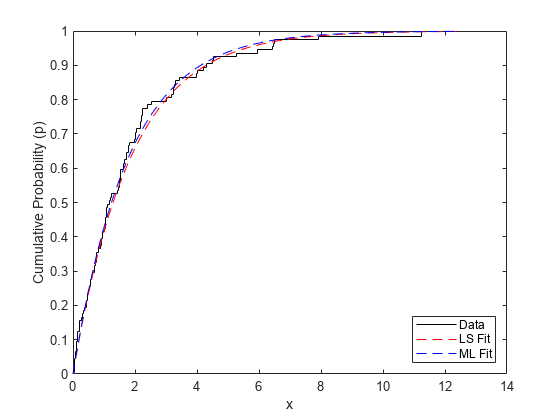
この 2 つの方法で非常によく似た分布が得られます。もっとも、LS 近似は分布の裾での観測の影響をより強く受けています。

ワイブル分布の近似

もう少し複雑な例として、ワイブル分布の標本データをシミュレートし、x の ECDF を計算します。

n = 100;
x = wblrnd(2,1,n,1);
x = sort(x);
p = ((1:n)-0.5)' ./ n;

これらのデータをワイブル分布で近似するには、ワイブル分布の CDF が p = Pr{X <= x} = 1 - exp(-(x/a)^b) であることに注意してください。これを log(a) + log(-log(1-p))*(1/b) = log(x) に変換すると、線形関係が再度得られますが、今回は log(-log(1-p)) と log(x) との間の線形関係になります。最小二乗法を使用して、ECDF の x と p を使用して変換されたスケール上に直線で近似することができます。すると、直線の傾きと切片から a と b の推定値を得ることができます。

logx = log(x);
logy = log(-log(1 - p));
poly = polyfit(logy,logx,1);
paramHat = [exp(poly(2)) 1/poly(1)]

paramHat =

    2.1420    1.0843

データと近似直線を変換されたスケール上にプロットします。

plot(logx,logy,'+', log(paramHat(1)) + logy/paramHat(2),logy,'r--');
xlabel('log(x)');
ylabel('log(-log(1-p))');

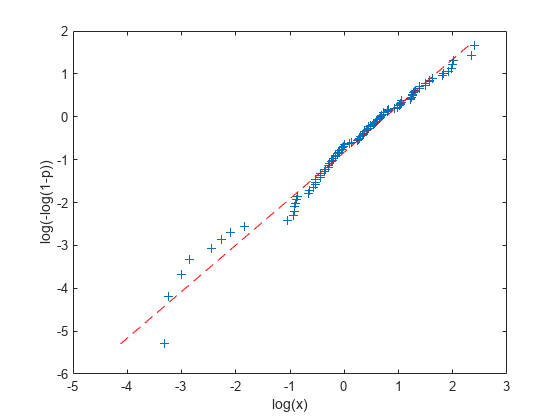
比較のため、最尤法でデータを近似します。そして、2 つの推定分布を変換されていないスケール上にプロットします。

paramMLE = wblfit(x)
stairs(x,p,'k');
hold on
xgrid = linspace(0,1.1*max(x),100)';
plot(xgrid,wblcdf(xgrid,paramHat(1),paramHat(2)),'r--', ...
     xgrid,wblcdf(xgrid,paramMLE(1),paramMLE(2)),'b--');
hold off
xlabel('x'); ylabel('Cumulative Probability (p)');
legend({'Data','LS Fit','ML Fit'},'location','southeast');

paramMLE =

    2.1685    1.0372

しきい値パラメーターの例

しきい値パラメーターが 1 つあるワイブル分布や対数正規分布などの正の分布で近似しなければならないことがあります。たとえば、あるワイブル確率変数が (0,Inf) を超える値を取り、あるしきい値パラメーター c がその範囲を (c,Inf) に移すとします。このしきい値パラメーターが既知である場合は、話は簡単です。ところが、未知の場合には推定しなければなりません。これらのモデルを最尤法で近似するのは困難です。尤度に複数の最頻値が存在したり、データにとって理にかなっていないパラメーター値に対しては、不定になることもあるからです。そのため、最尤法は適さないことがよくあります。しかし、最小二乗法の手順にさらに手順を少し加えるだけで、安定した推定値を得ることができます。

実例を示すため、しきい値が 1 つある 3 パラメーター ワイブル分布のデータをシミュレートします。前の例と同様に、データが特定のモデルに由来することは知られておらず、しきい値も未知であるとします。

n = 100;
x = wblrnd(4,2,n,1) + 4;
hist(x,20); xlim([0 16]);

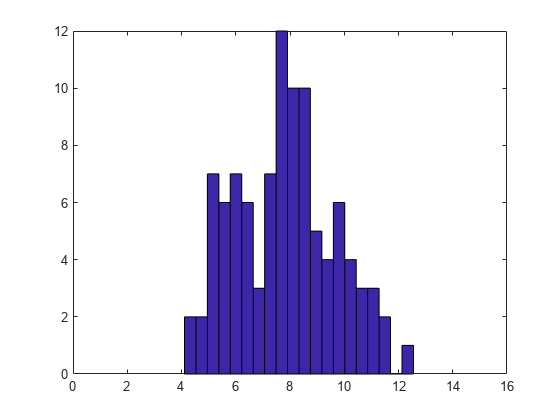
これらのデータを 3 パラメーター ワイブル分布で近似するにはどうすればよいでしょうか。しきい値がたとえば 1 であることがわかっていれば、データからその値を引いてから最小二乗法の手順を使用して、ワイブル分布の形状とスケール パラメーターを推定することができます。

x = sort(x);
p = ((1:n)-0.5)' ./ n;
logy = log(-log(1-p));
logxm1 = log(x-1);
poly1 = polyfit(log(-log(1-p)),log(x-1),1);
paramHat1 = [exp(poly1(2)) 1/poly1(1)]
plot(logxm1,logy,'b+', log(paramHat1(1)) + logy/paramHat1(2),logy,'r--');
xlabel('log(x-1)');
ylabel('log(-log(1-p))');

paramHat1 =

    7.4305    4.5574

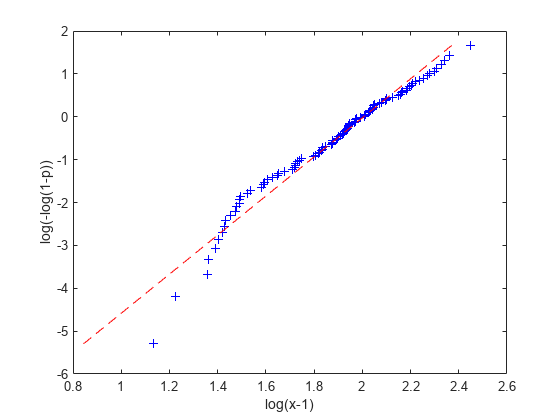
これは、あまり良い近似ではありません。log(x-1) と log(-log(1-p)) には線形関係がありません。もちろんこれは、正確なしきい値を知らないからです。しきい値をさまざまに変えて引き算すると、それに応じてさまざまなプロットとパラメーター推定値を得ることができます。

logxm2 = log(x-2);
poly2 = polyfit(log(-log(1-p)),log(x-2),1);
paramHat2 = [exp(poly2(2)) 1/poly2(1)]

paramHat2 =

    6.4046    3.7690

logxm4 = log(x-4);
poly4 = polyfit(log(-log(1-p)),log(x-4),1);
paramHat4 = [exp(poly4(2)) 1/poly4(1)]

paramHat4 =

    4.3530    1.9130

plot(logxm1,logy,'b+', logxm2,logy,'r+', logxm4,logy,'g+', ...
     log(paramHat1(1)) + logy/paramHat1(2),logy,'b--', ...
     log(paramHat2(1)) + logy/paramHat2(2),logy,'r--', ...
     log(paramHat4(1)) + logy/paramHat4(2),logy,'g--');
xlabel('log(x - c)');
ylabel('log(-log(1 - p))');
legend({'Threshold = 1' 'Threshold = 2' 'Threshold = 4'}, 'location','northwest');

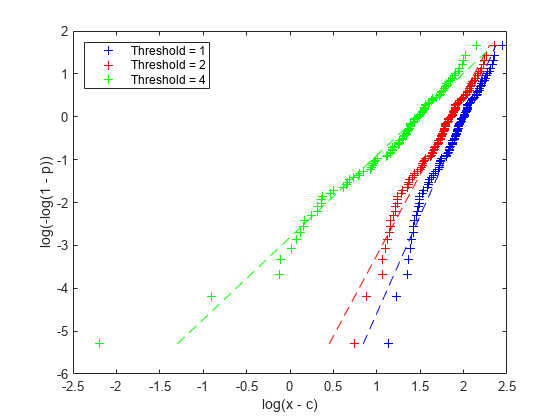
log(x-4) と log(-log(1-p)) との間の関係は、ほぼ線形に見えます。正しいしきい値パラメーターを引き算するとほぼ線形プロットになるはずなので、これは、しきい値は 4 であると考えるのが理にかなっていることの証拠です。一方、しきい値を 2 および 3 とした場合のプロットは、線形からのズレが一貫して大きくなります。これは、これらの値ではデータとの整合性が取れないことの証拠です。

この引数を形式化することができます。しきい値パラメーターの各暫定値の場合、対応する暫定ワイブル近似値を変換された変数 log(x-c) と log(-log(1-p)) 上で線形回帰の R^2 値を最大化するパラメーター値と見なすことができます。しきい値パラメーターを推定するには、その 1 手順をさらに実行して、可能なしきい値すべてに対して R^2 値を最大化します。

r2 = @(x,y) 1 - norm(y - polyval(polyfit(x,y,1),x)).^2 / norm(y - mean(y)).^2;
threshObj = @(c) -r2(log(-log(1-p)),log(x-c));
cHat = fminbnd(threshObj,.75*min(x), .9999*min(x));
poly = polyfit(log(-log(1-p)),log(x-cHat),1);
paramHat = [exp(poly(2)) 1/poly(1) cHat]
logx = log(x-cHat);
logy = log(-log(1-p));
plot(logx,logy,'b+', log(paramHat(1)) + logy/paramHat(2),logy,'r--');
xlabel('log(x - cHat)');
ylabel('log(-log(1 - p))');

paramHat =

    4.7448    2.3839    3.6029

非 location-scale ファミリ

指数分布は scale ファミリの一種であり、対数スケールではワイブル分布は location-scale ファミリの一種なので、この最小二乗法はこの 2 つのケースでは明快でした。location-scale 分布で近似する一般的な手順は、次のとおりです。

追加のしきい値パラメーターが 1 つある location-scale ファミリである分布で近似することが、ほんのわずかに難しいことを知りました。

しかし、location-scale ファミリでない他の分布 (ガンマ分布など) は、少し面倒です。線形関係が得られる CDF の変換はありません。ただし、同じような考えを適用することはできます。今回は、未変換の累積確率スケールを改良します。その近似手順を可視化するには、P-P プロットが適切な方法です。

ECDF の経験的確率が、パラメトリック モデルの近似確率にプロットされる場合、0 から 1 に向かって 1:1 直線上の狭い範囲でばらつきます。これは、パラメーター値が観測データをよく説明する分布を定義することを示しています。なぜなら、近似された CDF は経験的 CDF をよく近似するからです。考え方は、確率プロットを 1:1 直線にできるだけ近づけるパラメーター値を見つける、ということです。分布がデータの良いモデルではない場合、これはそもそも不可能かもしれません。P-P プロットが 1:1 直線から一貫して離れる場合には、モデルに疑問の余地があるかもしれません。ただし、これらのプロットの点は独立しているわけではないので、解釈は回帰残差プロットとまったく同じにはならないことを忘れないでください。

たとえば、データをシミュレートして、ガンマ分布で近似します。

n = 100;
x = gamrnd(2,1,n,1);

x の ECDF を計算します。

x = sort(x);
pEmp = ((1:n)-0.5)' ./ n;

ガンマ分布のパラメーターの初期推定値、たとえば a=1 と b=1 を使用して、確率プロットを作成することができます。この推定値はあまり良いものではありません。パラメトリックな CDF の確率は、ECDF の確率に近くありません。a と b の値を変えて試すと、P-P プロット上のばらつき具合および 1:1 直線との相違の程度もそれに応じて変わります。この例では a と b の正しい値がわかっているので、その値を試してみましょう。

a0 = 1; b0 = 1;
p0Fit = gamcdf(x,a0,b0);
a1 = 2; b1 = 1;
p1Fit = gamcdf(x,a1,b1);
plot([0 1],[0 1],'k--', pEmp,p0Fit,'b+', pEmp,p1Fit,'r+');
xlabel('Empirical Probabilities');
ylabel('(Provisionally) Fitted Gamma Probabilities');
legend({'1:1 Line','a=1, b=1', 'a=2, b=1'}, 'location','southeast');

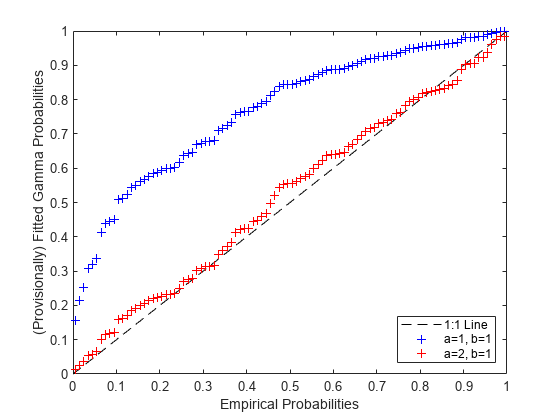
a と b の値の 2 番目の集合だと、プロットがはるかに良くなるので、P-P プロットがどれほど直線に近いのかで "適合性" を判定している場合には、データにより適合していると言えます。

ばらつき具合を 1:1 直線にできるだけ一致させるには、1:1 直線との距離の重み付き二乗和を最小にする a と b の値を見つけます。重みは経験的確率に関して定義され、プロットの中央で最低、端点で最高になります。これらの重みは、近似確率の分散を埋め合わせます。分散は、中央付近で最高、裾で最低になります。この重み付き最小二乗法により、a と b の推定量が決まります。

wgt = 1 ./ sqrt(pEmp.*(1-pEmp));
gammaObj = @(params) sum(wgt.*(gamcdf(x,exp(params(1)),exp(params(2)))-pEmp).^2);
paramHat = fminsearch(gammaObj,[log(a1),log(b1)]);
paramHat = exp(paramHat)

paramHat =

    2.2759    0.9059

pFit = gamcdf(x,paramHat(1),paramHat(2));
plot([0 1],[0 1],'k--', pEmp,pFit,'b+');
xlabel('Empirical Probabilities');
ylabel('Fitted Gamma Probabilities');

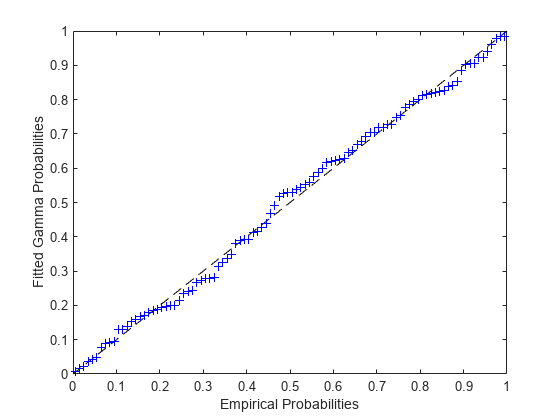
以前に考慮した location-scale のケースでは、単一の直線近似で分布を近似できたことに注意してください。ここでは、しきい値パラメーターの例と同様に、最適近似パラメーター値を反復して見つけなければなりませんでした。

モデルの指定ミス

P-P プロットは、さまざまな分布ファミリの近似を比較する際にも便利です。これらのデータを対数正規分布で近似するとどうなるでしょうか。

wgt = 1 ./ sqrt(pEmp.*(1-pEmp));
LNobj = @(params) sum(wgt.*(logncdf(x,params(1),exp(params(2)))-pEmp).^2);
mu0 = mean(log(x)); sigma0 = std(log(x));
paramHatLN = fminsearch(LNobj,[mu0,log(sigma0)]);
paramHatLN(2) = exp(paramHatLN(2))

paramHatLN =

    0.5331    0.7038

pFitLN = logncdf(x,paramHatLN(1),paramHatLN(2));
hold on
plot(pEmp,pFitLN,'rx');
hold off
ylabel('Fitted Probabilities');
legend({'1:1 Line', 'Fitted Gamma', 'Fitted Lognormal'},'location','southeast');

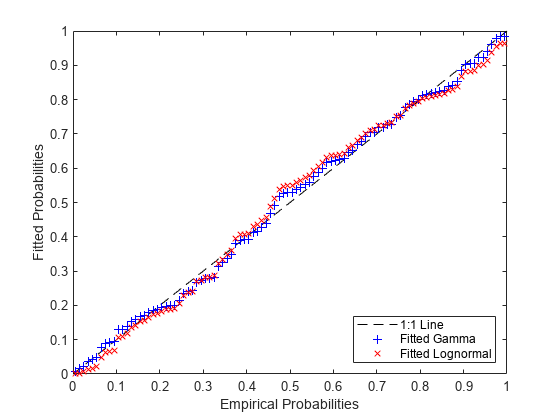
対数正規近似が裾でガンマ近似からどれほど一貫して離れているのかに注意してください。左側の裾ではよりゆっくり成長し、右側の裾ではよりゆっくり消滅します。ガンマ分布の方がデータの近似度がわずかに高いようです。

対数正規しきい値パラメーターの例

対数正規分布は、最尤法により簡単に近似することができます。いったんデータに対数変換が適用されると、最尤法は正規分布を近似することと等価であるからです。しかし、対数正規モデルでもしきい値パラメーターを推定しなければならないこともあります。そのようなモデルの尤度は有界でないので、最尤法ではうまくいきません。ところが、最小二乗法なら推定することができます。2 パラメーター対数正規分布は、location-scale ファミリに対数変換することができるので、前述のしきい値パラメーターがあるワイブル分布で近似する例と同じ手順を踏むことができます。ただし、ここでは、ガンマ分布で近似した前の例と同様に、累積確率スケール上で推定します。

実例を示すため、しきい値が 1 つある 3 パラメーター対数正規分布のデータをシミュレートします。

n = 200;
x = lognrnd(0,.5,n,1) + 10;
hist(x,20); xlim([8 15]);

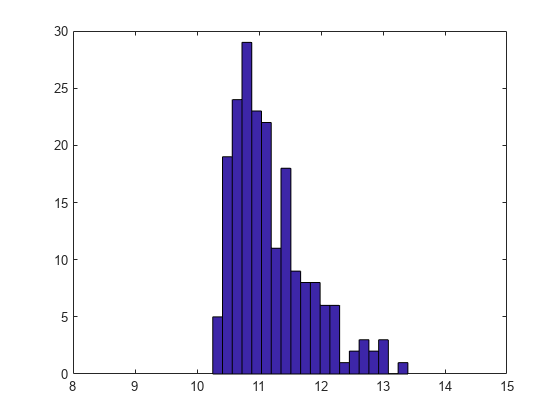
x の ECDF を計算し、最適な 3 パラメーター対数正規分布のパラメーターを見つけます。

x = sort(x);
pEmp = ((1:n)-0.5)' ./ n;
wgt = 1 ./ sqrt(pEmp.*(1-pEmp));
LN3obj = @(params) sum(wgt.*(logncdf(x-params(3),params(1),exp(params(2)))-pEmp).^2);
c0 = .99*min(x);
mu0 = mean(log(x-c0)); sigma0 = std(log(x-c0));
paramHat = fminsearch(LN3obj,[mu0,log(sigma0),c0]);
paramHat(2) = exp(paramHat(2))

paramHat =

   -0.0698    0.5930   10.1045

pFit = logncdf(x-paramHat(3),paramHat(1),paramHat(2));
plot(pEmp,pFit,'b+', [0 1],[0 1],'k--');
xlabel('Empirical Probabilities');
ylabel('Fitted 3-param Lognormal Probabilities');

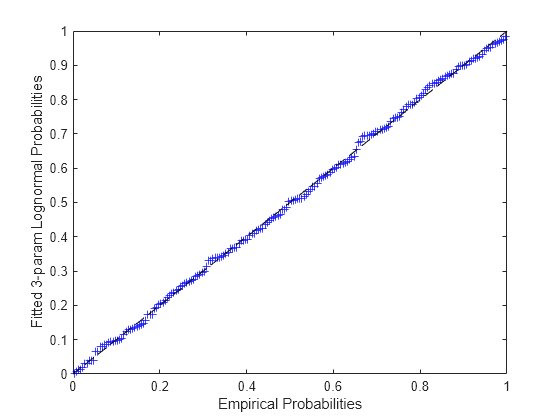
精度の尺度

パラメーターの推定は、話の一部にすぎません。モデル近似には推定値、特に標準誤差の精度を評価することも必要です。最尤法では、情報行列と大きい標本の漸近引数を使用して、標本抽出を繰り返して推定量の共分散行列の近似値を求めるのが一般的です。最小二乗法の推定量には、そのような理論はありません。

ただし、モンテ カルロ シミュレーションには、標準誤差を推定するための別の方法があります。近似モデルを使用してデータセットを多数生成すると、モンテ カルロ標準偏差で推定量の標準誤差の近似値を求めることができます。簡単にするため、近似関数を別のファイル logn3fit.m に定義しておきました。

estsSim = zeros(1000,3);
for i = 1:size(estsSim,1)
    xSim = lognrnd(paramHat(1),paramHat(2),n,1) + paramHat(3);
    estsSim(i,:) = logn3fit(xSim);
end
std(estsSim)

ans =

    0.1542    0.0908    0.1303

推定値の分布を調べること、近似的正規性の仮定がこの標本サイズにとって理にかなっているかどうかをチェックすること、またはバイアスがないかどうかをチェックすることも役立つかもしれません。

subplot(3,1,1), hist(estsSim(:,1),20);
title('Log-Location Parameter Bootstrap Estimates');
subplot(3,1,2), hist(estsSim(:,2),20);
title('Log-Scale Parameter Bootstrap Estimates');
subplot(3,1,3), hist(estsSim(:,3),20);
title('Threshold Parameter Bootstrap Estimates');

明らかに、しきい値パラメーターの推定量は歪んでいます。これは想定内のことです。推定量は最小データ値によって上に有界だからです。他の 2 つのヒストグラムも、近似的正規性が最初のヒストグラムの log-location パラメーターにとって疑わしい仮定である可能性があることを示しています。上記で計算した標準誤差を解釈するに当たっては、この点を念頭に置いておかなければなりません。そして、log-location パラメーターとしきい値パラメーターについては、信頼区間を通常の方法で構築することは適切ではない可能性があります。

シミュレートされた推定値の平均値は、シミュレートされたデータを生成するために使用されるパラメーター値に近い値になります。これは、この手順がこの標本サイズで少なくとも推定値に近いパラメーター値に関してはほぼ不偏であることを示しています。

[paramHat; mean(estsSim)]

ans =

   -0.0698    0.5930   10.1045
   -0.0690    0.5926   10.0905

最後になりますが、関数 bootstrp を使用して、ブートストラップ標準誤差推定値を計算することもできました。この値は、データについて何のパラメーター仮定も行いません。

estsBoot = bootstrp(1000,@logn3fit,x);
std(estsBoot)

ans =

    0.1490    0.0785    0.1180

ブートストラップ標準誤差は、モンテ カルロ計算値から大きく外れてはいません。これは当然です。近似モデルがデータ例の生成元モデルと同じであるからです。

まとめ

ここで説明した近似法は、最尤法では役立つパラメーター推定値を得られない場合に一変量分布で近似するために使用できる最尤法の代替法の 1 つです。1 つの重要な適用法は、しきい値パラメーターが関係する分布 (3 パラメーター対数正規など) で近似することです。最尤法の推定値の場合には、標準誤差の計算がより難しくなります。これは、解析的近似法が存在しないからです。もっとも、シミュレーションにより、実行可能な代替法を得ることができます。

近似法を実演で示すためにここで使用した P-P プロットは、一変量分布で近似しようとしても近似が存在しないことを視覚的に示すものとして、それ単独でも便利なものです。