レーダー検出可能性係数のモデル化

R2021a 以降

この例では、レーダーレンジ方程式の詳細な解析のためにアンテナ、送信機、受信機のゲインと損失をモデル化する方法を示します。まず、レーダー方程式の SNR 形式を使用して、レーダー受信機で利用可能な S/N 比 (SNR) を計算します。次に、検出可能性係数を、指定された検出確率 $P_{d}$ と偽警報の確率 $P_{f a}$ で検出を行うために必要なしきい値 SNR として定義します。次に、システムの最大レンジを、利用可能な SNR がこの検出可能性係数と等しくなるレンジ (指定された $P_{d}$ と $P_{f a}$ での検出が依然として可能な最大レンジ) として推定します。この例では、レーダーシステムのさまざまなコンポーネントによってもたらされる損失が推定最大レンジに与える影響をさらに調べます。まず、利用可能な SNR に対する感度時間制御 (STC) とエクリプスの影響について検討します。次に、レーダー検出可能性係数を増やす必要があるスキャンおよび信号処理の損失について検討します。この例では、最後に検出器出力で結果の $P_{d}$ を計算し、損失がレーダーシステムの検出性能に与える影響を示します。

利用可能な SNR

レーダー方程式は、レーダーシステムの主なパラメーターを組み合わせ、レーダーエンジニアがレーダーシステムの最大検出レンジ、必要なピーク送信電力、または利用可能な最大 SNR を計算できるようにします。レーダー方程式は通常、これら 3 つの主要なパフォーマンス特性の 1 つにそれぞれ対応する比較的単純な数式の集合です。レンジ $R$ で利用可能な最大 SNR を計算するためのレーダー方程式の一般的な形式は次のとおりです。

$S N R = \frac{P_{t} τ G_{t} G_{r} λ^{2} σ}{(4 π)^{3} k T_{s} R^{4} L}$

ここで、

$P_{t}$ はピーク送信電力

$τ$ は送信パルス幅

$G_{t}$ は送信アンテナゲイン

$G_{r}$ は受信アンテナゲイン

$λ$ はレーダーの波長

$σ$ はレーダーターゲット断面積 (RCS)

$k$ はボルツマン定数

$T_{s}$ はシステムノイズ温度

$L$ は送信機-ターゲット-受信機パスにおいて受信信号エネルギーを低下させる損失を組み合わせた一般的な損失係数です。

ターゲットレンジと RCS を除く右辺のすべてのパラメーターは、レーダーデザイナーが制御します。この方程式は、レンジ $R$ に位置する特定サイズのターゲットに対して、送信電力を増やしたり、アンテナのサイズを大きくしたり、周波数を低くしたり、受信機の感度を上げたりすることで、受信機で利用可能な SNR を高めることができることを示しています。

3 GHz の周波数で動作する S 帯域空港監視レーダーを考えます。ピーク送信電力は 0.2 MW、送信および受信アンテナゲインは 34 dB、パルス持続時間は 11 $μ$ s、ノイズ指数は 4.1 dB です。レーダーは、100 km の最大レンジ $R_{m}$ で 1 m $^{2}$ RCS のターゲットを検出する必要があるものとします。

lambda = freq2wavelen(3e9);         % Wavelength (m)
Pt = 0.2e6;                         % Peak power (W)
tau = 1.1e-5;                       % Pulse width (s)
G = 34;                             % Transmit and receive antenna gain (dB)
Ts = systemp(4.1);                  % System temperature (K) 
rcs = 1;                            % Target radar cross section (m^2)
Rm = 100e3;                         % Required maximum range (m)

まず、損失がない ( $L$ = 0 dB) と仮定します。レーダー方程式を使用し、受信機で利用可能な SNR をターゲットレンジの関数として計算します。

L = 0;                              % Combined transmission line and propagation losses (dB)
R = (1:40:130e3).';                 % Range samples (m)
SNR = radareqsnr(lambda,R,Pt,tau,'Gain',G,'Ts',Ts,'RCS',rcs,'Loss',L);

必要な最大レンジ 100 km で利用可能な SNR を計算します。

SNRatRm = SNR(find(R>=Rm,1))

SNRatRm = 
18.3169

計算された利用可能な SNR とともに最大レンジ要件をプロットします。

radarmetricplot(R*1e-3,SNR,'MetricName','Available SNR','MaxRangeRequirement',Rm*1e-3,...
    'RangeUnit','km','MetricUnit','dB','RadarName',{'Surveillance Radar'});
legend('Location','best');

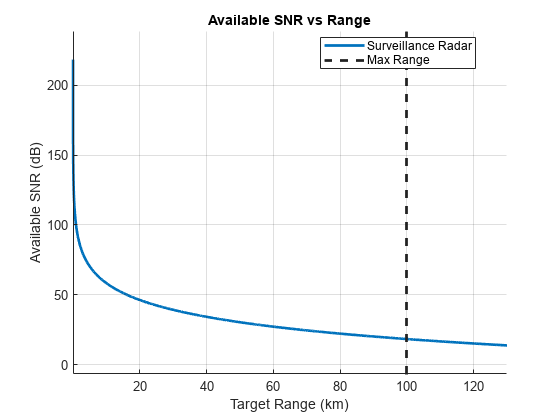
Figure contains an axes object. The axes object with title Available SNR vs Range, xlabel Target Range (km), ylabel Available SNR (dB) contains 2 objects of type line, constantline. These objects represent Surveillance Radar, Max Range.

必要な SNR

計算された利用可能な SNR は、検出を行えるほど高いでしょうか。レーダー受信機によって処理される信号は、送信された波形とランダムノイズの組み合わせであるため、この質問への答えは、目的の検出確率 $P_{d}$ と偽警報の最大許容確率 $P_{f a}$ によって決まります。これらの確率は、検出可能性係数 (検出可能性) とも呼ばれる必要な SNR を定義します。検出可能性係数は、指定された検出確率と偽警報の確率で検出を宣言するために必要な最小 SNR です。これは、RCS 変動と検出器の種類によっても異なります。 $P_{d}$ = 0.9 および $P_{f a}$ = 1e-6 と仮定し、二乗検出器によって定常 (Swerling 0) ターゲットから受信した単一パルスの検出可能性係数を計算します。

Pd = 0.9;
Pfa = 1e-6;
D0 = detectability(Pd,Pfa,1,'Swerling0')

D0 = 
13.1217

現実世界のターゲットに対するより正確なモデルである Swerling 1 変動ターゲットの検出可能性係数を計算します。Swerling 1 ターゲットについては、単一パルス検出可能性係数は大幅に高くなります。

D1 = detectability(Pd,Pfa,1,'Swerling1')

D1 = 
21.1436

結果として必要な SNR は利用可能な SNR よりも高くなります。つまり Swerling 1 ターゲットは単一のパルスでは検出されません。検出可能性係数を下げる一般的な方法は、パルス積分を実行することです。 $N$ = 10 個の非コヒーレント統合パルスについて検出可能性係数を計算します。

N = 10;
DN = detectability(Pd,Pfa,N,'Swerling1')

DN = 
13.5033

これは利用可能な SNR よりも低くなっています。したがって、10 個のパルスの非コヒーレント統合の後、このレーダーシステムは、検出確率 0.9、偽警報の確率 1e-6 で、必要な最大レンジ 100 km における 1 m $^{2}$ のターゲットを検出できるようになります。

Swerling 1 ターゲットと $N$ 個のパルスに対して計算された検出可能性係数は、積分ゲインと変動損失の影響を組み合わせたものです。積分ゲインは、単一のパルスを使用して定常ターゲットを検出するために必要な SNR と、 $N$ 個のパルスを使用して定常ターゲットを検出するために必要な SNR の差です。

Gi = detectability(Pd,Pfa,1,'Swerling0') - detectability(Pd,Pfa,N,'Swerling0')

Gi = 
7.7881

変動損失は、変動ターゲットを検出するのに必要な SNR と、定常ターゲットを検出するのに必要な SNR の差です。

Lf = detectability(Pd,Pfa,N,'Swerling1') - detectability(Pd,Pfa,N,'Swerling0')

Lf = 
8.1696

radarbudgetplot 関数を使用して、検出可能性係数の成分を示します。

radarbudgetplot([D0 -Gi Lf], {'Single-pulse steady target','Pulse integration gain','Fluctuation loss'});
title('Detectability Factor')

Figure contains an axes object. The axes object with title Detectability Factor, ylabel Required SNR (dB) contains 10 objects of type line, patch, text. These objects represent Detectability Factor, Losses, Gains.

システムの実際の最大レンジを評価するには、検出可能性係数を最小必要 SNR としてレーダー方程式のレンジ形式に代入します。

radareqrng(lambda,DN,Pt,tau,'Gain',G,'Ts',Ts,'RCS',rcs,'Loss',L,'unitstr','km')

ans = 
131.9308

目的の $P_{d}$ と最大許容 $P_{f a}$ による検出がどのレンジで可能であるかを明確に示すために、計算された検出可能性係数を SNR 対レンジのプロットに水平線として追加します。また、計算された検出可能性に基づいてレンジと SNR レベルを色分けするために、ストップライトチャートも使用します。利用可能な SNR 曲線が緑色のゾーンを通過するレンジではレーダーは検出要件を満たしますが、赤色のゾーンにあるレンジでは指定された $P_{d}$ および $P_{f a}$ での検出ができません。

radarmetricplot(R*1e-3,SNR,DN, ...
    'MetricName','Available SNR', ...
    'RequirementName','Detectability', ...
    'MaxRangeRequirement',Rm*1e-3, ...
    'RangeUnit','km','MetricUnit','dB', ...
    'ShowStoplight',true, ...
    'RadarName',{'Surveillance Radar'});
title([{'Available SNR vs Range'}, {'(No Losses)'}]);
legend('Location','best');

Figure contains an axes object. The axes object with title Available SNR vs Range (No Losses), xlabel Target Range (km), ylabel Available SNR (dB) contains 6 objects of type patch, line, constantline. These objects represent Pass, Fail, Surveillance Radar, Detectability, Max Range.

必要な最大レンジを超えるすべてのレンジは緑色で表示され、合格としてマークされます。

この解析では損失がゼロであると想定しているため、実際のレーダーシステムのレンジを適切に予測することはできません。指定されたパラメーターをもつ実際のレーダーシステムでは、次の理由により最大レンジが短くなります。

地球の表面と大気によって引き起こされる伝播の影響。これらの影響により、受信機で利用可能な信号エネルギーの量が減少します。
レーダーシステム全体で発生するさまざまな損失。このカテゴリの一部の損失は利用可能な SNR を低下させますが、他の損失は検出可能性係数を増加させます。

次のセクションでは、第 2 カテゴリに属する損失がレーダーシステムのレンジ性能に与える影響について詳しく検討します。

レンジ依存係数

監視レーダーシステムを設計する場合、受信機で利用可能な信号エネルギーの減少を考慮して、レーダー方程式にいくつかの要素を含める必要があります。

エクリプス

パルスレーダーシステムでは、パルス送信中に受信機がオフにされます。したがって、レーダーから 1 パルス長以内のレンジ、または明瞭レンジの周囲 1 パルス長以内のレンジから到達するターゲットエコーは、送信パルスによって食され、その結果、パルスの一部のみが受信され、処理されることになります。この例で検討するレーダーシステムのパルス幅は 11 $μ s$ です。完全なパルスを受信できる最も近いレンジは、最小レンジ $R_{m i n}$ です。

Rmin = time2range(tau)

Rmin = 
1.6489e+03

1649 m より近いターゲットからのエコーは、パルス送信が完了する前に到着します。明瞭レンジの倍数またはその付近に位置するターゲットでも同様の影響が見られます。パルス繰り返し周波数が 1350 Hz (パルス繰り返し間隔 $T \approx$ 0.75 ms) であると仮定して、システムの明瞭レンジを計算します。

prf = 1350;                         % Pulse repetition frequency
Rua = time2range(1/prf)

Rua = 
1.1103e+05

レンジ $R_{u a} \pm R_{m i n}$ から到着するエコーは、次の送信パルスによって食されます。次の図はパルスエクリプスを示しています。矢印はパルスの先端を示しています。

エクリプスにより、利用可能な SNR は 0 のレンジで深いノッチをもち、レンジは $R_{u a}$ の倍数に等しくなります。パルスエクリプスによる利用可能な SNR の損失を考慮するために、レーダー方程式にエクリプスファクターを追加します。

Du = tau*prf;                       % Duty cycle
Fecl = eclipsingfactor(R,Du,prf);   % Eclipsing factor

SNR = radareqsnr(lambda,R,Pt,tau,'Gain',G,'Ts',Ts,'RCS',rcs,'CustomFactor',Fecl,'Loss', L);

radarmetricplot(R*1e-3,SNR,DN, ...
    'MetricName','Available SNR', ...
    'RequirementName','Detectability', ...
    'MaxRangeRequirement',Rm*1e-3, ...
    'RangeUnit','km','MetricUnit','dB', ...
    'ShowStoplight',true, ...
    'RadarName',{'Surveillance Radar'});
title([{'Available SNR vs Range'}, {'(With Eclipsing)'}]);
legend('Location','best');

Figure contains an axes object. The axes object with title Available SNR vs Range (With Eclipsing), xlabel Target Range (km), ylabel Available SNR (dB) contains 6 objects of type patch, line, constantline. These objects represent Pass, Fail, Surveillance Radar, Detectability, Max Range.

現実世界のレーダーシステムでは、エクリプス損失を防ぎ、システムの明瞭レンジを拡大するために、PRF ダイバーシティが活用されています。

感度時間制御 (STC)

一般的な監視レーダーシステムは、長いレンジでターゲットを検出するためにかなりの量の電力を送信しなければなりません。利用可能なエネルギーはレンジとともに急速に減少しますが、非常に近いレンジでは、ピーク送信電力が高いため、小さなターゲットでも非常に強いリターンが発生する可能性があります。小さく不都合なターゲット (鳥、昆虫) からのこのような強いリターンは望ましくない検出につながる可能性がある一方で、通常サイズのターゲットや近くのクラッターが受信機を飽和させる可能性もあります。このような不都合な検出を回避することは、監視レーダーシステムにおいて特に望ましいと言えます。この問題を解決するために、レーダーシステムは STC を使用します。ターゲットがレーダーに近づくと一定の信号強度を維持するために、受信機のゲインをカットオフレンジ $R_{s t c}$ までスケールアップさせます。

Rstc = 60e3;                        % STC cutoff range (m)
Xstc = 4;                           % STC exponent selected to maintain target detectability at ranges below Rstc (since the signal power is inversely proportional to R^4)
Fstc = stcfactor(R,Rstc,Xstc);      % STC factor

SNR = radareqsnr(lambda,R,Pt,tau,'Gain',G,'Ts',Ts,'RCS',rcs,'CustomFactor',Fecl+Fstc,'Loss',L);

radarmetricplot(R*1e-3,SNR,DN, ...
    'MetricName','Available SNR', ...
    'RequirementName','Detectability', ...
    'MaxRangeRequirement',Rm*1e-3, ...
    'RangeUnit','km','MetricUnit','dB', ...
    'ShowStoplight',true, ...
    'RadarName',{'Surveillance Radar'});
title([{'Available SNR vs Range'}, {'(With STC and Eclipsing for 1 m^2 Target)'}]);
legend('Location','best');
ylim([-30 30])

Figure contains an axes object. The axes object with title Available SNR vs Range (With blank STC blank and blank Eclipsing blank for blank 1 blank m Squared baseline blank Target), xlabel Target Range (km), ylabel Available SNR (dB) contains 6 objects of type patch, line, constantline. These objects represent Pass, Fail, Surveillance Radar, Detectability, Max Range.

STC 係数を追加した後のプロットは、1 m $^{2}$ RCS ターゲットは最大レンジ $R_{m}$ までどこでも検出される一方、RCS が 0.03 m $^{2}$ の小さなターゲットは、どのレンジにおいても必要な 0.9 の $P_{d}$ に到達できず、拒否されることを示しています。

SNRsmallRCS = radareqsnr(lambda,R,Pt,tau,'Gain',G,'Ts',Ts,'RCS',0.03,'CustomFactor',Fecl+Fstc,'Loss',L);

radarmetricplot(R*1e-3,SNRsmallRCS,DN, ...
    'MetricName','Available SNR', ...
    'RequirementName','Detectability', ...
    'MaxRangeRequirement',Rm*1e-3, ...
    'RangeUnit','km','MetricUnit','dB', ...
    'ShowStoplight',true, ...
    'RadarName',{'Surveillance Radar'});
title([{'Available SNR vs Range'}, {'(With STC and Eclipsing for 0.03 m^2 Target)'}]);
legend('Location','best');
ylim([-30 20])

Figure contains an axes object. The axes object with title Available SNR vs Range (With blank STC blank and blank Eclipsing blank for blank 0 . 03 blank m Squared baseline blank Target), xlabel Target Range (km), ylabel Available SNR (dB) contains 6 objects of type patch, line, constantline. These objects represent Pass, Fail, Surveillance Radar, Detectability, Max Range.

これらのプロットから、STC は利用可能な SNR を、指定されたカットオフレンジまで拡大するのみであり、対象となる最大レンジでの利用可能な SNR には影響を与えないことがわかります。

スキャン

レーダーシステムは、アンテナを機械的に回転させるか、フェーズドアレイアンテナを使用して電子スキャンを実行することによって、検索ボリュームをスキャンできます。アンテナビームの不完全な形状と、検索ボリューム全体にわたってビームをスイープするプロセスにより、システムにさらなる損失が発生します。

ビーム形状損失

レーダー方程式では、受信した各パルスが最大振幅をもつと仮定して、アンテナゲインのピーク値を使用します。実際には、ビームがターゲットを通過すると、受信パルスはアンテナスキャンの双方向パターンによって変調され、ビーム形状が失われます。この損失の正確な値を計算するには、正確なアンテナパターンを知る必要があります。この情報は、この種の解析が通常実行されるレーダーシステム設計の初期段階では入手できない可能性があります。代わりに、典型的な実用アンテナのメインローブ形状は、ガウス形状で十分に近似できます。レーダーシステムが空間領域で高密度サンプリングを実行すると仮定し (ビームの移動は半電力ビーム幅の 0.71 未満)、1 次元スキャンのビーム形状損失を計算します。

Lb = beamloss

Lb = 
1.2338

レーダーシステムが方位角と仰角の両方でスキャンする場合、ビーム形状の損失は 2 倍になります。

beamloss(true)

ans = 
2.4677

スキャンセクター損失

この例では、レーダーシステムが電子制御フェーズドアレイを使用してスキャンを実行するものと仮定します。フェーズドアレイアンテナを使用すると、次の 2 つの影響によって、必要な SNR が増加します。1) ビーム方向の投影アレイ面積の減少によるビームの広がり、および 2) オフブロードサイド角度における個々のアレイ要素の有効開口面積の減少。これらの影響を考慮するには、スキャンセクター損失を検出可能性係数に追加します。例のシステムは方位角方向のみをスキャンし、スキャンセクターの範囲は -60 ～ 60 度であると仮定します。結果として生じる損失を計算します。

theta = [-60 60];
Larray = arrayscanloss(Pd,Pfa,N,theta,'Swerling1')

Larray = 
2.7745

信号処理

検出の前に、受信したレーダーエコーはレーダー信号処理チェーンを通過しなければなりません。信号処理チェーン内のさまざまなコンポーネントの目的は、必要な検出確率および偽警報の確率を保証し、クラッターからの不要なエコーを除去し、可変ノイズまたは非ガウスノイズを考慮することです。さらに、監視レーダーシステムにおいて考慮しなければならない信号処理損失のいくつかの要素についても検討します。

MTI

ムービングターゲットインジケーター (MTI) は、固定の、またはゆっくり移動するクラッターを除去し、高速で移動するターゲットからのエコーを通過させるプロセスです。一般的な MTI では、2 パルス、3 パルス、または 4 パルスのキャンセラーを使用してハイパスフィルターを実装し、ドップラーシフトが低いエコーを除去します。受信信号を MTI パルスキャンセラーに渡すと、ノイズサンプル間に相関関係が生じます。これにより、インテグレーションに使用できる独立したノイズサンプルの総数が減り、MTI ノイズ相関の損失が発生します。さらに、MTI キャンセラーは、周波数応答の null に近い速度をもつターゲットを大幅に抑制するため、追加の MTI 速度応答損失を引き起こします。2 パルスキャンセラーが使用されていると仮定して、MTI 損失のこれら 2 つの成分を計算します。

m = 2;
[Lmti_a, Lmti_b] = mtiloss(Pd,Pfa,N,m,'Swerling1')

Lmti_a = 
1.4468

Lmti_b = 
8.1562

単一の PRF を使用するシステムでは、検出に求められる高い確率に対して、MTI 速度応答損失が非常に高くなる可能性があります。この損失を排除するために、実際のレーダーシステムではほぼ常に PRF ダイバーシティが使用されます。

バイナリインテグレーション

バイナリインテグレーションは、M/N 統合とも呼ばれる、準最適非コヒーレント統合手法です。受信したパルス $N$ 個のうち $M$ 個が所定のしきい値を超えると、ターゲットが存在すると宣言されます。バイナリインテグレーターは比較的単純な自動検出器であり、ターゲットエコーとともに存在する可能性のある単一の大きな干渉パルスの影響をあまり受けません。したがって、バックグラウンドノイズまたはクラッターが非ガウスである場合、バイナリインテグレーターはさらにロバストになります。バイナリインテグレーションは準最適手法であるため、最適非コヒーレント統合と比較するとバイナリインテグレーション損失が発生します。 $M$ の最適値は感度の高い選択ではなく、最適値と大きく異なる場合でも重大なペナルティが生じないため、バイナリインテグレーション損失は 1.4 dB 未満に抑えることが可能です。 $N$ が 10 で、 $M$ が 6 に設定されているときのバイナリインテグレーション損失を計算します。

M = 6;
Lbint = binaryintloss(Pd,Pfa,N,M)

Lbint = 
1.0549

binaryintloss 関数は、定常 (Swerling 0) ターゲットを想定して損失を計算します。変動損失は検出可能性係数に含まれているため、変動するターゲットの場合にも同じバイナリインテグレーション損失計算を使用できます。

CFAR

定誤警報率 (CFAR) 検出器は、ノイズレベルまたは干渉レベルが変化するときに、ターゲットの誤検出率をほぼ一定に維持するために使用されます。CFAR は有限個の参照セルを平均してノイズレベルを推定するため、この推定値には誤差が生じ、これが CFAR 損失につながります。CFAR 損失とは、ノイズレベルが未知である場合に CFAR を使用して目的の検出パフォーマンスを達成するために必要な SNR が、既知のノイズレベルをもつ固定しきい値と比較して増加することです。合計 120 個のセルがセル平均化 CFAR に使用されると仮定して CFAR 損失を計算します。

Nrc = 120;
Lcfar = cfarloss(Pfa,Nrc)

Lcfar = 
0.2500

有効検出可能性係数

スキャンと信号処理の損失は、検出可能性係数を増大させます。これは、検出を行うためにより多くのエネルギーが必要になることを意味します。これらすべての損失の影響を含めた結果として得られる検出可能性係数を、有効検出可能性係数と呼びます。radarbudgetplot 関数を使用して、計算されたスキャン損失と信号処理損失が検出可能性係数に与える複合的影響を示すウォーターフォールチャートを作成します。

D = [D0 -Gi Lf Lmti_a+Lmti_b Lbint Lcfar Larray Lb];
radarbudgetplot(D, {'Single-pulse steady target','Pulse integration gain','Fluctuation loss'...
    'MTI loss', 'Binary integration loss', 'CFAR loss', 'Scan sector loss', 'Beam shape loss'});
title('Detectability Factor')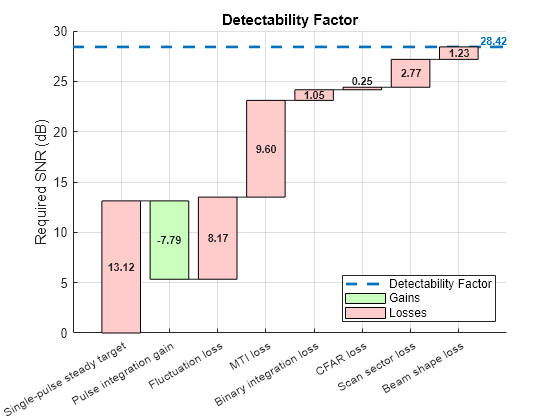

Figure contains an axes object. The axes object with title Detectability Factor, ylabel Required SNR (dB) contains 25 objects of type line, patch, text. These objects represent Detectability Factor, Losses, Gains.

結果として得られる有効検出可能性係数は 28.42 dB になります。スキャンおよび信号処理の損失を考慮すると、必要な SNR は約 15 dB 増加します。解析により、システムは実際には、 $P_{d}$ = 0.9 および $P_{f a}$ = 1e-6 で 100 km の距離にある 1 m $^{2}$ RCS ターゲットを検出するという規定の要件を満たすことができないことが示されました。

radarmetricplot(R*1e-3,SNR,sum(D), ...
    'MetricName','Available SNR', ...
    'RequirementName','Detectability', ...
    'MaxRangeRequirement',Rm*1e-3, ...
    'RangeUnit','km','MetricUnit','dB', ...
    'ShowStoplight',true, ...
    'RadarName',{'Surveillance Radar'});
title([{'Available SNR vs Range'}, {'(With STC, Eclipsing, Scanning and Signal Processing Losses)'}])
legend('Location','best')
ylim([-10 30]);

Figure contains an axes object. The axes object with title Available SNR vs Range (With STC, Eclipsing, Scanning and Signal Processing Losses), xlabel Target Range (km), ylabel Available SNR (dB) contains 6 objects of type patch, line, constantline. These objects represent Pass, Fail, Surveillance Radar, Detectability, Max Range.

この問題は、利用可能な SNR を増やすか、必要な SNR を減らすことで解決できます。より多くの電力を送信するか、アンテナゲインを増やすと、利用可能な SNR が上がり、統合時間を長くすると、必要な SNR は下がります。ただし、一部の用途では、システムパラメーターのサブセットが他の要件によって制約される場合があり、変更できないことがあります。たとえば、既存のシステムに対して解析を実行する場合、利用可能な SNR を増やすことが選択肢にならないこともあります。その場合、信号処理チェーンを調整して検出可能性係数を下げることが、許容できる解決策となり得ます。必要な SNR を下げるために、次のセクションでは、パルス数 $N$ が 10 から 40 に増加すると仮定します。

さらに、最大レンジと検出確率に関する要件を変更することもできます。目的の検出確率や最大レンジを単一の数値で指定する代わりに、Objective と Threshold の値のペアを定義できます。Objective 要件は、ミッションのニーズを完全に満たすために必要なシステムの目標パフォーマンスレベルを記述します。Threshold 要件は、システムの許容可能な最小パフォーマンスレベルを記述します。単一の値ではなく値のペアを使用して要件を定義することで、設計の柔軟性が向上し、システムパラメーターを選択するためのトレードオフの余地が生まれます。この例では、 $P_{d}$ の Objective 要件が 0.9 であると仮定し、Threshold の値を 0.8 に設定します。同様に、Objective 最大レンジ要件は 100 km のままとし、Threshold の値は 90 km に設定します。これで、検出可能性係数が、 $P_{d}$ の Objective と Threshold 両方に対して計算されるようになります。

N = 40;
M = 18;
Pd = [0.9 0.8];

[Lmti_a, Lmti_b] = mtiloss(Pd,Pfa,N,m,'Swerling1');
Dx = detectability(Pd,Pfa,N,'Swerling1') + cfarloss(Pfa,Nrc) + beamloss ...
    + Lmti_a + Lmti_b + binaryintloss(Pd,Pfa,N,M) + arrayscanloss(Pd,Pfa,N,theta,'Swerling1')

Rm = [100e3 90e3];
radarmetricplot(R*1e-3,SNR,Dx(1),Dx(2), ...
    'MetricName','Available SNR', ...
    'RequirementName','Detectability', ...
    'MaxRangeRequirement',Rm*1e-3, ...
    'RangeUnit','km','MetricUnit','dB', ...
    'ShowStoplight',true, ...
    'RadarName',{'Surveillance Radar'});
title([{'Available SNR vs Range'}, {'(N=40)'}])
legend('Location','best')
ylim([-10 30]);

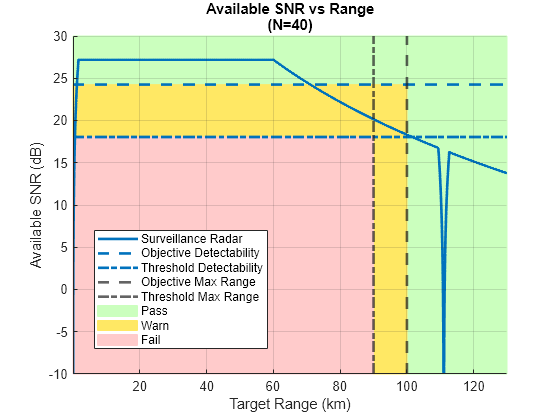
Figure contains an axes object. The axes object with title Available SNR vs Range (N=40), xlabel Target Range (km), ylabel Available SNR (dB) contains 9 objects of type patch, line, constantline. These objects represent Pass, Warn, Fail, Surveillance Radar, Threshold Detectability, Objective Detectability, Objective Max Range, Threshold Max Range.

SNR 対レンジのプロットには、システムのパフォーマンスが Objective 要件と Threshold 要件の間にある SNR 値とターゲットレンジを示す黄色の警告ゾーンが追加されました。約 70 km までは、システムが $P_{d}$ の Objective 要件を満たしていることがわかります。70 km ～ 100 km では、 $P_{d}$ の Objective 要件は違反となるものの、Threshold 要件は依然として満たされています。

有効検出確率

上記の SNR 対レンジのプロットは、レーダーシステムの検出性能がレンジによって変化することを示しています。70 km 未満のレンジにある 1 m $^{2}$ ターゲットについては、0.9 以上の検出確率で検出され、70 km ～ 100 km の間では少なくとも 0.8 の $P_{d}$ で検出されます。考慮される損失の一部は検出確率に依存するため、検出器出力における実際の $P_{d}$ はレンジによって異なります。ROC 曲線を使用することで、 $P_{d}$ をレンジの関数として計算できます。

% Generate a vector of probability values at which to compute the ROC curve
p = probgrid(0.1,0.9999,100);

% Compute the required SNR at these probabilities
[lmti_a, lmti_b] = mtiloss(p,Pfa,N,m,'Swerling1');
dx = detectability(p,Pfa,N,'Swerling1') + cfarloss(Pfa,Nrc) + beamloss ...
    + lmti_a + lmti_b + binaryintloss(p,Pfa,N,M) + arrayscanloss(p,Pfa,N,theta,'Swerling1');

% Plot the ROC curve
helperRadarPdVsSNRPlot(dx,p,[0.1 0.9999]);

Figure contains an axes object. The axes object with xlabel Effective Detectability Factor (dB), ylabel Probability of Detection contains an object of type line.

利用可能な SNR 値でこの ROC 曲線を内挿することで、検出器出力での検出の有効確率を計算できるようになりました。

% Interpolate the ROC curve at the available SNR
Pdeff = rocinterp(dx,p,SNR,'snr-pd');

% Plot the effective Pd as a function of range
radarmetricplot(R*1e-3,Pdeff,Pd(1),Pd(2), ...
    'MetricName','Effective P_d', ...
    'RequirementName','P_d', ...
    'MaxRangeRequirement',Rm*1e-3, ...
    'RangeUnit','km', ...
    'ShowStoplight',true, ...
    'RadarName',{'Surveillance Radar'});
legend('Location','best')
ylim([0.5 1.0])

Figure contains an axes object. The axes object with title Effective P_d vs Range Effective P_d vs Range, xlabel Target Range (km), ylabel Effective P indexOf d baseline Effective P_d contains 9 objects of type patch, line, constantline. These objects represent Pass, Warn, Fail, Surveillance Radar, Threshold P_d, Objective P_d, Objective Max Range, Threshold Max Range.

この結果は、STC を適用した場合、検出確率が 2 km ～ 60 km のレンジでほぼ一定であることを示しています。1 m $^{2}$ RCS のターゲットの場合、0.92 より高くなります。70 km ～ 87 km のレンジでは、有効な $P_{d}$ は 0.85 を超えます。最大レンジ要件の Threshold 値における検出確率は約 0.84 であり、Objective レンジ 100 km では 0.8 をわずかに上回ります。

まとめ

この例では、さまざまな損失がレーダーシステムの検出パフォーマンスにどのように影響するかを示します。まずレーダー方程式から始めて、利用可能な SNR と検出可能性係数の概念を紹介します。監視レーダーシステムの例を検討すると、利用可能な SNR が STC とエクリプスによってどのように減少し、一方で検出可能性係数がスキャンと信号処理の損失によってどのように増加するかがわかります。最後に、この例では、さまざまなターゲットレンジに対して受信機出力での有効検出確率を計算する方法を示します。

参考文献

Barton, D. K. Radar equations for modern radar. Artech House, 2013.
Richards, M. A., Scheer, J. A. & Holm, W. A. Principle of Modern Radar: Basic Principles. SciTech Publishing, 2010.