Current Density Between Two Metallic Conductors
This example shows how to find the electric potential and the components of the current density between two circular metallic conductors. Two metallic conductors are placed on a brine-soaked blotting paper that serves as a plane, thin conductor. The physical model for this problem is DC conduction. The boundary conditions are:
The electric potential V = 1 on the left circular conductor
The electric potential V = –1 on the right circular conductor
No surface current on the outer boundaries of the plane conductor
First, create a geometry consisting of a rectangle and two circles. Start by defining a rectangle and two circles.
R1 = [3;4
-1.2;-1.2;1.2;1.2
-0.6;0.6;0.6;-0.6];
C1 = [1;-0.6;0;0.3];
C2 = [1;0.6;0;0.3];Append extra zeros to the circles so they have the same number of rows as the rectangle.
C1 = [C1;zeros(length(R1) - length(C1),1)]; C2 = [C2;zeros(length(R1) - length(C2),1)];
Combine the shapes into one matrix.
gd = [R1,C1,C2];
Create names for the rectangle and the circles, and specify the formula to create the geometry.
ns = char('R1','C1','C2'); ns = ns'; sf = 'R1 - (C1 + C2)'; g = decsg(gd,sf,ns);
Plot the geometry with edge labels.
pdegplot(g,EdgeLabels="on")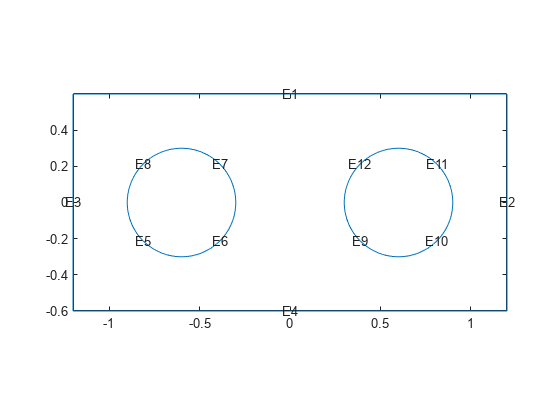
Create an femodel object for DC conduction analysis and include the geometry in the model.
model = femodel(AnalysisType="dcConduction", ... Geometry=g);
Specify the conductivity of the material as σ = 1.
model.MaterialProperties = ...
materialProperties(ElectricalConductivity=1);Specify the electric potential values on the left and right circular conductors.
model.EdgeBC(5:8) = edgeBC(Voltage=1); model.EdgeBC(9:12) = edgeBC(Voltage=-1);
Specify the zero surface current density on the outer boundaries.
model.EdgeLoad(1:4) = edgeLoad(SurfaceCurrentDensity=0);
Generate the mesh.
model = generateMesh(model);
Solve the model.
R = solve(model)
R =
ConductionResults with properties:
ElectricPotential: [1021×1 double]
ElectricField: [1×1 FEStruct]
CurrentDensity: [1×1 FEStruct]
Mesh: [1×1 FEMesh]
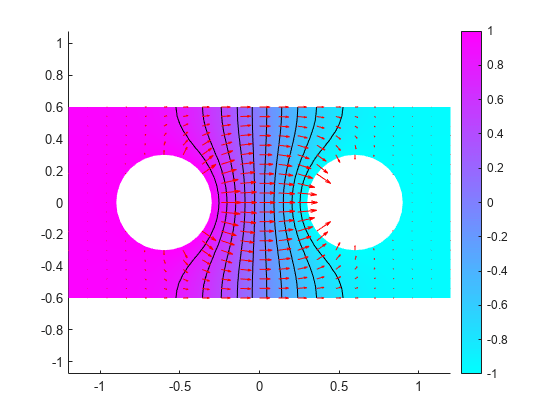
Plot the resulting electric potential and current density, and display the equipotential lines. The current flows from the conductor with a positive potential to the conductor with a negative potential. The conductivity σ is isotropic, and the equipotential lines are orthogonal to the current lines.
pdeplot(R.Mesh,XYData=R.ElectricPotential, ... Contour="on", ... FlowData=[R.CurrentDensity.Jx,R.CurrentDensity.Jy]) axis equal