並列計算手法の試行

R2025a 以降

この例では、並列計算を使用して MATLAB® コードを高速化する方法を説明します。この例を試して、MATLAB で並列計算の使用を開始する方法を確認してください。

このグラフは、この例で使用するアルゴリズムを実行した場合に、逐次計算と比較して 3 つの並列計算手法の実行にかかる時間を示しています。実際の結果は、ハードウェアによって異なります。

アルゴリズムの開発

アルゴリズムのプロトタイプを作成することから始めます。この例では、computePi 関数を使用して、$\pi$ の値を推定するモンテカルロ アルゴリズムを実行します。

このアルゴリズムは以下のステップを実行します。

1. 範囲 [0,1] で、$\mathit{m}$ 組の $\mathit{x}$ 座標と $\mathit{y}$ 座標をランダムに生成します。

2. この座標が単位正方形に内接する円内の点を表すかどうかを判定します。

3. ステップ 1 と 2 を $\mathit{n}$ 回繰り返します。

4. 円内の点の数と点の総数を使用して、$\pi$ の推定値を計算します。

モンテカルロ アルゴリズムを使用した $\pi$ の推定の詳細については、Simple Monte Carlo Area Method セクションを参照してください。

モンテカルロ アルゴリズムを作成します。

function piEst = computePi(m,n)
pointsInCircle = 0;

for i = 1:n
    % Generate random points.
    x = rand(m,1);
    y = rand(m,1);

    % Determine whether the points lie inside the unit circle.
    r = x.^2 + y.^2;
    pointsInCircle = pointsInCircle + sum(r<=1);
end

piEst = 4/(m*n) * pointsInCircle;
end

アルゴリズムによって妥当な推定値が計算されているかどうかを確認します。

m  = 3e5;
n  = 1e3;

piEst = computePi(m,n)

piEst = 
3.1415

timeit 関数を使用して、computePi 関数の実行に必要な時間を測定します。

timeSerial = timeit(@() computePi(m,n))

timeSerial = 
5.4936

並列処理手法の試用

このアルゴリズムは、並列処理を使用して高速化できます。このセクションでは、コードにわずかな変更を加えて、3 つの並列計算手法を使用してコードを実行します。次に、どの並列処理手法がこのアルゴリズムの高速化に最も適しているかを評価します。

parfor 手法

アルゴリズムに for ループが含まれ、反復順序が重要でない場合、for ループを parfor ループに変換することが通常、コードを並列化する最も簡単な方法です。

computePiParfor という新しい関数を定義します。この関数は for ループの代わりに parfor ループを使用して $\pi$ を推定します。

function piEst = computePiParfor(m,n)
pontsInCircle = 0;

parfor i = 1:n
    % Generate random points.
    x = rand(m,1);
    y = rand(m,1);

    % Determine whether the points lie inside the unit circle.
    r = x.^2 + y.^2;
    pontsInCircle = pontsInCircle + sum(r<=1);
end

piEst = 4/(m*n) * pontsInCircle;
end

スレッド ベースの並列プールを起動します。既定では、MATLAB はローカル マシン上の物理コアごとに 1 つのワーカーをもつプールを起動します。

pool = parpool("Threads");

Starting parallel pool (parpool) using the 'Threads' profile ...
Connected to parallel pool with 6 workers.

computePiParfor 関数の実行に必要な時間を測定します。

timeParfor = timeit(@() computePiParfor(m,n))

timeParfor = 
1.0548

parfor ループを使用すると、コードの変更を最小限に抑えつつ、アルゴリズムを大幅に高速化できます。

parfeval 手法

parfeval を使用して、並列ワーカー上で関数を実行できます。

calculatePoints という関数を定義します。この関数は、$\mathit{m}$ 個のランダムな点を生成し、それらの点が単位円内にあるかどうかを判定します。この関数は、元の computePi 関数で for ループの 1 回の反復に相当します。

function pointsInCircle = calculatePoints(m)
% Generate random points.
x = rand(m,1);
y = rand(m,1);

% Determine whether the points lie inside the unit circle.
r = x.^2 + y.^2;
pointsInCircle = sum(r<=1);
end

computePiParfeval という関数を定義します。この関数は parfeval を使用して $\pi$ を推定します。この関数は、for ループ内で parfeval を呼び出し、並列プール内のワーカーで calculatePoints 関数を $\mathit{n}$ 回実行します。次に、この関数は結果を使用して $\pi$ の推定値を生成します。各ワーカーには独立した乱数ストリームがあり、rand を呼び出すと各ワーカーで固有の乱数列が生成されます。ワーカー上での乱数発生の制御に関する詳細については、ワーカー上の乱数ストリームの制御を参照してください。

function piEst = computePiParfeval(m,n)

for i = 1:n
    f(i) = parfeval(@calculatePoints,1,m);
end

output  = fetchOutputs(f);
piEst = 4/(m*n) * sum(output);
end

computePiParfeval 関数の実行に必要な時間を測定します。

timeParfeval = timeit(@() computePiParfeval(m,n))

timeParfeval = 
1.3845

実行時間からわかるように、parfeval は現在の形で用いるのであれば、この問題には適していません。calculatePoints 関数が極めて短時間で実行されるため、通信およびスケジューリングのオーバーヘッドが大きくなるからです。ただし、parfeval は、望ましい結果が既知である一方、その結果を得るまでに必要な反復回数が不明な問題には適しています。たとえば、$\pi$ の推定値を解が改善しなくなるまで反復的に改良する場合、parfeval を使用して 10,000 回分の反復をキューに入れ、目標に達した時点で、残りの反復をすべてキャンセルすることもできます。parfeval を使用して$\pi$ を計算する改良版の関数 computePiParfevalImproved がサポート ファイルとして、この例に添付されています。このサポート ファイルにアクセスするには、この例をライブ スクリプトとして開きます。

GPU 手法

サポートされている GPU がある場合、GPU 上でコードを実行することで、コードを高速化できます。サポートされている GPU の詳細については、GPU 計算の要件を参照してください。

gpu = gpuDevice;
disp(gpu.Name + " GPU selected.")

NVIDIA RTX A5000 GPU selected.

computePiGPU という新しい関数を定義します。この関数は、GPU 上で $\pi$ を推定します。MATLAB および他のツールボックスの関数の多くは、gpuArray データ引数を指定すると、自動的に GPU で実行されます。computePiGPU 関数はランダムな点を gpuArray データとして生成し、その後の計算は自動的に GPU で実行されます。

function piEst = computePiGPU(m,n)
c = zeros(1,"gpuArray");

for i = 1:n
    % Generate random points on the GPU.
    x = rand(m,1,"gpuArray");
    y = rand(m,1,"gpuArray");

    % Determine whether the points lie inside the unit circle.
    r = x.^2 + y.^2;
    c = c + sum(r<=1);
end

piEst = 4/(m*n) * c;
end

gputimeit 関数を使用して、computePiGPU 関数の実行に必要な時間を測定します。GPU を使用する関数については、gputimeit 関数の方が timeit よりも推奨されます。GPU でのすべての演算が完了してから時間が記録されるためです。これにより、オーバーヘッドが補正されます。

timeGPU = gputimeit(@() computePiGPU(m,n))

timeGPU = 
0.2079

for ループをベクトル化することで、このコードを GPU 上でさらに高速化できます。ベクトル化は、ループベースのコードを MATLAB の行列演算およびベクトル演算を使用するように変更するプロセスです。GPU は一般に、多数の演算を実行する場合に効果を発揮します。したがって、コードのベクトル化は、GPU で実行される高速化されたコードに特に有効です。ベクトル化コードを使用して GPU で $\pi$ を計算する改良版の関数 computePiGPUVectorized がサポート ファイルとして、この例に添付されています。このサポート ファイルにアクセスするには、この例をライブ スクリプトとして開きます。

実行時間の比較

並列手法の実行時間を逐次実行の場合と比較します。

figure
bar([timeSerial timeParfor timeParfeval timeGPU])
xlabel("Execution Type")
xticklabels(["Serial" "Parfor" "Parfeval" "GPU"])
ylabel("Execution Time (s)")
grid on

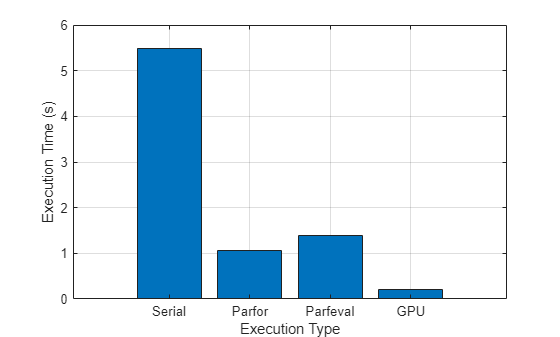
この例で使用するアルゴリズムを実行した場合、3 つの並列計算手法の実行時間は、逐次計算と比較して大幅に高速です。実際の結果は、ハードウェアによって異なります。

シンプルなモンテカルロ面積法

半径 $\mathit{r}$ の円が各辺の長さ $2\mathit{r}$ の正方形に内接している場合、円の面積と正方形の面積の関係が $\pi$ で与えられます。次の図は、この問題を示したものです。

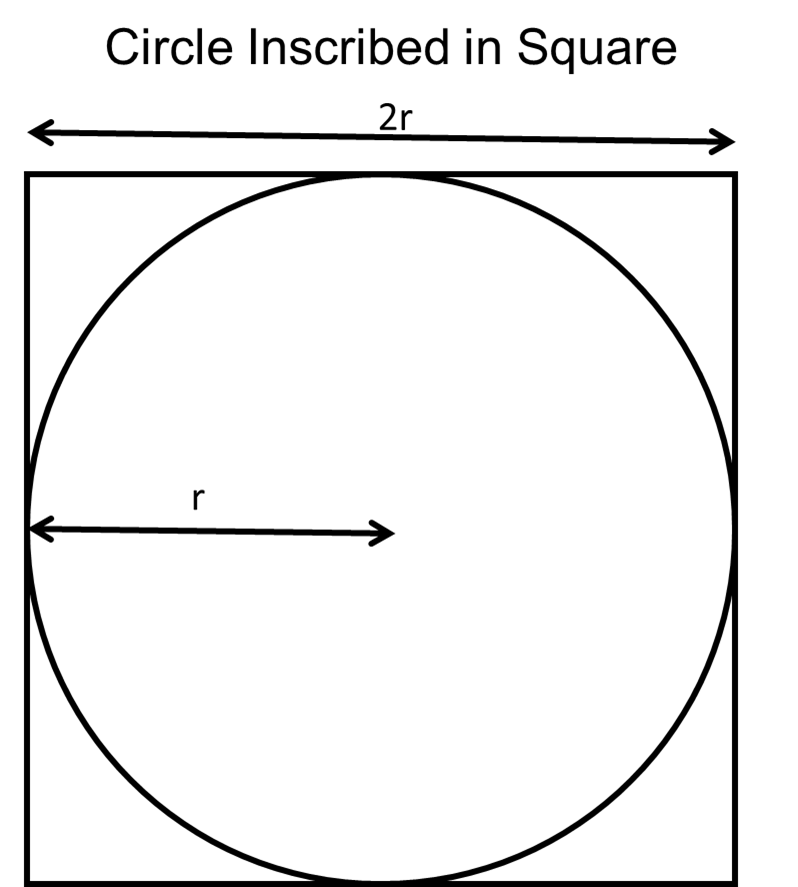
円の面積を正方形の面積で除算した比から $\pi$ を導出できます。

$\frac{\mathrm{area}\mathrm{of}\mathrm{circle}}{\mathrm{area}\mathrm{of}\mathrm{square}}=$

$\frac{\pi {\mathit{r}}^2}{{\left(2\mathit{r}\right)}^2}=\frac{\pi }{4}$

$\pi$ を直接使用せずに円の面積を推定するには、正方形の中に点の一様なサンプルをランダムに生成し、円の内側にある点の数をカウントします。点が円の内側にある確率は、円の面積を正方形の面積で除算した比になります。

点が円の内側にあるかどうかを判定するには、点の $\mathit{x}$ 座標と $\mathit{y}$ 座標の 2 つの値をランダムに生成し、点から円の原点までの距離を計算します。原点から生成された点までの距離 $\mathit{d}$ は、次の方程式で与えられます。

$$\mathit{d}=\sqrt{{\mathit{x}}^2+{\mathit{y}}^2}$$

$\mathit{d}$ が円の半径 $\mathit{r}$ よりも小さければ、点は円の内側にあります。大規模な点のサンプルを生成し、円の内側にある数をカウントします。このデータを使用して、円の内側にある点と生成された点の総数の比を取得します。この比は、円の面積と正方形の面積の比と等価です。これにより、以下を使用して $\pi$ を推定できます。

$\frac{\mathrm{points}\mathrm{in}\mathrm{circle}}{\mathrm{total}\mathrm{number}\mathrm{of}\mathrm{points}}\approx \frac{\pi }{4}$

$$\pi \approx 4\times \frac{\mathrm{points}\mathrm{in}\mathrm{circle}}{\mathrm{total}\mathrm{number}\mathrm{of}\mathrm{points}}$$

参考

parfor | parfeval | gpuArray

トピック

• 並列計算の解決策の選択
• 並列言語の意思決定表