メッセージ パッシングを使った π の数値推定
この例では spmd ステートメント取り扱いの基本と、それがどのような形で並列計算実行の対話型手段となるのかを示します。これを行うために、π を近似する比較的単純な計算を実行します。
この例のコードは以下の関数に含まれています。
function paralleldemo_quadpi_mpi
はじめに
ここでは以下の事実を利用します。
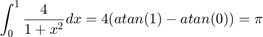
左辺の積分を近似することで、π の近似値を求めます。
並列プールで並列計算を実行し、spmd キーワードを使用してコードの並列ブロックをマークします。最初に、現在開いている並列プールのサイズを確認します。
p = gcp; p.NumWorkers
Starting parallel pool (parpool) using the 'Processes' profile ...
Connected to the parallel pool (number of workers: 6).
ans =
6
計算の並列化
4/(1 + x^2) を 0 から 1 まで数値積分して、π を近似します。
type pctdemo_aux_quadpi.m
function y = pctdemo_aux_quadpi(x) %PCTDEMO_AUX_QUADPI Return data to approximate pi. % Helper function used to approximate pi. This is the derivative % of 4*atan(x). % Copyright 2008 The MathWorks, Inc. y = 4./(1 + x.^2);
図中に示すような [0, 1] の部分区間に対し関数の積分を各ワーカーに計算させることにより、作業をワーカー間で分割します。
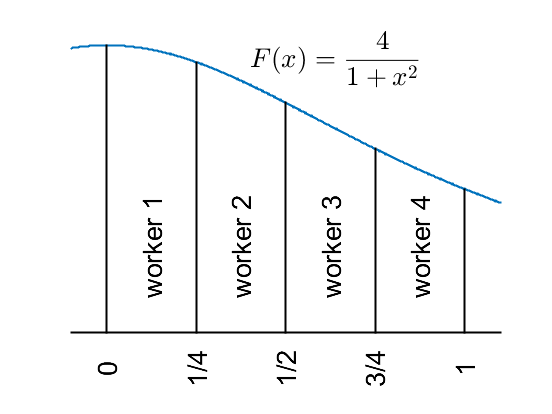
変数 a および b をすべてのワーカーで定義しますが、区間 [a, b] が図に示された部分区間に対応するように、それらの値が spmdIndex に応じて決まるようにします。そのうえで、区間が適正であることを確認します。spmd ステートメント本文のコードは、並列プールのすべてのワーカーで並列に実行されることに注意してください。
spmd a = (spmdIndex - 1)/spmdSize; b = spmdIndex/spmdSize; fprintf('Subinterval: [%-4g, %-4g]\n', a, b); end
ここで、すべてのワーカーで MATLAB 求積法を使用し、各積分の近似値を求めます。上図に示すように、いずれも同じ関数で演算が行われますが、演算対象は [0, 1] の異なる部分区間となります。
spmd myIntegral = integral(@pctdemo_aux_quadpi, a, b); fprintf('Subinterval: [%-4g, %-4g] Integral: %4g\n', ... a, b, myIntegral); end
結果の加算
ワーカーで関数の積分の担当部分をすべて計算し終わったら、結果を加算して [0, 1] 全体での積分を求めます。関数 spmdPlus を使用してすべてのワーカーの myIntegral を加算し、すべてのワーカーでの合計を返します。
spmd piApprox = spmdPlus(myIntegral); end
クライアントでの結果の検査
変数 piApprox は spmd ステートメントの内部に割り当てられたため、クライアント上で Composite としてアクセスできます。Composite オブジェクトは、1 つの要素に各ワーカーを対応させた場合の cell 配列に似ています。Composite にインデックスを付けると、対応する値がワーカーからクライアントに戻されます。
approx1 = piApprox{1}; % 1st element holds value on worker 1.
fprintf('pi : %.18f\n', pi);
fprintf('Approximation: %.18f\n', approx1);
fprintf('Error : %g\n', abs(pi - approx1))
pi : 3.141592653589793116 Approximation: 3.141592653589793116 Error : 0