発電機の最適な運転スケジュール: ソルバーベース

ライブスクリプトを開く

この例では、収益からコストを引いた後の利益を最大化するよう、2 台のガス火力発電機の最適な運転スケジュールを設定する方法を示します。必ずしも現実的な例ではありませんが、判定のタイミングに応じて変動するコストを考慮する方法が説明されています。

この問題への問題ベースのアプローチについては、発電機の最適な運転スケジュール: 問題ベースを参照してください。

問題の定義

電力市場の価格は、一日の間にその時間帯によって変動します。発電機を運転する場合、価格が高い時間帯に稼働するようスケジュールを設定することで、この価格の変動を有利に利用することができます。たとえば、2 台の発電機を管理していると仮定します。各発電機にオフ、低、高の 3 つの稼働レベルがあり、そのレベルごとに各発電機の燃料消費と電力生産量が決まっています。当然ながら、発電機がオフのときの燃料消費量は 0 になります。

1 日につき 30 分ごとの間隔 (つまり 24 時間に 48 回) で、各発電機に稼働レベルを割り当てることができます。過去の記録から、この各時間枠におけるメガワット時 (MWh) あたりの収益がわかっているとします。この例のデータは Australian Energy Market Operator 提供による https://www.nemweb.com.au/REPORTS/CURRENT/ 2013 年中期レポートから引用したもので、同社の利用条件 https://www.aemo.com.au/privacy-and-legal-notices/copyright-permissions のもとに使用されています。

load dispatchPrice; % Get poolPrice, which is the revenue per MWh
bar(poolPrice,.5)
xlim([.5,48.5])
xlabel('Price per MWh at each period')

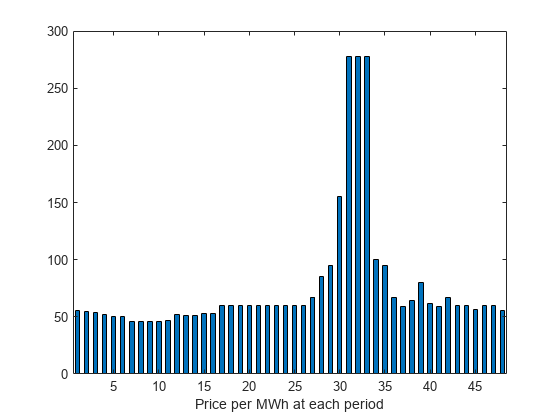
発電機をいったんオフにした後で運転を再開するには、コストがかかります。さらに、一日の最大燃料消費量の制約も適用されます。最大燃料消費量の制約があるのは、燃料は前日に購入し、購入しただけの分しか使用できないためです。

問題の表記とパラメーター

このスケジュール設定問題は、次のように 0-1 整数計画問題として定式化できます。インデックス i、j および k と、2 値のスケジュール設定ベクトル y を、次のように定義します。

nPeriods = 期間数 (ここでは 48)。
i = 1 期間、1 <= i <= 48。
j = 発電機インデックス、ここでは 1 <= j <= 2。
期間 i に発電機 j がレベル k で稼働している場合、y(i,j,k) = 1 となります。ここで低稼働レベルを k = 1 とし、高稼働レベルを k = 2 とします。sum_k y(i,j,k) = 0 の場合、発電機はオフになっています。

オフにした発電機については、運転をいつ再開するかを判断する必要があります。次のように仮定します。

発電機 j が期間 i にオフで、期間 i + 1 にオンの場合は z(i,j) = 1。それ以外の場合は z(i,j) = 0。言い換えれば、sum_k y(i,j,k) = 0 かつ sum_k y(i+1,j,k) = 1 のときに z(i,j) = 1 となります。

ここで当然ながら、y の設定に基づいて z を自動的に設定する方法が必要になります。この設定は、次の線形制約によって処理します。

上記のほかに、コスト、各発電機の電力生産レベル、消費レベルおよび使用できる燃料を表すパラメーターも必要です。

poolPrice(i) -- 期間 i における MWh あたりの収益 (ドル単位)。
gen(j,k) -- 発電機 j によって稼働レベル k で生産される MW 数。
fuel(j,k) -- 発電機 j によって稼働レベル k で消費される燃料。
totalfuel -- 1 日に使用できる燃料。
startCost -- いったんオフにした発電機を再稼働させるためのコスト (ドル単位)。
fuelPrice -- 燃料の単位あたりコスト。

poolPrice は load dispatchPrice; の実行時に計算済みです。その他のパラメーターは次のように設定します。

fuelPrice = 3;
totalfuel = 3.95e4;
nPeriods = length(poolPrice); % 48 periods
nGens = 2; % Two generators
gen = [61,152;50,150]; % Generator 1 low = 61 MW, high = 152 MW
fuel = [427,806;325,765]; % Fuel consumption for generator 2 is low = 325, high = 765
startCost = 1e4; % Cost to start a generator after it has been off

発電機の効率性

2 つの稼働点における、2 台の発電機の効率性を調べます。

efficiency = gen./fuel; % Calculate electricity per unit fuel use
rr = efficiency'; % for plotting
h = bar(rr);
h(1).FaceColor = 'g';
h(2).FaceColor = 'c';
legend(h,'Generator 1','Generator 2','Location','NorthEastOutside')
ax = gca;
ax.XTick = [1,2];
ax.XTickLabel = {'Low','High'};
ylim([.1,.2])
ylabel('Efficiency')

ここで、それぞれ対応する稼働点 (低または高) においては発電機 2 の方が発電機 1 よりも若干効率が高くなっていますが、高稼働点における発電機 1 は、低稼働点における発電機 2 よりも効率が良いことに注意してください。

解の変数

問題を設定するには、すべての問題データと制約を、intlinprog ソルバーが要求する形式にエンコードする必要があります。問題の解を表す変数 y(i,j,k) と、発電機の運転開始にかかるコストを表す補助変数 z(i,j) を使用します。ここで、y は nPeriods-by-nGens-by-2 の配列、z は nPeriods-by-nGens の配列です。

これらの変数を 1 つの長いベクトルに配置するには、不明値の変数 x を次のように定義します。

x = [y(:);z(:)];

範囲制約と線形制約には、y と z の自然な配列数式を使用して、これらの制約を総合決定変数のベクトル x に変換するのが一番簡単な方法です。

範囲

解のベクトル x は、2 値変数で構成されます。lb と ub の範囲を設定します。

lby = zeros(nPeriods,nGens,2); % 0 for the y variables
lbz = zeros(nPeriods,nGens); % 0 for the z variables
lb = [lby(:);lbz(:)]; % Column vector lower bound
ub = ones(size(lb)); % Binary variables have lower bound 0, upper bound 1

線形制約

線形制約 A*x <= b では、行列 A の列数が x の長さと同じでなければなりません。これは、lb の長さと同じです。A の行を適切なサイズで作成するには、行列 y と行列 z のサイズをもつゼロ行列をそれぞれ作成します。

cleary = zeros(nPeriods,nGens,2);
clearz = zeros(nPeriods,nGens);

稼働レベルに、1 に等しい成分が複数指定されないよう、次の線形不等式制約を設定します。

x(i,j,1) + x(i,j,2) <= 1

A = spalloc(nPeriods*nGens,length(lb),2*nPeriods*nGens); % nPeriods*nGens inequalities
counter = 1;
for ii = 1:nPeriods
    for jj = 1:nGens
        temp = cleary;
        temp(ii,jj,:) = 1;
        addrow = [temp(:);clearz(:)]';
        A(counter,:) = sparse(addrow);
        counter = counter + 1;
    end
end
b = ones(nPeriods*nGens,1); % A*x <= b means no more than one of x(i,j,1) and x(i,j,2) are equal to 1

1 期間あたりの運転費が、その期間の燃料コストです。発電機 j がレベル k で稼働している場合、コストは fuelPrice * fuel(j,k) となります。

発電機による燃料の過剰消費を避けるには、総燃料消費量に対する不等式制約を作成します。

yFuel = lby; % Initialize fuel usage array
yFuel(:,1,1) = fuel(1,1); % Fuel use of generator 1 in low setting
yFuel(:,1,2) = fuel(1,2); % Fuel use of generator 1 in high setting
yFuel(:,2,1) = fuel(2,1); % Fuel use of generator 2 in low setting
yFuel(:,2,2) = fuel(2,2); % Fuel use of generator 2 in high setting

addrow = [yFuel(:);clearz(:)]';
A = [A;sparse(addrow)];
b = [b;totalfuel]; % A*x <= b means the total fuel usage is <= totalfuel

発電機の稼働開始指標変数の設定

y 変数で表されるオンとオフの期間に応じてソルバーが z 変数を自動的に設定できるようにするには、次のようにします。ここで、条件 z(i,j) = 1 が

厳密に sum_k y(i,j,k) = 0 かつ sum_k y(i+1,j,k) = 1 という条件下において満たされる必要がある点に注意します。

つまり、

z(i,j) = 1 が厳密に満たされる場合に、sum_k ( - y(i,j,k) + y(i+1,j,k) ) > 0 となります。

したがって、問題の定式化に次の線形不等式制約

sum_k ( - y(i,j,k) + y(i+1,j,k) ) - z(i,j) < = 0

を含め、目的関数のコストに z 変数を含めます。変数 z を目的関数に含めることで、ソルバーが変数 z の値を低くしようとします。つまり、ソルバーはすべての値を 0 に等しく設定しようとします。しかし、発電機がオンになっている期間では、線形不等式によって z(i,j) が 1 に等しくなるよう強制されます。

これらの新しい不等式を表すには、線形不等式制約行列 A に行を追加します。時刻をラップさせて期間 48 の後に期間 1 が来るように調整します。

tempA = spalloc(nPeriods*nGens,length(lb),2*nPeriods*nGens);
counter = 1;
for ii = 1:nPeriods
    for jj = 1:nGens
        temp = cleary;
        tempy = clearz;
        temp(ii,jj,1) = -1;
        temp(ii,jj,2) = -1;
        if ii < nPeriods % Intervals 1 to 47
            temp(ii+1,jj,1) = 1;
            temp(ii+1,jj,2) = 1;
        else % Interval 1 follows interval 48
            temp(1,jj,1) = 1;
            temp(1,jj,2) = 1;
        end
        tempy(ii,jj) = -1;
        temp = [temp(:);tempy(:)]'; % Row vector for inclusion in tempA matrix
        tempA(counter,:) = sparse(temp);
        counter = counter + 1;
    end
end
A = [A;tempA];
b = [b;zeros(nPeriods*nGens,1)]; % A*x <= b sets z(i,j) = 1 at generator startup

制約のスパース性

大規模問題の場合はスパース制約行列を使用すると、メモリを節約して計算時間を短縮できます。制約行列 A は非常にスパースです。

filledfraction = nnz(A)/numel(A)

filledfraction = 0.0155

intlinprog はスパースな線形制約行列 A と Aeq を受け入れますが、それぞれ対応するベクトル制約 b と beq には非スパース行列を必要とします。

目的の定義

目的関数には、発電機の運転時の燃料コスト、発電機の運転から得られる収益および発電機を運転開始するためのコストが含まれます。

generatorlevel = lby; % Generation in MW, start with 0s
generatorlevel(:,1,1) = gen(1,1); % Fill in the levels
generatorlevel(:,1,2) = gen(1,2);
generatorlevel(:,2,1) = gen(2,1);
generatorlevel(:,2,2) = gen(2,2);

収益 = x.*generatorlevel.*poolPrice

revenue = generatorlevel; % Allocate revenue array
for ii = 1:nPeriods
    revenue(ii,:,:) = poolPrice(ii)*generatorlevel(ii,:,:);
end

合計燃料コスト= y.*yFuel*fuelPrice

fuelCost = yFuel*fuelPrice;

運転開始コスト= z.*ones(size(z))*startCost

starts = (clearz + 1)*startCost;
starts = starts(:); % Generator startup cost vector

ベクトル x = [y(:);z(:)]。収益合計を x で記述します。

利益 = 収益 - 合計燃料コスト - 運転開始コスト

f = [revenue(:) - fuelCost(:);-starts]; % f is the objective function vector

問題を解く

スペースを節約するため、反復表示を抑制します。

options = optimoptions('intlinprog','Display','final');
[x,fval,eflag,output] = intlinprog(-f,1:length(f),A,b,[],[],lb,ub,options);

Optimal solution found.

Intlinprog stopped because the objective value is within a gap tolerance of the optimal value, options.RelativeGapTolerance = 0.0001. The intcon variables are integer within tolerance, options.ConstraintTolerance = 1e-06.

解の検証

解を検証する一番簡単な方法は、解のベクトル x をその 2 つの成分である y と z に分割することです。

ysolution = x(1:nPeriods*nGens*2);
zsolution = x(nPeriods*nGens*2+1:end);
ysolution = reshape(ysolution,[nPeriods,nGens,2]);
zsolution = reshape(zsolution,[nPeriods,nGens]);

解を時間の関数としてプロットします。

subplot(3,1,1)
bar(ysolution(:,1,1)*gen(1,1)+ysolution(:,1,2)*gen(1,2),.5,'g')
xlim([.5,48.5])
ylabel('MWh')
title('Generator 1 optimal schedule','FontWeight','bold')
subplot(3,1,2)
bar(ysolution(:,2,1)*gen(2,1)+ysolution(:,2,2)*gen(2,2),.5,'c')
title('Generator 2 optimal schedule','FontWeight','bold')
xlim([.5,48.5])
ylabel('MWh')
subplot(3,1,3)
bar(poolPrice,.5)
xlim([.5,48.5])
title('Energy price','FontWeight','bold')
xlabel('Period')
ylabel('$ / MWh')

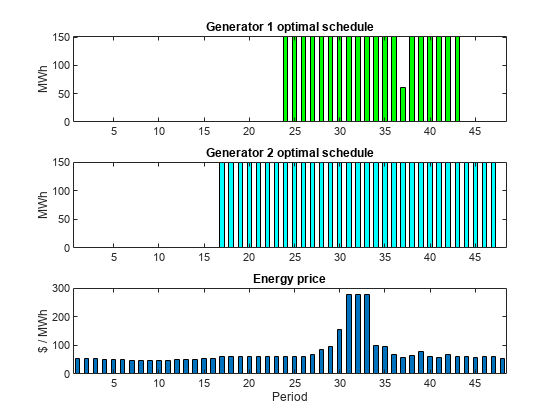
発電機 2 は発電機 1 より長い時間稼働します。これは発電機 2 の方が効率性が高いことから容易に予想できます。発電機 2 が稼働するときは、常に最高のレベルで稼働します。発電機 1 は主に高レベルで稼働しますが、1 期間に限り低レベルに落として稼働します。各発電機は毎日連続した期間にわたって稼働するため、運転開始コストが発生するのは 1 度だけです。

発電機が運転を開始する期間の z 変数が 1 であることを確認してください。

starttimes = find(round(zsolution) == 1); % Use round for noninteger results
[theperiod,thegenerator] = ind2sub(size(zsolution),starttimes)

theperiod = 2×1

    23
    16

thegenerator = 2×1

     1
     2

発電機がオンになる期間は、プロットに一致しています。

運転開始のペナルティを下げた場合との比較

startCost の値を小さくすると、解で複数の電力生産期間が使用されます。

startCost = 500; % Choose a lower penalty for starting the generators
starts = (clearz + 1)*startCost;
starts = starts(:); % Start cost vector
fnew = [revenue(:) - fuelCost(:);-starts]; % New objective function
[xnew,fvalnew,eflagnew,outputnew] = ...
    intlinprog(-fnew,1:length(fnew),A,b,[],[],lb,ub,options);

Optimal solution found.

Intlinprog stopped because the objective value is within a gap tolerance of the optimal value, options.RelativeGapTolerance = 0.0001. The intcon variables are integer within tolerance, options.ConstraintTolerance = 1e-06.

ysolutionnew = xnew(1:nPeriods*nGens*2);
zsolutionnew = xnew(nPeriods*nGens*2+1:end);
ysolutionnew = reshape(ysolutionnew,[nPeriods,nGens,2]);
zsolutionnew = reshape(zsolutionnew,[nPeriods,nGens]);

subplot(3,1,1)
bar(ysolutionnew(:,1,1)*gen(1,1)+ysolutionnew(:,1,2)*gen(1,2),.5,'g')
xlim([.5,48.5])
ylabel('MWh')
title('Generator 1 optimal schedule','FontWeight','bold')
subplot(3,1,2)
bar(ysolutionnew(:,2,1)*gen(2,1)+ysolutionnew(:,2,2)*gen(2,2),.5,'c')
title('Generator 2 optimal schedule','FontWeight','bold')
xlim([.5,48.5])
ylabel('MWh')
subplot(3,1,3)
bar(poolPrice,.5)
xlim([.5,48.5])
title('Energy price','FontWeight','bold')
xlabel('Period')
ylabel('$ / MWh')

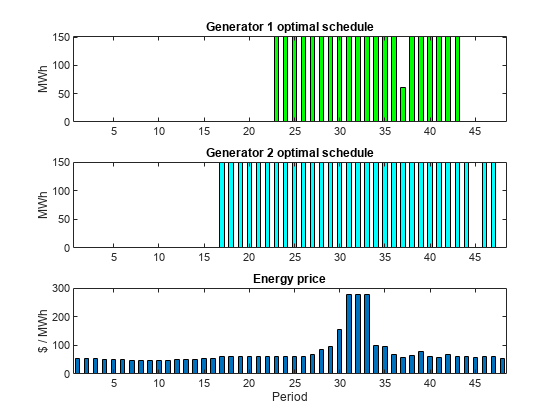
starttimes = find(round(zsolutionnew) == 1); % Use round for noninteger results
[theperiod,thegenerator] = ind2sub(size(zsolution),starttimes)

theperiod = 3×1

    22
    16
    45

thegenerator = 3×1

     1
     2
     2