0-1 整数計画法によるオフィスの割り当て: ソルバーベース

ライブスクリプトを開く

この例では、関数 intlinprog を使用して、0-1 整数計画によって割り当ての問題を解く方法を説明します。この問題への問題ベースのアプローチについては、0-1 整数計画法によるオフィスの割り当て: 問題ベースを参照してください。

オフィス割り当て問題

Marcelo、Rakesh、Peter、Tom、Marjorie および Mary Ann の 6 人を 7 つのオフィスに割り当てたいと思います。各オフィスに配置できるのは 1 人だけで、各人は正確に 1 つのオフィスにのみ割り当てられます。そのため、空きオフィスが 1 つになります。これらの人はオフィスを選ぶことができ、彼らの選好を考慮する際は年功が基準とされます。MathWorks での勤続年数が長いほど年功が高くなります。窓のあるオフィスと窓のないオフィスがあり、また、1 つの窓は他より小さくなっています。さらに、Peter と Tom はよく一緒に働いているため、隣接するオフィスに配置する必要があります。Marcelo と Rakesh もよく一緒に働いているため、隣接するオフィスに配置する必要があります。

オフィスのレイアウト

オフィス 1、2、3、および 4 は建物の内側にあり、窓がありません。オフィス 5、6 および 7 には窓がありますが、オフィス 5 の窓は他の 2 つのオフィスよりも小さいです。ここで、これらのオフィスの配置方法を示します。

name = {'Office 1','Office 2','Office 3','Office 4','Office 5','Office 6','Office 7'};
printofficeassign(name)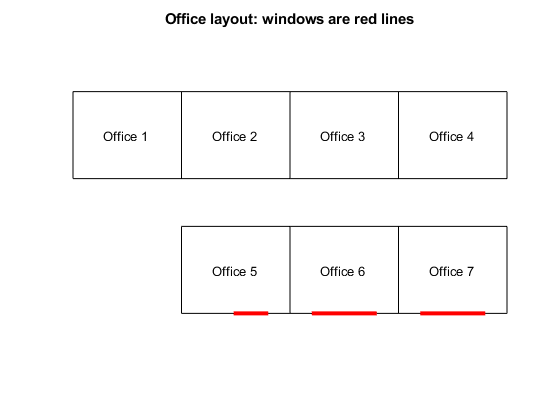

問題の定式化

この問題を数学的に定式化する必要があります。最初に、問題において解変数 x の各要素が表すものを選択します。これは 0-1 整数問題であるため、オフィスに割り当てられる人を各要素が表すようにすることが適切な選択です。社員がオフィスに割り当てられると変数の値が 1 になり、割り当てられないと 0 になります。各人に次のように番号を付けます。

Mary Ann
Marjorie
Tom
Peter
Marcelo
Rakesh

x はベクトルです。要素 x(1) ～ x(7) は、オフィス 1 ～オフィス 7 に割り当てられている Mary Ann に相当します。次の 7 つの要素は、オフィス 1 ～オフィス 7 に割り当てられている Marjorie に相当します (以下、他の人についても同様)。6 人を 7 つのオフィスに割り当てるため、x ベクトルの要素は合計で 42 個になります。

年功

MathWorks での勤続年数が長いほど選好が重視されるように、年功に基づいて選好に重みを付けたいと思います。年功は以下のようになっています。Mary Ann は 9 年、Marjorie は 10 年、Tom は 5 年、Peter は 3 年、Marcelo は 1.5 年、Rakesh は 2 年です。年功に基づいて、正規化された重みベクトルを作成します。

seniority = [9 10 5 3 1.5 2];
weightvector = seniority/sum(seniority);

人々のオフィスの好み

行がオフィスに対応し、列が人に対応するような選好行列を設定します。各社員の希望は数値で示されています。各人が各オフィスについて値を入れ、その選択の合計、つまり列の値の合計が 100 になるように依頼します。ここでは第一希望のオフィスの数値が最も大きくなります。各人の選好が列ベクトルにリストされます。

MaryAnn = [0; 0; 0; 0; 10; 40; 50];
Marjorie = [0; 0; 0; 0; 20; 40; 40];
Tom = [0; 0; 0; 0; 30; 40; 30];
Peter = [1; 3; 3; 3; 10; 40; 40];
Marcelo = [3; 4; 1; 2; 10; 40; 40];
Rakesh = [10; 10; 10; 10; 20; 20; 20];

各人の選好ベクトルの i 番目の要素は、その人物が i 番目のオフィスをどの程度評価しているかを示しています。つまり、選好行列を組み合わせたものは次のようになります。

prefmatrix = [MaryAnn Marjorie Tom Peter Marcelo Rakesh];

年功が列の基準となるように、weightvector を使用して選好行列に重みを付けます。また、この行列を列順にベクトルに変換して、x ベクトルに対応するようにすれば、より都合が良くなります。

PM = prefmatrix * diag(weightvector);
c = PM(:);

目的関数

目的は、年功によって重みが付けられた選好の満足度を最大限にすることです。以下は線形目的関数です。

max c'*x

これは、次の関数と等価です。

min -c'*x.

制約

最初の制約セットでは、各人が正確に 1 つのオフィスを得ることが求められます。つまり、各人について、該当する人に対応する x 値の合計が正確に 1 であることが求められます。たとえば、2 番目の人である Marjorie の場合、これは sum(x(8:14))=1 であることを意味します。適切な行列を作成することで、これらの線形制約を等式行列 Aeq とベクトル beq (ここで、Aeq*x = beq) で表します。行列 Aeq は、1 と 0 で構成されます。たとえば、Aeq の 2 番目の行は、1 つのオフィスを得る Marjorie に対応しており、行は以下のようになります。

0 0 0 0 0 0 0 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 ... 0 0 0

つまり、列 8 ～ 14 に 7 個の 1 があり、他の列はゼロです。Aeq(2,:)*x = 1 は、sum(x(8:14)) = 1 と等価です。

numOffices = 7;
numPeople = 6;
numDim = numOffices * numPeople;
onesvector = ones(1,numOffices);

Aeq の各行は、1 人に対応します。

Aeq = blkdiag(onesvector,onesvector,onesvector,onesvector, ...
    onesvector,onesvector);
beq = ones(numPeople,1);

第 2 の制約セットは不等式です。これらの制約では、各オフィスに 1 人だけ配置される (つまり、各オフィスに 1 人がいるか誰もいない) ように指定されます。これらの制約を表現するために、A*x <= b となるような行列 A とベクトル b を作成します。A と b の各行はオフィスに対応します。したがって、行 1 はオフィス 1 に割り当てられる社員を示します。今回、各行はこのような配列になり、行 1 は次のようになります。

1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 ... 1 0 0 0 0 0 0

この後の各行は、これと似ていますが、右に 1 つシフト (循環的に) したものになります。たとえば、行 3 はオフィス 3 に対応しており、A(3,:)*x <= 1 (つまり、オフィス 3 には 1 人しか配置できないこと) を示しています。

A = repmat(eye(numOffices),1,numPeople);
b = ones(numOffices,1);

次の制約セットも不等式であるため、それらを、上記から既に不等式を含んでいる行列 A とベクトル b に追加します。Tom と Peter には、互いに隣接したオフィスを割り当てたいと思います。Marcelo と Rakesh についても同様です。まず、彼らの物理的位置に基づき、近似マンハッタン距離を使用してオフィスの距離行列を作成します。これは対称行列です。

D = zeros(numOffices);

行列の右上半分を設定します。

D(1,2:end) = [1 2 3 2 3 4];
D(2,3:end) = [1 2 1 2 3];
D(3,4:end) = [1 2 1 2];
D(4,5:end) = [3 2 1];
D(5,6:end) = [1 2];
D(6,end)   = 1;

左下半分は右上と同じです。

D = triu(D)' + D;

距離単位が 1 距離単位を超えているオフィスを見つけます。

[officeA,officeB] = find(D > 1);
numPairs = length(officeA)

numPairs = 26

これにより、隣接していないオフィスの numPairs ペアが見つかります。これらのペアに関して、Tom がペアの一方のオフィスを占有している場合、Peter はペアの他方のオフィスを占有できません。もし占有していれば、彼らは隣接していないオフィスに配置されることになってしまいます。Marcelo と Rakesh についても該当します。これにより、さらに 2*numPairs 多い不等式制約が与えられ、これらの制約を A と b に追加することになります。

これらの制約に対応するための十分な行を A に追加します。

numrows = 2*numPairs + numOffices; 
A((numOffices+1):numrows, 1:numDim) = zeros(2*numPairs,numDim);

numPairs の各オフィスペア、officeA の Tom に対応する x(i) および OfficeB の Peter に対応する x(j) について、制約は以下のようになります。

x(i) + x(j) <= 1.

Tom または Peter のどちらかがこれらのオフィスの 1 つを占有できますが、両人とも占有することはできません。

Tom の番号は 3、Peter の番号は 4 です。

tom = 3;
peter = 4;

Marcelo の番号は 5、Rakesh の番号は 6 です。

marcelo = 5;
rakesh = 6;

以下の無名関数が、それぞれ Tom、Peter、Marcelo、Rakesh に対応するオフィス i のインデックスを返します。

tom_index=@(officenum) (tom-1)*numOffices+officenum;
peter_index=@(officenum) (peter-1)*numOffices+officenum;
marcelo_index=@(officenum) (marcelo-1)*numOffices+officenum;
rakesh_index=@(officenum) (rakesh-1)*numOffices+officenum;

for i = 1:numPairs    
    tomInOfficeA = tom_index(officeA(i));
    peterInOfficeB = peter_index(officeB(i));
    A(i+numOffices, [tomInOfficeA, peterInOfficeB]) = 1;
   
    % Repeat for Marcelo and Rakesh, adding more rows to A and b.
    marceloInOfficeA = marcelo_index(officeA(i));
    rakeshInOfficeB = rakesh_index(officeB(i));
    A(i+numPairs+numOffices, [marceloInOfficeA, rakeshInOfficeB]) = 1;
end
b(numOffices+1:numOffices+2*numPairs) = ones(2*numPairs,1);

`intlinprog` による求解

問題の定式化は、以下の線形目的関数で構成されます。

min -c'*x

従う線形制約は

Aeq*x = beq

A*x <= b

変数はすべて 2 値です。

A、b、Aeq および beq は既に入力されています。ここで、目的関数を設定します。

f = -c;

変数が 2 進数であるかどうかを確認するには、下限を 0、上限を 1 に指定し、intvars を設定してすべての変数を表します。

lb = zeros(size(f));
ub = lb + 1;
intvars = 1:length(f);

intlinprog を呼び出してこの問題を解きます。

[x,fval,exitflag,output] = intlinprog(f,intvars,A,b,Aeq,beq,lb,ub);

LP:                Optimal objective value is -33.868852.                                           

Cut Generation:    Applied 1 Gomory cut.                                                            
                   Lower bound is -33.836066.                                                       
                   Relative gap is 0.00%.                                                          


Optimal solution found.

Intlinprog stopped at the root node because the objective value is within a gap tolerance of the optimal value,
options.AbsoluteGapTolerance = 0 (the default value). The intcon variables are integer within tolerance,
options.IntegerTolerance = 1e-05 (the default value).

解の表示 -- 誰がどのオフィスを獲得したか

numPeople = 7; office = cell(numPeople,1);
for i=1:numPeople
    office{i} = find(x(i:numPeople:end)); % people index in office
end

people = {'Mary Ann', 'Marjorie','  Tom   ',' Peter  ','Marcelo ',' Rakesh '};
for i=1:numPeople
    if isempty(office{i})
        name{i} = ' empty  ';
    else
        name{i} = people(office{i});
    end
end

printofficeassign(name);
title('Solution of the Office Assignment Problem');

解の質

この問題の場合、年功による選好の満足度が -fval の値まで最大化されます。exitflag = 1 は、intlinprog が最適解に収束したことを示します。出力構造体は、探索されたノードの数や分枝計算における下限と上限のギャップなど、解法プロセスに関する情報を提供します。この場合、分枝限定ノードは生成されませんでした。つまり、分枝限定ステップを経ずに問題が解かれました。ギャップは 0 です。これは、解が最適であり、目的関数で内部計算された下限と上限の間に差がないことを意味します。

fval,exitflag,output

fval = -33.8361

exitflag = 1

output = struct with fields:
        relativegap: 0
        absolutegap: 0
      numfeaspoints: 1
           numnodes: 0
    constrviolation: 0
            message: 'Optimal solution found.↵↵Intlinprog stopped at the root node because the objective value is within a gap tolerance of the optimal value, options.AbsoluteGapTolerance = 0 (the default value). The intcon variables are integer within tolerance, options.IntegerTolerance = 1e-05 (the default value).'