範囲制約付きの二次計画法、ソルバーベース

ライブスクリプトを開く

この例では、二次最適化問題を解いて、サーカスのテントの形状を決定する方法を説明します。テントは、弾性のある重い素材で形成されており、制約の下で位置エネルギーが最小になる形状になります。問題を離散化すると、範囲制約付きの二次計画法問題になります。

この例の問題ベースのバージョンについては、範囲制約付き二次計画法、問題ベースを参照してください。

問題の定義

正方形の区画にサーカスのテントを建築することを考えます。このテントには 5 本の柱があり、弾力性がある重い素材で覆われます。問題は、テントの自然な形状を求めることです。位置 p におけるテントの高さ x(p) として形状をモデル化します。

高さ x まで持ち上げた重い素材の位置エネルギーは、素材の重さに比例する定数 c に対して cx です。この問題では c = 1/3000 を選択します。

素材の一部分の弾性位置エネルギー $E_{s t r e t c h}$ は、素材の高さの 2 階微分に高さを乗算した値にほぼ比例します。2 階微分は、5 つの点の有限差分近似によって近似できます (有限差分ステップのサイズは 1 であると仮定します)。 $Δ x$ は 1 番目の座標方向における 1 単位のシフトを、 $Δ y$ は 2 番目の座標方向における 1 単位のシフトを表すとします。

$E_{s t r e t c h} (p) = (- 1 (x (p + Δ_{x}) + x (p - Δ_{x}) + x (p + Δ_{y}) + x (p - Δ_{y})) + 4 x (p)) x (p) .$

テントの自然な形状では、総位置エネルギーが最小になります。問題を離散化することにより、最小化対象の総位置エネルギーは、 $E_{s t r e t c h} (p)$ + cx(p) のすべての位置 p の合計であることがわかります。

この位置エネルギーは、変数 x による二次式です。

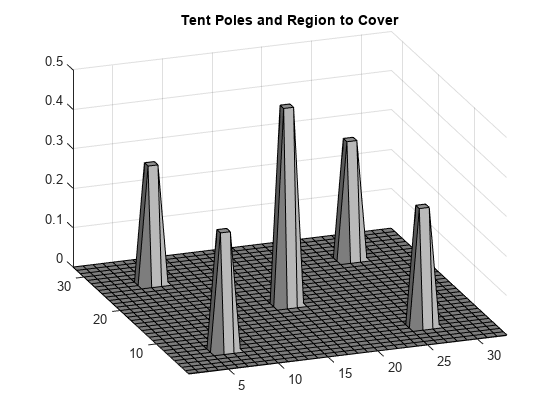
端におけるテントの高さがゼロであるという境界条件を指定します。テントの柱の断面積は 1 x 1 単位であり、テント全体のサイズは 33 x 33 単位です。各柱の高さと位置を指定します。正方形の区画の領域とテントの柱をプロットします。

height = zeros(33);
height(6:7,6:7) = 0.3;
height(26:27,26:27) = 0.3;
height(6:7,26:27) = 0.3;
height(26:27,6:7) = 0.3;
height(16:17,16:17) = 0.5;
colormap(gray);
surfl(height)
axis tight
view([-20,30]);
title('Tent Poles and Region to Cover')

境界条件の作成

行列 height は、解 x の下限を定義します。境界で解をゼロに制限するため、境界で上限 ub をゼロに設定します。

boundary = false(size(height));
boundary([1,33],:) = true;
boundary(:,[1,33]) = true;
ub = inf(size(boundary)); % No upper bound on most of the region
ub(boundary) = 0;

目的関数行列の作成

quadprog の問題定式化は、次を最小化することです。

$\frac{1}{2} x^{T} H x + f^{T} x$ .

このケースでは、線形項 $f^{T} x$ は素材の高さの位置エネルギーに対応します。したがって、x の各成分について f = 1/3000 を指定します。

f = ones(size(height))/3000;

関数 delsq を使用して、 $E_{s t r e t c h}$ を表す有限差分行列を作成します。関数 delsq の返すスパース行列には、 $E_{s t r e t c h} (p)$ の式の 4 および -1 というエントリに対応する、4 および -1 のエントリが含まれています。返された行列に 2 を乗算し、 $E_{s t r e t c h}$ によって与えられるエネルギー関数を使用して quadprog で二次計画法を解きます。

H = delsq(numgrid('S',33+2))*2;

行列 H の構造を表示します。この行列は x(:) に作用します。これは、行列 x が線形インデックスによりベクトルに変換されることを意味します。

spy(H);
title('Sparsity Structure of Hessian Matrix');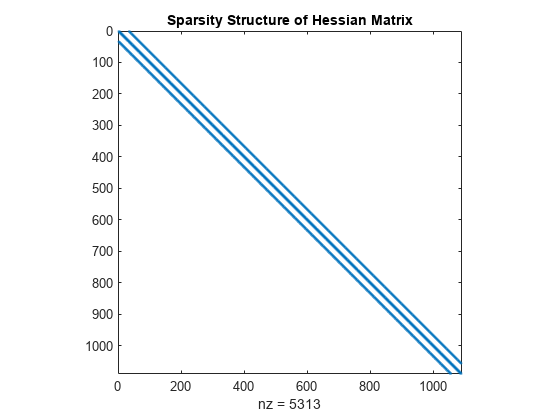

最適化ソルバーの実行

quadprog を呼び出して問題を解きます。

x = quadprog(H,f,[],[],[],[],height,ub);

Minimum found that satisfies the constraints.

Optimization completed because the objective function is non-decreasing in 
feasible directions, to within the value of the optimality tolerance,
and constraints are satisfied to within the value of the constraint tolerance.

解のプロット

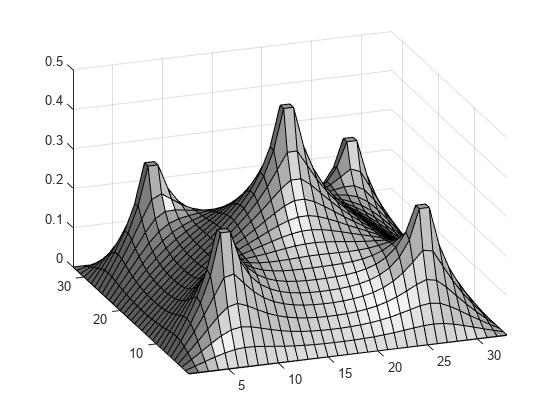
解 x を行列 S に形状変更します。次に、解をプロットします。

S = reshape(x,size(height));
surfl(S);
axis tight;
view([-20,30]);