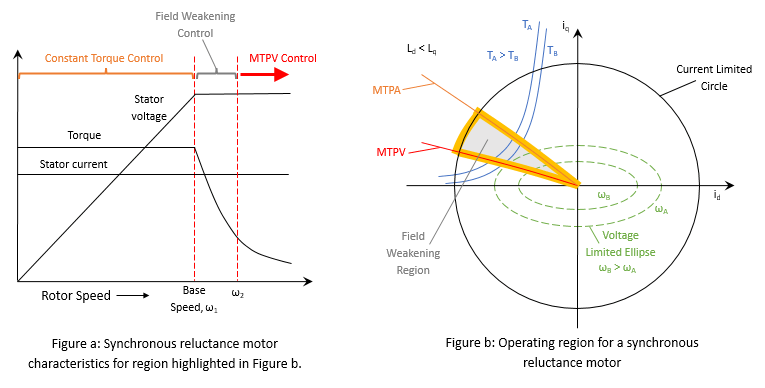
LUT based SynRM Control Reference
Generate lookup-table-based control reference currents for field-oriented control of SynRM and PMaSynRM
Since R2024a
Libraries:
Motor Control Blockset /
Controls /
Control Reference
Description
The LUT based SynRM Control Reference block generates the d-axis and q-axis reference currents for field-oriented control and field-weakening control of a synchronous reluctance motor (SynRM) and a permanent magnet-assisted synchronous reluctance motor (PMaSynRM). You can specify reference torque and feedback mechanical speed and the block outputs the corresponding reference current values. The block also supports the maximum torque per ampere (MTPA) and maximum torque per voltage (MTPV) operating regions.
The block uses id(T,ω) and iq(T,ω) lookup tables (LUTs) to generate reference current values. Depending on the input method you use to specify the motor parameters, the block can either generate LUTs or use the data you provide.
You can specify the motor parameters using one of these methods.
Note
The following equations for SynRM and PMaSynRM follow a d-q axis notation that is identical to that of a permanent magnet synchronous motor (PMSM).
Linear model with lumped parameters— Lumped parameters with Ld and Lq (for SynRM) or lumped parameters with Ld, Lq, and FluxPM (for PMaSynRM)This method uses the lumped parameters to compute the id and iq LUTs. The block obtains id and iq for the given ω and T inputs by solving the equations associated with these curves.
Maximum torque per ampere (MTPA) curve (for SynRM)
Maximum torque per ampere (MTPA) curve (for PMaSynRM)
Constant torque trajectory (for SynRM)
Constant torque trajectory (for PMaSynRM)
Current limit curve
Voltage limit curve (for SynRM)
Voltage limit curve (for PMaSynRM)
When the motor operates within the voltage constraints, the block solves for the intersection of the MTPA line and the constant torque trajectory.
When the motor operates beyond the voltage constraints, the block solves for the intersection of the voltage constraint curve and the constant torque trajectory.
After computing the id and iq tables from a grid of ω and T values, the block uses interpolation to find id ref and iq ref for any ω and T inputs that lie within the range of the table values. The table values are clipped for ω and T values beyond the boundaries.
Non-linear model with Ld and Lq LUTsorNon-linear model with Ld, Lq, and FluxPM LUTs— Nonlinear model with d-axis and q-axis stator winding inductances and permanent magnet flux linkage lookup tablesThis method uses an approach similar to the lumped parameters method, except that the block updates the values for Ld(id,iq), Lq(id,iq), and FluxPM(id,iq) each time it computes id and iq . The block iterates these computations until the id and iq values converge.
Note
FluxPM(id,iq) value is applicable only to a PMaSynRM. Ld(id,iq) and Lq(id,iq) values are applicable for both SynRM and PMaSynRM.
Non-linear model with D,Q-flux linkage LUTs— Nonlinear model with d-axis and q-axis flux linkage lookup tables.This method uses an approach similar to the lumped parameters method, except that the block updates the values for ψd(id,iq) and ψq(id,iq) each time it computes id and iq . The block iterates these computations until the id and iq values converge.
Non-linear model with id and iq LUTs— Use this method when you want to manually provide the id(T,ω) and iq(T,ω) tables. Typically, you obtain these tables through simulations or dyno tests.
You can also generate these tables using the mcb.generateMotorLUT
function in Motor Control Blockset™.
For a detailed set of equations and assumptions that Motor Control Blockset uses for a synchronous reluctance machine, see Synchronous Reluctance Machine (Simscape Electrical).
In addition, you can use the Vdc input method parameter to configure the block to accept a fixed reference DC voltage through the DC voltage to compute LUTs (V) parameter or a variable reference DC voltage through a separate input port Vdc .
Based on the method you select in the Motor parameter input method parameter, you can use the lumped parameters or a nonlinear model to compute the reference currents as shown in this table.
| Motor parameter input method | Vdc input method | Technique used to compute reference currents |
|---|---|---|
Linear model with lumped parameters
|
Specify via dialog
| The block uses the lumped parameters to compute the id and iq LUTs for a fixed voltage specified in the DC bus voltage, Vdc (V) parameter, using which it determines the reference currents. |
Input port - use 3D LUT (voltage slice
based)
| The block uses the lumped parameters to compute the 3-D id and iq LUTs containing data for different voltages (or voltage slices specified in the DC bus voltage breakpoint vector, Vdc (V) parameter). It uses this data to determine the reference currents corresponding to the voltage specified at the input port Vdc . | |
Input port - use 2D LUT (scaled-w
based)
| The block uses the lumped parameters to compute the 2-D id and iq LUTs for a fixed voltage specified in the DC bus voltage, Vdc (V) parameter. It uses these LUTs to compute the reference currents (corresponding to the voltage provided at the input port Vdc ) by scaling the speed (ω). | |
Non-linear model with D,Q-flux linkage LUTs
|
Specify via dialog
| The block computes the reference currents by using the d-axis and q-axis flux linkage LUTs for a fixed voltage specified in the DC bus voltage, Vdc (V) parameter. |
Input port - use 3D LUT (voltage slice
based)
| The block uses the 3-D d-axis and q-axis flux linkage LUTs containing data for different voltages (or voltage slices specified in the DC bus voltage breakpoint vector, Vdc (V) parameter). It uses these LUTs to compute the reference currents corresponding to the voltage provided at the input port Vdc . | |
Input port - use 2D LUT (scaled-w
based)
| The block uses the 2-D d-axis and q-axis flux linkage LUTs for a fixed voltage specified in the DC bus voltage, Vdc (V) parameter. It uses these LUTs to compute the reference currents (corresponding to the voltage provided at the input port Vdc ) by scaling the speed (ω). | |
Non-linear model with Ld and Lq LUTs
|
Specify via dialog
| The block computes the reference currents by using the given Ld and Lq LUTs for a fixed voltage specified in the DC bus voltage, Vdc (V) parameter. |
Input port - use 3D LUT (voltage slice based)
| The block uses the given 3-D Ld and Lq LUTs containing data for different voltages (or voltage slices specified in the DC bus voltage breakpoint vector, Vdc (V) parameter). It uses these LUTs to compute the reference currents corresponding to the voltage provided at the input port Vdc . | |
Input port - use 2D LUT (scaled-w based)
| The block uses the given 2-D Ld and Lq LUTs for a fixed voltage specified in the DC bus voltage, Vdc (V) parameter. It uses these LUTs to compute the reference currents (corresponding to the voltage provided at the input port Vdc ) by scaling the speed (ω). | |
Non-linear model with Ld, Lq, and FluxPM LUTs
|
Specify via dialog
| The block computes the reference currents by using the given Ld , Lq , and permanent magnet flux linkage LUTs for a fixed voltage specified in the DC bus voltage, Vdc (V) parameter. |
Input port - use 3D LUT (voltage slice
based)
| The block uses the given 3-D Ld , Lq , and permanent magnet flux linkage LUTs containing data for different voltages (or voltage slices specified in the DC bus voltage breakpoint vector, Vdc (V) parameter). It uses these LUTs to compute the reference currents corresponding to the voltage provided at the input port Vdc . | |
Input port - use 2D LUT (scaled-w
based)
| The block uses the given 2-D Ld , Lq , and permanent magnet flux linkage LUTs for a fixed voltage specified in the DC bus voltage, Vdc (V) parameter. It uses these LUTs to compute the reference currents (corresponding to the voltage provided at the input port Vdc ) by scaling the speed (ω). | |
Non-linear model with id and iq
LUTs
|
Specify via dialog
| The block determines the reference currents by using the given id , iq LUTs for a fixed voltage specified in the DC bus voltage, Vdc (V) parameter. |
Input port - use 3D LUT (voltage slice
based)
| The block uses the given 3-D id , iq LUTs containing data for different voltages (or voltage slices specified in the DC bus voltage breakpoint vector, Vdc (V) parameter). It uses these LUTs to determine the reference currents corresponding to the voltage provided at the input port Vdc . | |
Input port - use 2D LUT (scaled-w
based)
| The block uses the given 2-D id , iq LUTs for a fixed voltage specified in the DC bus voltage, Vdc (V) parameter. It uses these LUTs to compute the reference currents (corresponding to the voltage provided at the input port Vdc ) by scaling the speed (ω). |
Examples
Ports
Input
Output
Parameters
Extended Capabilities
Version History
Introduced in R2024a