このページの内容は最新ではありません。最新版の英語を参照するには、ここをクリックします。

高精度な演算によりほとんど整数を求める

この例では、Symbolic Math Toolbox™ の可変精度の算術を使用して、"ほとんど整数" (整数に非常に近い数) を見つける方法を説明します。この例では、整数 n = 1, ..., 200 について、exp(pi*sqrt(n)) または exp(pi*n) の形式をもつほとんど整数を検索します。

ほとんど整数

既定の設定では、MATLAB® は 16 桁の精度を使用しています。より高い精度の場合は、Symbolic Math Toolbox の関数 vpa を使用します。vpa は、数値を評価する際に精度を上げることができる可変精度を備えています。

まず、ほとんど整数 [2] のよく知られた例、すなわち実数 exp(pi*sqrt(163)) について考えます。この実数を正確なシンボリック数として作成します。

r = exp(pi*sqrt(sym(163)))

 
r =
 
exp(pi*163^(1/2))
 

vpa を使用して、この数を可変精度の算術で評価します。既定では、vpa は有効桁数 32 桁まで値を評価します。

f = vpa(r)

 
f =
 
262537412640768743.99999999999925
 

関数 digits を使用して有効桁数を変更できます。同じ数を有効桁数 25 桁で評価します。

digits(25)
f = vpa(r)

 
f =
 
262537412640768744.0
 

この数は整数に非常に近くなっています。この実数および最も近い整数との差を調べます。vpa を使用して、差を有効桁数 25 桁で評価します。

dr = vpa(round(r)-r)

 
dr =
 
0.0000000000007425171588693046942353249
 

exp(pi*sqrt(n) 形式のほとんど整数

整数 n = 1, ..., 200 について、exp(pi*sqrt(n)) の形式をもつほとんど整数を検索します。これらの数を正確なシンボリック数として作成します。

A = exp(pi*sqrt(sym(1:200)));

整数部の桁数が exp(pi*sqrt(200)) 桁にさらに 20 桁を加えた数となるように、有効桁数を設定します。

d = log10(A(end));
digits(ceil(d)+20)

この数字列および最も近い整数との差を評価します。丸め誤差が 0.0001 未満となるほとんど整数を見つけます。これらのほぼ整数を厳密なシンボリック型で表示します。

B = vpa(round(A)-A);
A_nearint = A(abs(B)<0.0001)'

 
A_nearint =
 
 exp(pi*37^(1/2))
 exp(pi*58^(1/2))
 exp(pi*67^(1/2))
exp(pi*163^(1/2))
 

差のヒストグラムをプロットします。この分布は、0 に近い差の度数が多いことを示しています。これは、exp(pi*sqrt(n)) の形式がほとんど整数である場所です。

histogram(double(B),100)

exp(pi*n 形式のほとんど整数

整数 n = 1, ..., 200 について、exp(pi*n) の形式をもつほとんど整数を検索します。これらの数を正確なシンボリック数として作成します。

A = exp(pi*sym(1:200));

整数部の桁数が exp(pi*200) 桁にさらに 20 桁を加えた数となるように、有効桁数を設定します。

d = log10(A(end));
digits(ceil(d)+20)

この数字列および最も近い整数との差を評価します。丸め誤差が 0.0001 未満となるほとんど整数を見つけます。結果は空の配列 sym となります。つまり、この数列にはこの条件を満たす数値がないことを意味します。

B = vpa(round(A)-A);
A_nearint = A(abs(B)<0.0001)

 
A_nearint =
 
Empty sym: 1-by-0
 

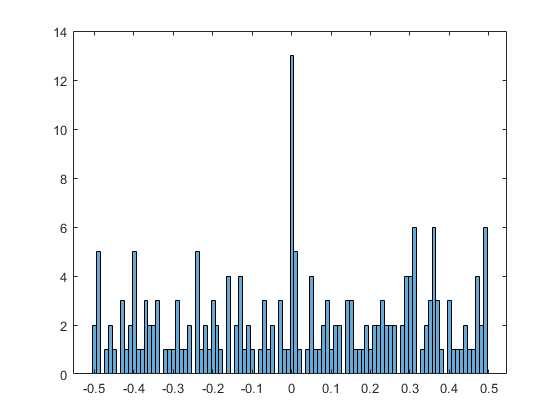
差のヒストグラムをプロットします。比較的均等に分布しているこのヒストグラムは、exp(pi*n) の形式がほとんど整数となる場合があまりないことを示しています。この特定の例では、丸め誤差が 0.0001 未満であるほとんど整数が存在しません。

histogram(double(B),100)

最後に、既定の精度である有効桁数 32 桁に戻して計算を続けます。

digits(32)

参考文献

[1] "Integer Relation Algorithm." In Wikipedia, April 9, 2022. https://en.wikipedia.org/w/index.php?title=Integer_relation_algorithm&oldid=1081697113.

[2] "Almost Integer." In Wikipedia, December 4, 2021. https://en.wikipedia.org/w/index.php?title=Almost_integer&oldid=1058543590.