Delaunay 三角形分割の作成と編集

ライブスクリプトを開く

この例では、delaunayTriangulation クラスを使用して Delaunay 三角形分割の作成、編集、クエリを行う方法を示します。Delaunay 三角形分割は、科学計算で最も広く使われている三角形分割です。三角形分割に関するプロパティは、さまざまな幾何学的な問題を解決するための基礎を提供します。中心軸の計算やメッシュのモーフィングに関するアプリケーションを使って、制約付き Delaunay 三角形分割の作成についても示します。

例 1: 2 次元 Delaunay 三角形分割の作成とプロット

この例では、2 次元 Delaunay 三角形分割を計算し、続いて頂点と三角形のラベルと共に三角形分割をプロットする方法を示します。

rng default
x = rand(10,1);
y = rand(10,1);
dt = delaunayTriangulation(x,y)

dt = 
  delaunayTriangulation with properties:

              Points: [10x2 double]
    ConnectivityList: [11x3 double]
         Constraints: []

triplot(dt)

プロットで頂点と三角形のラベルを表示します。

hold on
vxlabels = arrayfun(@(n) {sprintf('P%d', n)}, (1:10)');
Hpl = text(x,y,vxlabels,'FontWeight','bold','HorizontalAlignment',...
   'center','BackgroundColor','none');
ic = incenter(dt);
numtri = size(dt,1);
trilabels = arrayfun(@(x) {sprintf('T%d',x)}, (1:numtri)');
Htl = text(ic(:,1),ic(:,2),trilabels,'FontWeight','bold', ...
   'HorizontalAlignment','center','Color','blue');
hold off

Figure contains an axes object. The axes object contains 22 objects of type line, text.

例 2: 3 次元 Delaunay 三角形分割の作成とプロット

この例では、3 次元 Delaunay 三角形分割を計算してプロットする方法を示します。

rng default
X = rand(10,3);
dt = delaunayTriangulation(X)

dt = 
  delaunayTriangulation with properties:

              Points: [10x3 double]
    ConnectivityList: [18x4 double]
         Constraints: []

tetramesh(dt)
view([10 20])

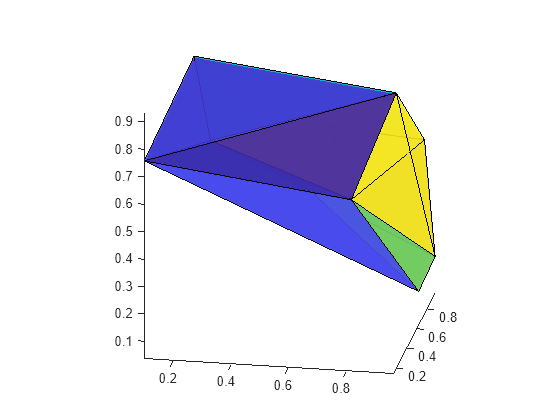
Figure contains an axes object. The axes object contains 18 objects of type patch.

大きな四面体メッシュを表示するには、convexHull メソッドを使用して境界の三角形分割を計算し、trisurf を使用してそれをプロットします。次に例を示します。

triboundary = convexHull(dt);
trisurf(triboundary, X(:,1), X(:,2), X(:,3),'FaceColor','cyan')

例 3: 三角形分割データの構造体へのアクセス

三角形分割データの構造体にアクセスする 2 つの方法があります。1 つ目の方法は Triangulation プロパティを使用し、2 つ目の方法はインデックスを使用します。

10 個の乱数点から 2 次元 Delaunay 三角形分割を作成します。

rng default
X = rand(10,2);
dt = delaunayTriangulation(X)

dt = 
  delaunayTriangulation with properties:

              Points: [10x2 double]
    ConnectivityList: [11x3 double]
         Constraints: []

三角形分割データの構造体にアクセスする 1 つの方法は、ConnectivityList プロパティを使用することです。

dt.ConnectivityList

ans = 11×3

     8     2     3
     6     7     3
     5     2     8
     7     8     3
     7     5     8
     7     6     1
     4     7     1
     9     5     4
     4     5     7
     9     2     5
      ⋮

インデックス付けは、三角形分割をクエリするための簡略化した方法です。構文は dt(i,j) です。ここで、j は i 番目の三角形の j 番目の頂点です。標準的なインデックス付けルールが適用されます。

インデックス付けを使用して三角形分割データの構造体をクエリします。

dt(:,:)

ans = 11×3

     8     2     3
     6     7     3
     5     2     8
     7     8     3
     7     5     8
     7     6     1
     4     7     1
     9     5     4
     4     5     7
     9     2     5
      ⋮

2 番目の三角形は以下のとおりです。

dt(2,:)

ans = 1×3

     6     7     3

2 番目の三角形の 3 番目の頂点は以下のとおりです。

dt(2,3)

ans = 3

最初の 3 つの三角形は以下のとおりです。

dt(1:3,:)

ans = 3×3

     8     2     3
     6     7     3
     5     2     8

例 4: 点を挿入または削除するための Delaunay 三角形分割の編集

この例は、点を挿入または削除するために、インデックスベースの添字を使用する方法を示します。小さな変更であれば、新たな delaunayTriangulation をゼロから再作成するよりも、delaunayTriangulation を編集した方がより効率的になります。これは、データセットが大きい場合に特に言えることです。

単位正方形内にある 10 個の乱数点から Delaunay 三角形分割を作成します。

rng default
x = rand(10,1);
y = rand(10,1);
dt = delaunayTriangulation(x,y)

dt = 
  delaunayTriangulation with properties:

              Points: [10x2 double]
    ConnectivityList: [11x3 double]
         Constraints: []

5 個の追加の乱数点を挿入します。

dt.Points(end+(1:5),:) = rand(5,2)

dt = 
  delaunayTriangulation with properties:

              Points: [15x2 double]
    ConnectivityList: [20x3 double]
         Constraints: []

5 番目の点を置き換えます。

dt.Points(5,:) = [0 0]

dt = 
  delaunayTriangulation with properties:

              Points: [15x2 double]
    ConnectivityList: [20x3 double]
         Constraints: []

4 番目の点を削除します。

dt.Points(4,:) = []

dt = 
  delaunayTriangulation with properties:

              Points: [14x2 double]
    ConnectivityList: [18x3 double]
         Constraints: []

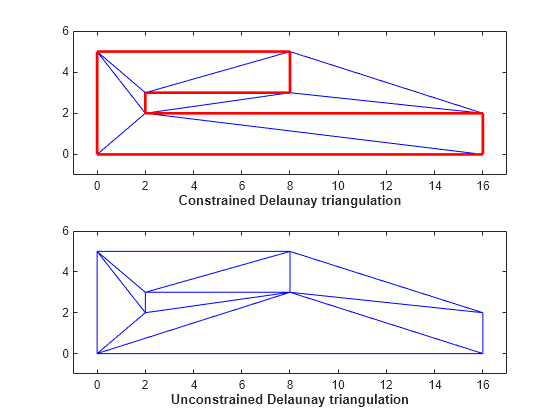
例 5: 制約付き Delaunay 三角形分割の作成

この例では、制約付き Delaunay 三角形分割を作成する方法を示し、制約の効果を示します。

制約付き Delaunay 三角形分割を作成してプロットします。

X = [0 0; 16 0; 16 2; 2 2; 2 3; 8 3; 8 5; 0 5];
C = [1 2; 2 3; 3 4; 4 5; 5 6; 6 7; 7 8; 8 1];
dt = delaunayTriangulation(X,C);
subplot(2,1,1)
triplot(dt)
axis([-1 17 -1 6])
xlabel('Constrained Delaunay triangulation','FontWeight','b')

制約付きのエッジを赤色でプロットします。

hold on
plot(X(C'),X(C'+size(X,1)),'-r','LineWidth',2)
hold off

ここで、制約を削除し、制約なしの Delaunay 三角形分割をプロットします。

dt.Constraints = [];
subplot(2,1,2)
triplot(dt)
axis([-1 17 -1 6])
xlabel('Unconstrained Delaunay triangulation','FontWeight','b')

Figure contains 2 axes objects. Axes object 1 contains 9 objects of type line. Axes object 2 contains an object of type line.

例 6: 地図の制約付き Delaunay 三角形分割の作成

隣接する米国の周辺部の地図を読み込みます。多角形を表す制約付き Delaunay 三角形分割を作成します。この三角形分割は、点集合の凸包で囲まれた領域にまたがります。多角形の領域内にある三角形を除去し、プロットします。メモ: データセットは重複するデータ点を含んでいます。すなわち、2 つ以上のデータ点が同じ位置にあります。重複する点を取り除いてから、delaunayTriangulation はそれに応じて制約を再度形成します。

clf
load usapolygon

多角形の境界を構成する連続する 2 点間のエッジ制約を定義し、Delaunay 三角形分割を作成します。

nump = numel(uslon);
C = [(1:(nump-1))' (2:nump)'; nump 1];
dt = delaunayTriangulation(uslon,uslat,C);

Warning: Duplicate data points have been detected and removed.
 The Triangulation indices and constraints are defined with respect to the unique set of points in delaunayTriangulation.

Warning: Intersecting edge constraints have been split, this may have added new points into the triangulation.

io = isInterior(dt);
patch('Faces',dt(io,:),'Vertices',dt.Points,'FaceColor','r')
axis equal
axis([-130 -60 20 55])
xlabel('Constrained Delaunay Triangulation of usapolygon','FontWeight','b')

Figure contains an axes object. The axes object contains an object of type patch.

例 7: 点群から曲線を再構成

この例は、点群から多角形の境界を再構成するための Delaunay 三角形分割の使用方法を示します。再構成は Crust アルゴリズムに基づきます。

参照: N. Amenta, M. Bern, and D. Eppstein.The crust and the beta-skeleton:combinatorial curve reconstruction.Graphical Models and Image Processing, 60:125-135, 1998.

点群を表す点集合を作成します。

numpts = 192;
t = linspace( -pi, pi, numpts+1 )';
t(end) = [];
r = 0.1 + 5*sqrt( cos( 6*t ).^2 + (0.7).^2 );
x = r.*cos(t);
y = r.*sin(t);
ri = randperm(numpts);
x = x(ri);
y = y(ri);

その点集合の Delaunay 三角形分割を作成します。

dt = delaunayTriangulation(x,y);
tri = dt(:,:);

ボロノイ頂点の位置を既存の三角形分割に挿入します。

V = voronoiDiagram(dt);

unique を使用して、無限遠頂点を削除し、重複する点をフィルターで除外します。

V(1,:) = [];
numv = size(V,1);
dt.Points(end+(1:numv),:) = unique(V,'rows');

サンプル点のペアを接続する Delaunay エッジは境界を表します。

delEdges = edges(dt);
validx = delEdges(:,1) <= numpts;
validy = delEdges(:,2) <= numpts;
boundaryEdges = delEdges((validx & validy),:)';
xb = x(boundaryEdges);
yb = y(boundaryEdges);
clf
triplot(tri,x,y)
axis equal
hold on
plot(x,y,'*r')
plot(xb,yb,'-r')
xlabel('Curve reconstruction from point cloud','FontWeight','b')
hold off

Figure contains an axes object. The axes object contains 194 objects of type line.

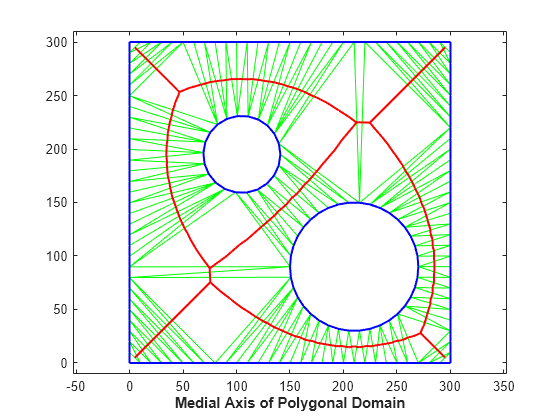
例 8: 多角形領域の近似の中心軸の計算

この例では、制約付き Delaunay 三角形分割を使って多角形領域の近似の中心軸を作成する方法を示します。多角形の "中心軸" は、多角形内部の最大の円盤形の中心の位置で定義されます。

領域の境界線上の点のサンプルの制約付き Delaunay 三角形分割を作成します。

load trimesh2d
dt = delaunayTriangulation(x,y,Constraints);
inside = isInterior(dt);

領域の三角形を表す三角形分割を作成します。

tr = triangulation(dt(inside,:),dt.Points);

近傍三角形の外心を結ぶ一連のエッジを作成します。追加のロジックにより、そのような一意の一連のエッジが作成されます。

numt = size(tr,1);
T = (1:numt)';
neigh = neighbors(tr);
cc = circumcenter(tr);
xcc = cc(:,1);
ycc = cc(:,2);
idx1 = T < neigh(:,1);
idx2 = T < neigh(:,2);
idx3 = T < neigh(:,3);
neigh = [T(idx1) neigh(idx1,1); T(idx2) neigh(idx2,2); T(idx3) neigh(idx3,3)]';

領域の三角形を緑色で、領域の境界線を青色で、中心軸を赤色でプロットします。

clf
triplot(tr,'g')
hold on
plot(xcc(neigh), ycc(neigh), '-r','LineWidth',1.5)
axis([-10 310 -10 310])
axis equal
plot(x(Constraints'),y(Constraints'),'-b','LineWidth',1.5)
xlabel('Medial Axis of Polygonal Domain','FontWeight','b')
hold off

Figure contains an axes object. The axes object contains 364 objects of type line.

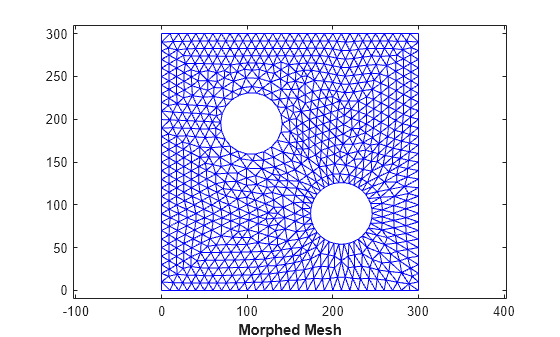
例 9: 2 次元メッシュを変更した境界に変形

この例では、領域の境界線への変更を適用するために 2 次元領域のメッシュを変形する方法を示します。

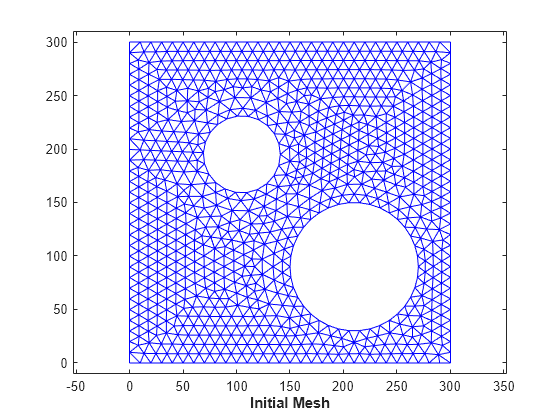
手順 1: データを読み込みます。変形するメッシュは、面と頂点の形式の三角形分割 trife、xfe、yfe で定義されます。

load trimesh2d
clf
triplot(trife,xfe,yfe)
axis equal
axis([-10 310 -10 310])
axis equal
xlabel('Initial Mesh','FontWeight','b')

Figure contains an axes object. The axes object contains an object of type line.

手順 2: 背景の三角形分割 - メッシュの境界を表す点集合の制約付き Delaunay 三角形分割を作成します。メッシュの頂点ごとに、背景の三角形分割に対して位置を定義する記述子を計算します。記述子はその三角形に対して重心座標と共に囲まれた三角形を表します。

dt = delaunayTriangulation(x,y,Constraints);
clf
triplot(dt)
axis equal
axis([-10 310 -10 310])
axis equal
xlabel('Background Triangulation','FontWeight','b')

Figure contains an axes object. The axes object contains an object of type line.

descriptors.tri = pointLocation(dt,xfe,yfe);
descriptors.baryCoords = cartesianToBarycentric(dt,descriptors.tri,[xfe yfe]);

手順 3: 領域の境界線の変更を取り込むために、背景の三角形分割を編集します。

cc1 = [210 90];
circ1 = (143:180)';
x(circ1) = (x(circ1)-cc1(1))*0.6 + cc1(1);
y(circ1) = (y(circ1)-cc1(2))*0.6 + cc1(2);
tr = triangulation(dt(:,:),x,y);
clf
triplot(tr)
axis([-10 310 -10 310])
axis equal
xlabel('Edited Background Triangulation - Hole Size Reduced','FontWeight','b')

Figure contains an axes object. The axes object contains an object of type line.

手順 4: 評価の根拠として、変形した背景の三角形分割を使用し、記述子を直交座標に戻します。

Xnew = barycentricToCartesian(tr,descriptors.tri,descriptors.baryCoords);
tr = triangulation(trife,Xnew);
clf
triplot(tr)
axis([-10 310 -10 310])
axis equal
xlabel('Morphed Mesh','FontWeight','b')

Figure contains an axes object. The axes object contains an object of type line.