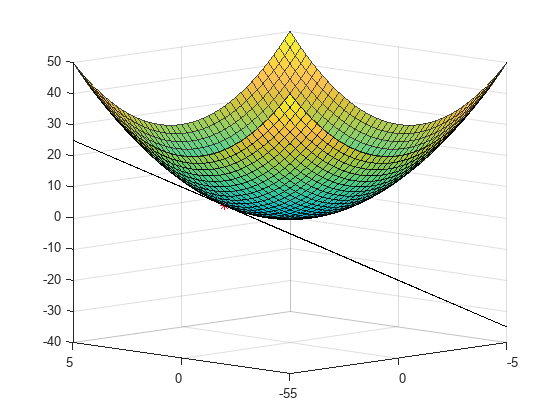
表面に対する正接面の計算

この例では、有限差分によって関数の勾配を近似する方法を説明します。次に、これらの近似勾配を使用して、表面上の点に対して正接面をプロットする方法を示します。

関数ハンドルを使用して、関数 $$f(x,y)=x^2+y^2$$ を作成します。

f = @(x,y) x.^2 + y.^2;

関数 gradient を使用して、$$x$$ および $$y$$ についての $$f(x,y)$$ の偏導関数を近似します。メッシュ サイズと同じ長さの有限差分を指定します。

[xx,yy] = meshgrid(-5:0.25:5);
[fx,fy] = gradient(f(xx,yy),0.25);

表面上の点 $$P=(x_0,y_0,f(x_0,y_0))$$ に対する正接面は次の式で与えられます。

$$z=f(x_0,y_0)+\frac{\partial f(x_0,y_0)}{\partial x}(x-x_0)+\frac{\partial f(x_0,y_0)}{\partial y}(y-y_0).$$

行列 fx と fy は偏導関数 $$\frac{\partial f}{\partial x}$$ および $$\frac{\partial f}{\partial y}$$ に対する近似です。この例の注目点は、正接面が関数の表面に接する点であり、(x0,y0) = (1,2) です。この注目点における関数値は f(1,2) = 5 です。

正接面 z を近似するには、この注目点における微分値を求める必要があります。この点のインデックスを取得し、そこで近似微分を求めます。

x0 = 1;
y0 = 2;
t = (xx == x0) & (yy == y0);
indt = find(t);
fx0 = fx(indt);
fy0 = fy(indt);

正接面 z の方程式を使用して関数ハンドルを作成します。

z = @(x,y) f(x0,y0) + fx0*(x-x0) + fy0*(y-y0);

元の関数 $$f(x,y)$$、点 P、および P において関数に接する部分平面 z をプロットします。

surf(xx,yy,f(xx,yy),'EdgeAlpha',0.7,'FaceAlpha',0.9)
hold on
surf(xx,yy,z(xx,yy))
plot3(1,2,f(1,2),'r*')

側面を表示します。

view(-135,9)

参考

gradient

関連するトピック

• 関数ハンドルの作成