相関のある変数の特定と可視化
データ変数間の関係を解析する際に、相関のある変数を特定して可視化し、データ セットに関する洞察を得ることができます。この例では、corrcoef 関数を使用して相関係数を計算し、関係の強さと方向を判別する方法を示します。相関係数の範囲は -1 から 1 です。以下のようになります。
1 に近い値は、データ変数間に正の線形関係があることを示します。
–1 に近い値は、データ変数間に負の線形関係 ("反相関") があることを示します。
0 に近い値または 0 は、データ変数間に線形関係がないことを示します。
さらに、この例では、有意な相関を判別し、相関性の最も高いペアを特定する方法を示します。この例では、ヒートマップと棒グラフを使用して相関をプロットし、変数間の関係を視覚的に比較できます。
相関係数と p 値の計算
変数間の相関を含むランダム データを生成します。次に、corrcoef 関数を使用して、相関係数と、相関の有意性を示す対応する p 値を計算します。
rng(16) A = randn(50,6); A(:,3) = A(:,3) + 2*A(:,1); A(:,4) = A(:,4) - 3*A(:,2); A(:,5) = A(:,6) + 0.1*A(:,4) - 0.1*A(:,3); [R,P] = corrcoef(A)
R = 6×6
1.0000 -0.1248 0.8047 0.1300 -0.1726 -0.1009
-0.1248 1.0000 -0.0744 -0.9612 -0.2314 0.0730
0.8047 -0.0744 1.0000 0.0709 -0.3595 -0.2515
0.1300 -0.9612 0.0709 1.0000 0.2611 -0.0549
-0.1726 -0.2314 -0.3595 0.2611 1.0000 0.9384
-0.1009 0.0730 -0.2515 -0.0549 0.9384 1.0000
P = 6×6
1.0000 0.3878 0.0000 0.3683 0.2308 0.4858
0.3878 1.0000 0.6075 0.0000 0.1060 0.6143
0.0000 0.6075 1.0000 0.6248 0.0103 0.0781
0.3683 0.0000 0.6248 1.0000 0.0670 0.7051
0.2308 0.1060 0.0103 0.0670 1.0000 0.0000
0.4858 0.6143 0.0781 0.7051 0.0000 1.0000
返される行列 R と P はそれぞれ相関係数と p 値を含んでおり、対称行列です。R の下三角部分を抽出して、一意のペアワイズ相関に焦点を当てます。
R = tril(R,-1)
R = 6×6
0 0 0 0 0 0
-0.1248 0 0 0 0 0
0.8047 -0.0744 0 0 0 0
0.1300 -0.9612 0.0709 0 0 0
-0.1726 -0.2314 -0.3595 0.2611 0 0
-0.1009 0.0730 -0.2515 -0.0549 0.9384 0
ヒートマップを使用した相関の可視化
相関係数のヒートマップを作成して、変数間の関係の強さと方向を可視化します。
相関係数行列のゼロ (下三角部分の相関の冗長要素を示す) を欠損値 (NaN) に変換します。次に、負の相関をもつ変数のペアを赤、正の相関をもつ変数のペアを青、相関のない変数のペアを白で示すカラーマップを作成します。ヒートマップでは、最も強い相関が明るい赤および明るい青で強調表示されます。
Rheatmap = standardizeMissing(R,0);
map = [1 0 0;
0.9 0.3 0.3;
0.9 0.6 0.6;
1 1 1;
0.6 0.6 0.9;
0.3 0.3 0.9;
0 0 1];
h = heatmap(Rheatmap,Colormap=map,ColorLimits=[-1 1]);
h.Title = "Correlation Coefficients";
h.YLabel = "First Variable";
h.XLabel = "Second Variable";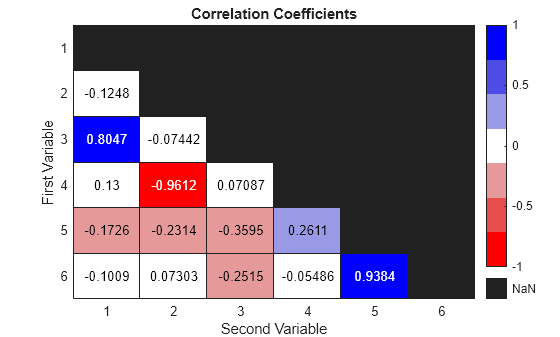
有意な相関の判別
p 値が 0.05 を超える相関を除外して、有意な相関を特定します。この手法により、解析の焦点を統計的に有意な関係のみに合わせ、ランダム ノイズを相関として解釈することを回避します。
threshold = 0.05; R(abs(P) > threshold) = 0; [firstVar,secondVar,corrCoef] = find(R)
firstVar = 4×1
3
4
5
6
secondVar = 4×1
1
2
3
5
corrCoef = 4×1
0.8047
-0.9612
-0.3595
0.9384
表での相関の表示
有意な相関を表にまとめ、インデックス、相関係数、および p 値も含めます。
ind2 = sub2ind(size(P),firstVar,secondVar); sigP = P(ind2); TSig = table(firstVar,secondVar,corrCoef,sigP)
TSig=4×4 table
firstVar secondVar corrCoef sigP
________ _________ ________ __________
3 1 0.80471 1.8997e-12
4 2 -0.96118 1.7065e-28
5 3 -0.35949 0.010346
6 5 0.9384 8.5819e-24
相関の強さ順に上位 3 つの相関をリストします。上位の相関は、入力データで設定された関係と一致しています。
A(:,3) = A(:,3) + 2*A(:,1); A(:,4) = A(:,4) - 3*A(:,2); A(:,5) = A(:,6) + 0.1*A(:,4) - 0.1*A(:,3);
k = 3; TTopk = topkrows(TSig,k,"corrCoef","descend",ComparisonMethod="abs")
TTopk=3×4 table
firstVar secondVar corrCoef sigP
________ _________ ________ __________
4 2 -0.96118 1.7065e-28
6 5 0.9384 8.5819e-24
3 1 0.80471 1.8997e-12
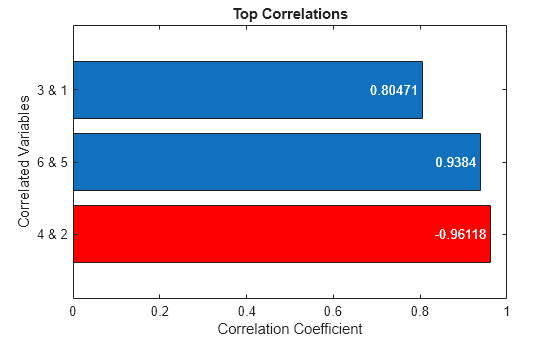
棒グラフを使用した上位の相関の可視化
横棒グラフを使用して、最も有意な 3 つの相関を表示します。負の相関は赤いバーで、正の相関は青いバーで表します。
labels = TTopk.firstVar + " & " + TTopk.secondVar; b = barh(labels,abs(TTopk.corrCoef)); negCorr = TTopk.corrCoef < 0; b.FaceColor = "flat"; b.CData(negCorr,:) = repmat([1 0 0],nnz(negCorr),1); b.Labels = TTopk.corrCoef; b.LabelLocation = "end-inside"; title("Top Correlations") xlabel("Correlation Coefficient") ylabel("Correlated Variables")