Cooling Tower (TL-MA)
Libraries:
Simscape /
Fluids /
Heat Exchangers /
Thermal Liquid - Moist Air
Description
The Cooling Tower (TL-MA) block models a cooling tower between moist air and a thermal liquid network. The block models sensible and latent heat transfer from the thermal liquid side to the moist air side based on an analogous effectiveness-NTU method for heat and water vapor mass transfer. The thermal liquid side represents the water in the tower while the moist air side represents the environmental air. The block is performance based rather than geometry based, which means that the block sizes the cooling tower to match the nominal operating conditions that you specify.
Cooling Tower Geometry
Large HVAC systems use cooling towers to reject heat from water to the environment in applications where the amount of heat is too large for regular water-air heat exchangers to be practical. In a cooling tower, the hot water and air are in direct contact, which allows some of the water to evaporate into the air and cools the rest of the water by the evaporative cooling effect.
A cooling tower works by spreading and spraying hot water from the top of the tower over a large area to encourage it to evaporate into the air. Typically, there is a fill material underneath the spray nozzles with a large surface area that allows the water to form a thin film and spread out. The fill material increases the contact area between the water and the air for more evaporation. Because there is no heat source, the latent heat needed to turn liquid water into water vapor comes from the water itself. As a result, the water that did not evaporate cools. The cold water collects at the bottom of the cooling tower in a basin, and can be returned to the HVAC system.
You can use the Flow arrangement parameter to specify if the cooling tower uses a cross flow or counter flow. This block only models direct-flow cooling towers, which means the water is in direct contact with the air. The block also only models mechanical-draft cooling towers, where a fan moves the air through the cooling tower.
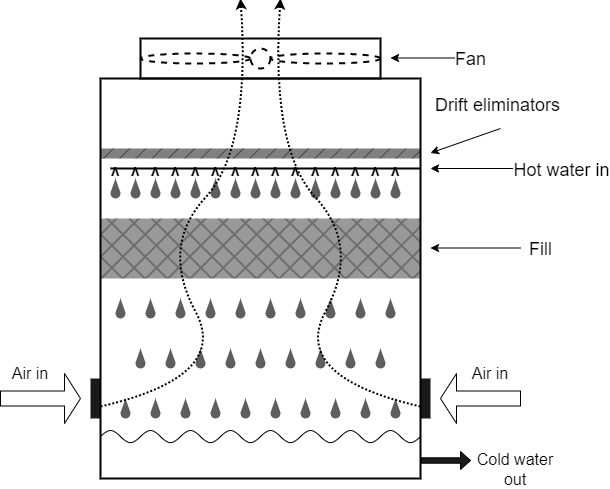
This figure shows a diagram of a counter-flow, direct-contact, induced mechanical-draft cooling tower.
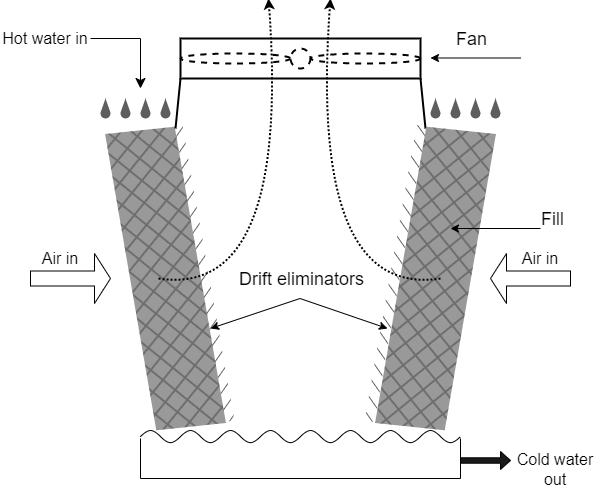
This figure shows a diagram of a direct-contact, induced mechanical-draft cooling tower with two air entries.
Heat Transfer and Evaporation Rate
The combined heat and water vapor mass transfer is
where:
Qcombined,max is the theoretically maximum combined heat and water vapor mass transfer,
sTLin is the enthalpy of the saturated moist air evaluated at the temperature of the inlet at the thermal liquid side.
MAin is the mixture enthalpy of the moist air at the inlet.
Cmin is the smaller capacity ratio between the moist air and thermal liquid.
When Flow arrangement is Counter
flow, the effectiveness factor, ε, is
where CR is the capacity ratio and NTU is the number of transfer units.
When Flow arrangement is Cross
flow, the block assumes that one fluid is mixed and the other is
unmixed. If the fluid with the lower value for C is
unmixed,
Typically, the moist air will have the lower value for C. If the fluid with the lower value for C is mixed,
The capacity ratio is
CMA and CTL are the capacity rates for the moist air and thermal liquid, respectively,
where:
ṁTL is the thermal liquid mass flow rate.
cpTL is the thermal liquid specific heat at constant pressure.
ṁagMA is the mass flow rate of the dry air and trace gas.
The number of transfer units, NTU, is
where:
A is the heat transfer surface area.
UMA is the heat transfer conductance on the moist air side.
pMA is the moist air specific heat at constant pressure.
The combined heat and water vapor mass transfer, Qcombined, accounts for the sensible heat transfer, latent heat, and energy debit due to lost liquid,
where:
Q is the sensible heat transfer between thermal liquid and moist air in the cooling tower. The block calculates this value with . This term represents the portion of the cooling due to the temperature difference between the thermal liquid and moist air.
Δhfgeff is the water vapor specific enthalpy of vaporization. When multiplied by ṁe, this term gives the latent heat transfer between the thermal liquid and moist air in the cooling tower. This term represents the portion of the cooling due to the energy extracted from the liquid water when converted into water vapor.
hleff is the liquid water specific enthalpy. When multiplied by ṁe, this term gives the energy debited from the energy balance of the thermal liquid flow due to the removal of a portion of the liquid.
The evaporation rate in the cooling tower is
where:
Wseff is the effective saturated humidity ratio.
WMAin is the humidity ratio at the moist air inlet.
The effective saturated humidity ratio is
where:
Ra is the specific gas constant of dry air.
G is the trace gas ratio.
Rg is the specific gas constant of the trace gas.
RW is the specific gas constant of the water vapor.
p is the pressure.
φws is the value of the Relative humidity at saturation parameter.
pws(Teff) is the water vapor saturation pressure evaluated at the effective liquid film surface temperature.
The effective liquid film surface temperature is
where:
TTLin is the temperature of the thermal liquid at the inlet.
sTL is the specific heat of the saturated moist air along the saturation curve when evaluated at the temperature of the thermal liquid.
seff is the saturated mixture enthalpy along the liquid film surface
The heat transfer conductance at the moist air side, UMAA, is
where:
UMA is the heat transfer coefficient.
ṁMA is the moist air mass flow rate.
μMA is the moist air dynamic viscosity.
a is the coefficient for the proportionality in the Nusselt number correlation.
b is the coefficient for the Reynolds number exponent in the Nusselt number correlation.
c is the coefficient for the Prandtl number exponent in the Nusselt number correlation.
PrMA is the moist air Prandtl number.
kMA is the thermal conductivity of the moist air.
Dref is an arbitrary diameter. The block uses this value with Sref to nondimensionalize with respect to length.
Sref is the flow area corresponding to Dref.
Nulam is 3.66, which is the theoretical Nusselt number for a laminar flow through a circular pipe.
Gfill is the geometry scale factor for the cooling tower fill material. The block calculates this value at nominal operating conditions.
Cooling Tower Sizing
The block sizes the cooling tower to match the nominal performance at nominal operating conditions. On the thermal liquid side, the Nominal capacity specification parameter specifies how the block determines the nominal data:
Water mass flow rateorWater volumetric flow rate— The block infers the nominal capacity from the nominal flow rate and the nominal inlet and outlet temperatures.Rate of cooling in cooling towerorRate of cooling in evaporator— The block infers the nominal flow rate from the nominal capacity.
On the moist air side, the nominal data depends on the Specify full moist air nominal conditions parameter.
If you clear the Specify full moist air nominal conditions check box, the only nominal condition you specify is the value of the Nominal inlet wet-bulb temperature parameter. Use this option if your manufacturer datasheet provides only the nominal wet-bulb temperature. The block calculates the other nominal conditions:
The block calculates the nominal inlet temperature based on the value of the Nominal inlet wet-bulb temperature parameter so that the relative humidity is 50%.
The block calculates the nominal flow rate from the nominal water flow rate so that the capacity ratio at nominal operating condition is
1.
The block assumes that the nominal inlet pressure is atmospheric and that there is no nominal trace gas..
If you select Specify full moist air nominal conditions, you must specify the nominal inlet pressure, nominal inlet temperature, nominal inlet humidity level, and nominal inlet trace gas level.
The block uses nominal operating conditions to solve for the geometry scale factor for the cooling tower fill material, Gfill. This value describes the size of the cooling tower. The block inverts the expression for the heat transfer conductance of the moist air side, UMAA, and calculates Gfill from the heat transfer conductance at nominal operating conditions. The block then uses Gfill to calculate the heat transfer conductance on the moist air side at actual operating conditions during simulation. The block does not model convective heat transfer in the thermal liquid film.
Gfill at nominal operating conditions is
where the subscript nom denotes the variable value at the specified nominal operating condition.
The block solves for (UMAA)nom with
The block calculates NTUnom by inverting the applicable effectiveness equation.
When Flow arrangement is Counter
flow,
where CRnom is the capacity ratio and with Qcombined, Qcombined,max, and CRnom evaluated at the nominal operating conditions.
When Flow arrangement is Cross
flow and the fluid with the lower value for C
is mixed
If the fluid with the lower value for C is unmixed,
Thermal Liquid Equations
The pressure of the thermal liquid when it enters the cooling tower at port A1 is
where pMA is the moist air pressure inside the cooling tower. Because the block assumes that water loss due to evaporation is small, the thermal liquid mass flow rate is equal to the port A1 inflow rate, .
The steady state mass balance equation for the thermal liquid is
where:
λ is the value of the Drift rate as fraction of water flow parameter. The drift accounts for liquid droplets that blow out of the cooling tower without evaporating.
ṁTLfill,out is the mass flow rate of the thermal liquid at the exit point of the fill material.
The steady state mass balance equation for the thermal liquid is
where:
ΦTLA1 is the energy flow rate at port A1.
ΦTLfill,out is the energy flow rate out of the fill material.
If you select Model cold-water basin, the block models an internal tank with the tank outlet at the bottom of the tank. Because the water in the tank must be replenished, the thermal liquid mass and energy conservation equations have two additional source terms, ṁTLmakeup and ΦTLmakeup.
When you select Automatically replenish lost water,
where hTLmakeup is the thermal liquid specific enthalpy specified by the Temperature of make-up water parameter.
If you clear the Automatically replenish lost water check box, you can specify the volumetric flow rate and temperature of the tank make-up water with ports Vm and Tm, respectively. Port L outputs the liquid level in the basin. The make-up water terms are
where:
pMA is the moist air pressure in the cooling tower.
Tmu is the temperature of the make-up water, which is the value of the signal at port Tm.
ρTL(pMA,Tmu) is the thermal liquid density evaluated at the moist air pressure and make-up water temperature.
hTL(pMA,Tmu) is the thermal liquid specific enthalpy evaluated at the moist air pressure and make-up water temperature.
If you select Model cold-water basin, the block models an internal tank. ṁTLfill,out and ΦTLA1 define the input flows of the internal tank. Port B1 is the outlet of the internal tank.
If you clear the Model cold-water basin check box,
Port B1 acts as a flow rate source for any downstream components. Connect a Tank (TL) block to port B1 to model the cold water basin. The Inlet height parameter of the Tank (TL) block must be larger than the liquid level in the tank.
Moist Air Equations
The behavior of the moist air side of the block depends on the Moist air operating conditions parameter.
When you set Moist air operating conditions to
Provided by input signals, the block enables
physical signal ports that you can use to specify the moist air attributes:
Port P is the input signal for the moist air inlet pressure. The moist air pressure, pMA, is equal to the value of this signal.
Port T is the input signal for the moist air dry-bulb temperature.
The flow rate input port depends on the Flow rate input signal specification parameter:
Value of Flow rate input signal specification Enabled Port Port Meaning Mass flow rateM Moist air mixture mass flow rate Volumetric flow rateV Moist air mixture volumetric flow rate Fan powerPwr Moist air fan power The humidity level input port depends on the Humidity input signal specification parameter:
Value of Humidity input signal specification Enabled Port Port Meaning Relative humidityW Moist air inlet relative humidity Specific humidityW Moist air inlet specific humidity Mole fractionW Moist air inlet water vapor mole fraction Humidity ratioW Moist air inlet humidity ratio Wet-bulb temperatureTw Moist air inlet wet-bulb temperature When Flow rate input signal specification is
Mass flow rateorVolumetric flow rate, the block uses the signal at port M or V to calculate the moist air mixture mass flow rate that enters the cooling tower, ṁMAin. The dry air and trace gas flow rate isThe block calculates the humidity ratio, WMAin, from the input signals at ports P, T, and W or Tw.
When Flow rate input signal specification is
Fan power, the fan power, Φfan, is proportional to the cube of the volumetric flow rate, q, and pressure gain across the fan, Δp.The moist air mixture volumetric flow rate is
where:
Pwr is the value of the signal at port Pwr.
Φfannom is the value of the Nominal fan power parameter.
qMAnom is the nominal volumetric flow rate. If you select Specify full moist air nominal condition, qMAnom is the value of the Nominal moist air volumetric flow rate parameter. If you clear Specify full moist air nominal condition, the block calculates qMAnom from the nominal water flow rate so that the capacity ratio is one.
When Moist air operating conditions is
Provided by input signals, the block does not
model trace gas.
When you set Moist air operating conditions to
Moist air domain ports, the block enables the
moist air ports A2 and B2, which you
can connect to a moist air network. Because the direction of the moist air flow
does not matter in this block, either port A2 or
B2 can be the inlet. The dry air and trace gas flow
rate is
where:
ṁMAin is the moist air mixture mass flow rate at port A2 or B2.
WMAin is the moist air mixture humidity ratio at port A2 or B2.
The moist air mixture mass conservation equation is
where:
ṁMAA2 and ṁMAB2 are the mass flow rates at ports A2 and B2.
MMA is the total mixture mass of the moist air volume.
The water vapor mass conservation equation is
where xwMA is the specific humidity of the moist air volume and ṁwMAA2 and ṁwMAB2 are the water vapor mass flow rates at ports A2 and B2.
The trace gas mass conservation equation is
where xgMA is the trace gas mass fraction of the moist air volume and ṁgMAA2 and ṁgMAB2 are the trace gas mass flow rates at ports A2 and B2.
The water droplet mass conservation equation is
where:
rdMA is the mass ratio of the water droplets to the moist air.
ṁdMAA2 and ṁdMAB2 are the water droplet mass flow rates at ports A2 and B2.
The moist air mixture energy conservation equation is
where uMA is the mixture specific internal energy of the moist air volume and ΦMAA2 and ΦMAB2 are the moist air mixture energy flow rates at ports A2 and B2.
The pressure loss of the moist air in the cooling tower is
where:
ΔpMAnom is the value of the Nominal moist air pressure loss parameter.
qMAnom is the value of the Nominal moist air volumetric flow rate parameter.
qMA is the volumetric flow rate of moist air through the cooling tower.
Using the Cooling Tower in a Model
When using the Cooling Tower (TL-MA), follow these guidelines:
If you clear the Model cold-water basin check box, you must connect the cooling tower port B1 to a Tank (TL) block.
When modeling transient situations such as startup or shutdown, connect the cooling tower port A1 to port A of a Partially Filled Pipe (TL) block to avoid a possible nonphysical situation of liquid flowing out of port A1. During startup and shutdown, port A1 may be exposed to the environment, which means there is no liquid present. The partially-filled pipe handles this scenario by allowing the liquid level to fall along the pipe while port A1 is exposed, if necessary.
Some cooling towers may use a pressure source to force water out of the spray nozzles and spread the water over a wider area, which causes a pressure drop at the inlet. To model pressure drop through the spray nozzles, connect a block that models pressure loss, such as an Orifice (TL), Local Resistance (TL), or Flow Resistance (TL) block, to port A1 of the cooling tower.
The Cooling Tower (TL-MA) block models a direct-contact cooling tower. To model an indirect-contact cooling tower, connect the thermal liquid side of the Cooling Tower (TL-MA) block to one side of a Heat Exchanger (TL-TL) block. In this configuration, the other side of the heat exchanger block represents the thermal liquid flowing into and out of the cooling tower, and the block models the heat transfer from the coil inside the cooling tower.
If you set Moist air operating conditions to
Moist air domain ports, you can model a mechanical forced-draft or an induced-draft cooling tower. To model a forced-draft cooling tower, connect a Fan (MA) block to the moist air inlet side of the tower. To model an induced-draft cooling tower, connect a Fan (MA) block to the moist air outlet side. If you set Moist air operating conditions toProvided by input signals, the block does not distinguish between forced-draft or induced-draft cooling towers.
Assumptions and Limitations
The block only models a mechanical-draft cooling tower, which means a fan moves the moist air through the tower.
The block only models a direct-contact cooling tower, which means the thermal liquid is in direct contact with the moist air.
Examples
Ports
Input
Output
Conserving
Parameters
References
[1] Mitchell JW, Braun JE. Principles of heating, ventilation, and air conditioning in buildings. Hoboken: Wiley, 2013.
[2] ASHRAE Standard Committee. 2012 ASHRAE Handbook—HVAC Systems and Equipment (SI). 2012.
[3] ASHRAE Standard Committee. 2013 ASHRAE Handbook—Fundamentals (SI). 2013.

