残差分析

残差のプロットと解析

近似モデルの残差は、各予測子値における応答データと応答データの近似の差として定義されます。

"残差" = "データ" – "近似"

曲線フィッター アプリで残差を表示するには、[曲線フィッター] タブの [可視化] セクションにある [残差プロット] をクリックします。

数学的に、特定の予測子値の残差は応答値 y と予測された応答値 ŷ の差です。

r = y – ŷ

データに当てはめるモデルが正しいと仮定すると、残差は確率的誤差に近づきます。そのため、残差がランダムに振る舞っているように見える場合、モデルがデータを適切に近似していることを示しています。一方、残差が体系的なパターンを示している場合、それはモデルがデータを適切に近似していないという明白な印です。モデルがデータに対して著しく不適切な場合、信頼限界など、モデル近似の多くの結果は無効であることを常に忘れないでください。

1 次多項式近似の残差のグラフ表示を次に示します。上のプロットは、データ点から近似曲線までの垂直距離として残差が計算されることを示しています。下の図は、近似 (0 のライン) に対する残差を示しています。

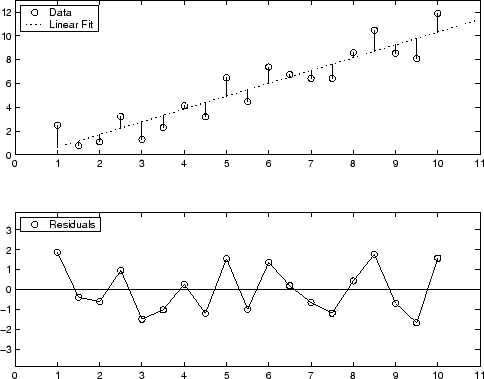
残差はゼロの周りでランダムに散在しているように見え、モデルがデータを適切に説明していることを示しています。

2 次多項式近似の残差のグラフ表示を次に示します。このモデルは、2 次の項のみを含み、線形項と定数項を含みません。

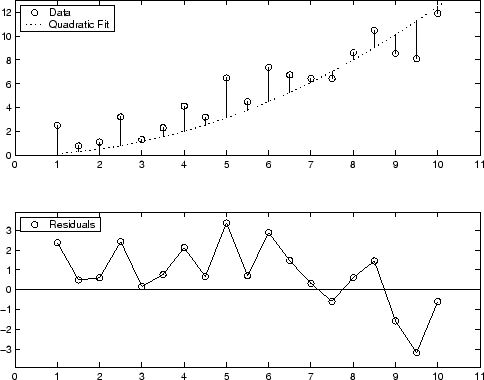
データ範囲の大部分で残差は体系的に正であり、このモデルがこのデータについて適切な近似ではないことを示しています。

例: 残差分析

この例では、いくつかの多項式モデルを使用して生成データを近似し、これらのモデルがどれだけ適切にデータを近似しているか、どれだけ正確に予測できるか評価します。データは 3 次曲線から生成されたもので、変数 x の範囲内にデータが存在しない大きな隙間があります。

x = [1:0.1:3 9:0.1:10]';
c = [2.5 -0.5 1.3 -0.1]; 
y = c(1) + c(2)*x + c(3)*x.^2 + c(4)*x.^3 + (rand(size(x))-0.5);

曲線フィッター アプリで 3 次多項式と 5 次多項式を使用してデータに当てはめます。データ、近似および残差を以下に示します。曲線フィッター アプリで残差を表示するには、[曲線フィッター] タブの [可視化] セクションにある [残差プロット] をクリックします。

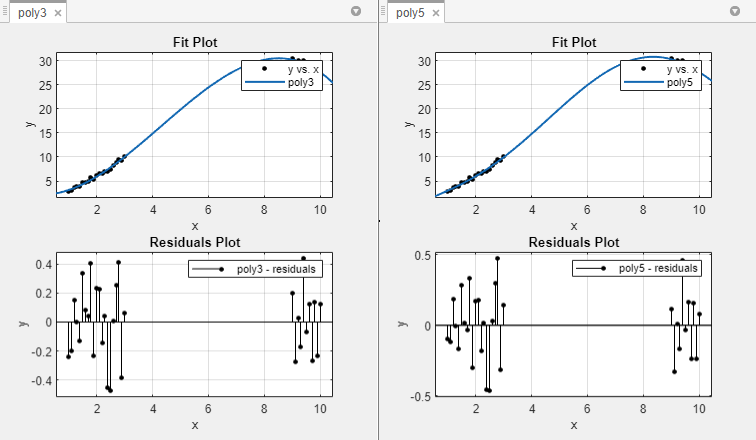
どちらのモデルもデータによく一致し、残差はゼロの周りでランダムに分布しているように見えます。そのため、これらの近似のグラフィカルな評価では、2 つの方程式の違いがはっきりとはわかりません。

[結果] ペインで数値的な近似結果を確認し、係数の信頼限界を比較します。

この結果は、3 次近似の係数は正確に求められている (範囲が小さい) が、5 次近似の係数は正確に求められていないことを示しています。生成データは 3 次曲線に従うため、予想どおり poly3 の近似結果が妥当です。近似係数の 95% 信頼限界は、許容できる範囲で係数が正確であることを示しています。一方、poly5 の 95% 信頼限界は、近似係数が正確に求められていないことを示しています。

適合度の統計量は [近似テーブル] ペインに表示されます。既定の設定では、自由度調整済み決定係数と RMSE の統計量がテーブルに表示されます。これらの統計量では、2 つの方程式の実質的な違いがわかりません。統計量の表示または非表示を選択するには、列ヘッダーを右クリックします。

新しい観測値の 95% 非同時予測限界を次に示します。曲線フィッター アプリで予測範囲を表示するには、[曲線フィッター] タブの [可視化] セクションにある [予測範囲] リストから [95%] を選択します。

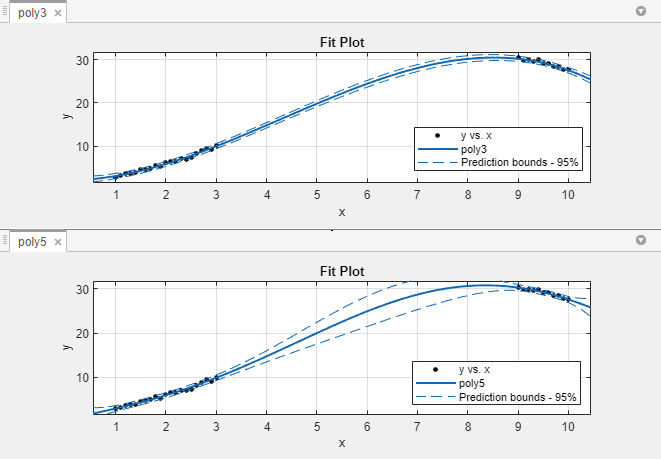
poly3 の予測限界は、データ範囲全体において小さな不確定性で新しい観測値を予測できることを示しています。poly5 の場合はそうではありません。データが存在しない領域で予測限界が広くなっています。これは明らかに、高次多項式項を正確に推定できるだけの十分な情報がデータに含まれていないためです。つまり、5 次多項式はデータに過適合しています。

poly5 を使用した近似関数の 95% 予測限界を次に示します。これでわかるように、関数の予測の不確定性がデータの中央で大きくなります。そのため、5 次多項式を使用して正確に予測するには、より多くのデータを収集しなければならないと結論づけることになります。

結論として、目的に最適な近似であると判断する前に、使用できる適合度による方法をすべて検証する必要があります。最初のアプローチとして必ず、近似と残差をグラフィカルに検証してください。ただし、一部の近似特性は数値的な近似結果、統計量および予測限界からのみ明らかになります。