Main Content

近似の微分と積分

スクリプトを開く

この例では、予測子値について近似の 1 階および 2 階微分を求め、更にその近似の積分を求める方法を示します。

ベースラインの正弦波信号を作成します。

xdata = (0:.1:2*pi)';
y0 = sin(xdata);

信号にノイズを追加します。

noise = 2*y0.*randn(size(y0)); % Response-dependent noise
ydata = y0 + noise;

ノイズを含むデータにカスタムの正弦波モデルを当てはめます。

f = fittype('a*sin(b*x)');
fit1 = fit(xdata,ydata,f,'StartPoint',[1 1]);

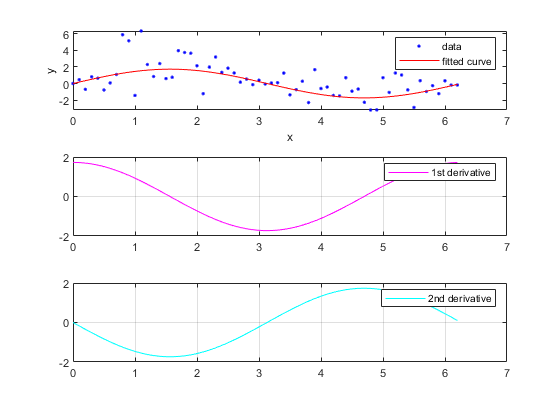
予測子値について近似の微分を求めます。

[d1,d2] = differentiate(fit1,xdata);

データ、近似、微分をプロットします。

subplot(3,1,1)
plot(fit1,xdata,ydata) % cfit plot method
subplot(3,1,2)
plot(xdata,d1,'m') % double plot method
grid on
legend('1st derivative')
subplot(3,1,3)
plot(xdata,d2,'c') % double plot method
grid on
legend('2nd derivative')

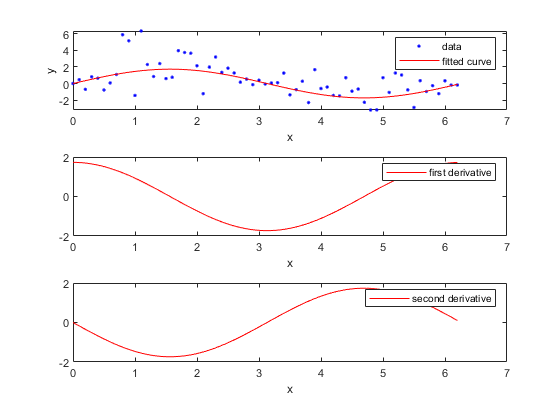
また、次のように cfit の plot メソッドを使用して微分を直接計算しプロットできることに注意してください。ただし、plot メソッドは微分データを返しません。

plot(fit1,xdata,ydata,{'fit','deriv1','deriv2'})

予測子値について近似の積分を求めます。

int = integrate(fit1,xdata,0);

データ、近似、積分をプロットします。

subplot(2,1,1)
plot(fit1,xdata,ydata) % cfit plot method
subplot(2,1,2)
plot(xdata,int,'m') % double plot method
grid on
legend('integral')

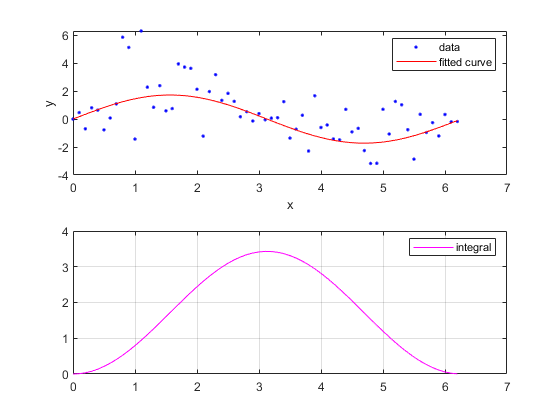
また、次のように cfit の plot メソッドを使用して積分を直接計算しプロットできることに注意してください。ただし、plot メソッドは積分のデータを返しません。

plot(fit1,xdata,ydata,{'fit','integral'})