近似のプログラムによる比較
この例では、Curve Fitting Toolbox™ を使用して 6 次までの多項式による国勢調査データへの近似および比較方法を示します。また、単項指数方程式で近似し、多項式モデルと比較する方法も説明します。
その手順では、以下を実行する方法を示します。
データを読み込み、異なるライブラリ モデルを使用して近似を作成。
グラフィカルな近似結果の比較と、近似係数および適合度の統計量を含む数値的な近似結果の比較により、最適な近似を探索。
データの読み込みとプロット
この例のデータはファイル census.mat です。
load census
ワークスペースには次の 2 つの新しい変数が含まれています。
cdate は、1790 年から 1990 年までの 10 年ごとの年度を示す列ベクトルです。
pop は、cdate の年度に対応する米国の人口数が記された列ベクトルです。
whos cdate pop plot(cdate,pop,'o')
Name Size Bytes Class Attributes cdate 21x1 168 double pop 21x1 168 double

2 次多項式の作成とプロット
関数 fit を使用して、多項式でデータを近似します。'poly2' を使用して 2 次多項式を指定します。fit の最初の出力は多項式で、2 番目の出力 gof には、後の手順で調べる適合度の統計量が含まれます。
[population2,gof] = fit(cdate,pop,'poly2');
近似をプロットするには plot メソッドを使用します。
plot(population2,cdate,pop); % Move the legend to the top left corner. legend('Location','NorthWest');

一連の多項式の作成とプロット
さまざまな次数の多項式を当てはめるには、たとえば 3 次多項式用に 'poly3' を使用して fittype を変更します。入力 cdate のスケールはかなり大きいため、データをセンタリングおよびスケーリングすると、より適切な結果が得られます。これを行うには、'Normalize' オプションを使用します。
population3 = fit(cdate,pop,'poly3','Normalize','on'); population4 = fit(cdate,pop,'poly4','Normalize','on'); population5 = fit(cdate,pop,'poly5','Normalize','on'); population6 = fit(cdate,pop,'poly6','Normalize','on');
人口増加の簡単なモデルから、指数方程式がこの国勢調査データによく合うだろうということがわかります。単項指数モデルで近似するには、fittype として 'exp1' を使用します。
populationExp = fit(cdate,pop,'exp1');
すべての近似を一度にプロットし、プロットの左上隅に意味のある凡例を追加します。
hold on plot(population3,'b'); plot(population4,'g'); plot(population5,'m'); plot(population6,'b--'); plot(populationExp,'r--'); hold off legend('cdate v pop','poly2','poly3','poly4','poly5','poly6','exp1',... 'Location','NorthWest');

残差のプロットによる近似の評価
残差をプロットするには、plot メソッドにプロット タイプとして 'residuals' を指定します。
plot(population2,cdate,pop,'residuals');

多項方程式の近似と残差はどれも似ているため、最適なものを選択することが難しくなっています。残差が体系的なパターンを示している場合、それはモデルがデータを適切に近似していないという明白な印です。
plot(populationExp,cdate,pop,'residuals');

単項指数方程式の近似と残差は、全体的に近似が適切でないことを示しています。したがって、これは不適切な選択であり、最適な近似の候補から指数近似を削除できます。
データ範囲外の近似の検証
2050 年までの近似の振る舞いを検証します。国勢調査データの近似の目標は、最適な近似を外挿して将来の人口値を予測することです。既定の設定では、近似はデータの範囲全体についてプロットされます。別の範囲で近似をプロットするには、近似をプロットする前に x 軸範囲を設定します。たとえば、近似から外挿された値を確認するには、x 軸範囲の上限を 2050 に設定します。
plot(cdate,pop,'o'); xlim([1900, 2050]); hold on plot(population6); hold off
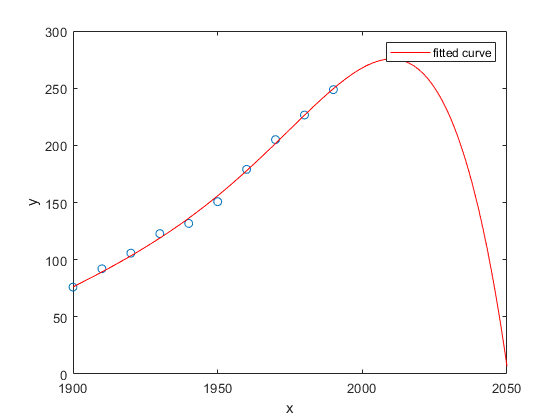
プロットを検証します。データ範囲外での 6 次多項式近似の振る舞いから、これは外挿に適した選択ではないため、この近似は棄却できます。
予測区間のプロット
予測区間をプロットするには、プロット タイプとして 'predobs' または 'predfun' を使用します。たとえば、2050 年までの新しい観測値について 5 次多項式の予測限界を確認するには次のようにします。
plot(cdate,pop,'o'); xlim([1900, 2050]) hold on plot(population5,'predobs'); hold off

3 次多項式の予測区間を 2050 年までプロットします。
plot(cdate,pop,'o'); xlim([1900, 2050]) hold on plot(population3,'predobs') hold off

適合度の統計量の検証
struct gof は近似 'poly2' の適合度の統計量を示します。前述の手順で関数 fit を使用して近似 'poly2' を作成したとき、gof 出力引数を指定しました。
gof
gof =
struct with fields:
sse: 159.0293
rsquare: 0.9987
dfe: 18
adjrsquare: 0.9986
rmse: 2.9724
誤差の二乗和 (SSE) と自由度調整済み決定係数の統計量を検証すると、最適な近似の決定に役立ちます。SSE の統計量は近似の最小二乗誤差であり、値がゼロに近いほど近似が適切であることを示します。一般に、自由度調整済み決定係数の統計量は、係数をモデルに追加するときに近似品質の最も優れた指標になります。
'exp1' の大きな SSE は、この近似が適切でないことを示しています。これについては、近似と残差の検証により既に判断済みです。SSE 値が最小なのは 'poly6' です。ただし、データ範囲外でのこの近似の振る舞いから、これは外挿に適した選択ではありません。新しい軸の範囲を使用したプロットの検証により、この近似は棄却済みです。
その次に SSE 値が適切なのは 5 次多項式近似 'poly5' であり、これが最適な近似である可能性があります。ただし、残りの多項式近似の SSE と自由度調整済み決定係数の値はすべて互いに非常に近い値です。どれを選択したら良いでしょうか。
係数および信頼限界の比較による適切な近似の決定
最適な近似の問題を解決するために、残りの近似である 5 次多項式と 2 次多項式の係数と信頼限界を検証します。
モデル、近似係数、近似係数の信頼限界を表示して、population2 と population5 を検証します。
population2 population5
population2 =
Linear model Poly2:
population2(x) = p1*x^2 + p2*x + p3
Coefficients (with 95% confidence bounds):
p1 = 0.006541 (0.006124, 0.006958)
p2 = -23.51 (-25.09, -21.93)
p3 = 2.113e+04 (1.964e+04, 2.262e+04)
population5 =
Linear model Poly5:
population5(x) = p1*x^5 + p2*x^4 + p3*x^3 + p4*x^2 + p5*x + p6
where x is normalized by mean 1890 and std 62.05
Coefficients (with 95% confidence bounds):
p1 = 0.5877 (-2.305, 3.48)
p2 = 0.7047 (-1.684, 3.094)
p3 = -0.9193 (-10.19, 8.356)
p4 = 23.47 (17.42, 29.52)
p5 = 74.97 (68.37, 81.57)
p6 = 62.23 (59.51, 64.95)
confint を使用して信頼区間を取得することもできます。
ci = confint(population5)
ci =
-2.3046 -1.6841 -10.1943 17.4213 68.3655 59.5102
3.4801 3.0936 8.3558 29.5199 81.5696 64.9469
係数の信頼限界によって係数の精度が決まります。近似方程式 (f(x)=p1*x+p2*x... など) を確認し、各係数のモデル項を調べます。p2 は 'poly2' の項 p2*x と 'poly5' の項 p2*x^4 を示していることに注意してください。正規化した係数と正規化していない係数を直接比較しないでください。
5 次多項式の係数 p1、p2 および p3 については、範囲がゼロと交差します。そのため、これらの係数がゼロではないという確信はもてません。高次数のモデル項の係数がゼロになる場合、それらの項は近似に寄与しておらず、このモデルが国勢調査データに過適合していることを示しています。
定数項、1 次および 2 次の項に関連する近似係数は正規化されたどの多項方程式でもほぼ同一です。ただし、多項式の次数が大きくなると、高次の項に関連する係数範囲がゼロと交差し、過適合の可能性があることがわかります。
一方、2 次近似では p1、p2 および p3 の信頼限界が小さくゼロと交差しないため、近似係数がかなり正確に求められたことを示しています。
こうして、グラフィカルな近似結果と数値的な近似結果の両方を検証すると、国勢調査データを外挿するための最適な近似として 2 次多項式の population2 を選択することになります。
新しいクエリ点での最適な近似の評価
この国勢調査データを外挿するための最適な近似 population2 を選択しました。ここで、いくつかの新しいクエリ点で近似を評価してみます。
cdateFuture = (2000:10:2020).'; popFuture = population2(cdateFuture)
popFuture = 274.6221 301.8240 330.3341
将来の人口の予測について 95% 信頼限界を計算するために、predint メソッドを使用します。
ci = predint(population2,cdateFuture,0.95,'observation')
ci = 266.9185 282.3257 293.5673 310.0807 321.3979 339.2702
近似とデータに対して、予測された将来の人口を信頼区間と共にプロットします。
plot(cdate,pop,'o'); xlim([1900, 2040]) hold on plot(population2) h = errorbar(cdateFuture,popFuture,popFuture-ci(:,1),ci(:,2)-popFuture,'.'); hold off legend('cdate v pop','poly2','prediction','Location','NorthWest')
