このページは機械翻訳を使用して翻訳されました。最新版の英語を参照するには、ここをクリックします。

固定翼物体による航空機設計の最適化

この例では次を使用します。

ライブスクリプトを開く

この例では、Aero.FixedWing オブジェクトを使用して航空機のサイズと形状を最適化し、静的安定性制約を適用する方法を示します。

航空機設計目標

この航空機は、自動車技術協会 (SAE) の航空設計コンペティションのレギュラークラス向けに設計されています。この競技では、チームは以下のように計算される飛行スコアの最大化を目指します。

$F S = 3 \frac{2 N_{S} + 2.2 W_{B P}}{b_{w} + l_{c a r g o}}$

ここで、

$N_{s} :$ 球状ペイロードの数

$W_{B P} :$ 梱包された積荷の重量 [kg]

$b_{W} :$ 翼幅 [m]

$l_{c a r g o} :$ 貨物室の長さ [m]

これらすべての変数は、離散的な $N_{s}$ を除いて、基本的に連続しています。この変数は問題の定式化を複雑にします。したがって、 $N_{s} = 1$ の場合のみが考慮されます。

最適化制約

競争は最適化にとって重要な制約を課します。

総離陸重量は24.9kgを超えることはできません。
翼幅は3mを超えることはできません。
離陸距離は30.5mを超えることはできません。

これに加えて、従来の設計を優先するための追加要件を課します。

航空機は静的に安定していなければなりません。
翼、尾翼、ペイロード、航空電子機器、着陸装置間の干渉は許可されません。
プラントルの揚力線理論が有効であるためには、翼と水平尾翼のアスペクト比が十分に高くなければなりません。
翼と尾翼のアスペクト比は、構造強度を保証するために十分に低くなければなりません。
翼の空力中心は胴体の前半部になければなりません。
静的マージンを制限することで、航空機が外乱に過度に敏感にならずに容易にピッチングできるようにする必要があります。

さらに、すべての最適化変数は物理量であり、正の値でなければなりません。

仮定

定式化をさらに簡略化するために、翼が次のような単純な形状であると仮定します。

二面角なし
スイープなし
翼のねじれなし
翼端装置なし
$0 °$ 入射角
胴体中心線上の翼のZ位置

この設計では、操縦翼面や推進システムの影響も排除されています。

最適化問題の定式化

航空機の形状を最適化するには、問題ベースのアプローチを使用します。まず、この例に含まれているヘルパー関数 initializeAircraft を使用して、問題の定数と最適化変数を定義します。これらの変数を 6 つの構造 (aircraft、wing、hTail、vTail、fuselage、payload) に整理します。最適化変数とその物理的な表現のリストを以下で参照してください。

[aircraft, wing, fuselage, hTail, vTail, payload, initialValues] = initializeAircraft;

設計最適化問題を設定する

空の最適化問題を定義し、その目的として最大化を設定します。

designprob = optimproblem('ObjectiveSense','maximize');

翼、尾翼、胴体の揚力係数と抗力係数を推定します。

[aircraft, wing, fuselage, hTail, vTail, designprob] = ...
    addAerodynamics(aircraft, wing, fuselage, hTail, vTail, designprob);

コンポーネント構築法を使用して航空機の質量を定式化し、総離陸重量の制約を導入します。

[aircraft, wing, fuselage, hTail, vTail, payload, designprob] = ... 
    addWeightAndSizing(aircraft, wing, fuselage, hTail, vTail, payload, designprob);

静的安定性導関数を計算するには、Aero.FixedWing および Aero.FixedWing.State オブジェクトのインスタンスを作成します。

[myAircraft, CruiseState] = createFixedWing(aircraft.Mass, wing, hTail, initialValues);

最適化問題に静的安定性制約を追加します。次の 10 個の導関数は、外部擾乱に対する航空機の応答において重要な役割を果たすため、制約として使用されます: $C_{D_{u}}$ 、 $C_{m_{u}}$ 、 $C_{Y_{v}}$ 、 $C_{L_{w}}$ 、 $C_{m_{α}}$ 、 $C_{l_{β}}$ 、 $C_{n_{β}}$ 、 $C_{l_{p}}$ 、 $C_{m_{q}}$ 、 $C_{n_{r}}$ 。

これらの導関数を計算するために、addStability 関数は航空機のすべての空力係数と質量慣性モーメント行列を計算します。この情報を使用して、Aero.FixedWing オブジェクトの staticStability メソッドを使用して 10 個の安定性導関数を取得します。

[aircraft, wing, vTail, designprob] = ...
    addStability(aircraft, wing, fuselage, hTail, vTail, payload, designprob, myAircraft, CruiseState);

離陸性能を推定し、最大離陸距離または地上滑走の制約を含めます。

[aircraft,designprob] = addPerformance(aircraft, wing.PlanformArea, wing.MeanChord, designprob);

SAE Aero Design Regular Class 飛行スコアに一致する目的関数を記述します。単位はメートル法に変換されます。

designprob.Objective = 3*(2+2.2*payload.Boxed.Mass)/((2*wing.HalfSpan+payload.Length));

最適化ソルバーのオプションを設定する

関数評価と反復の最大回数を無限に設定して、ソルバーを完了まで実行します。

options = optimoptions(designprob);
options.MaxFunctionEvaluations = Inf;
options.MaxIterations = Inf;

ステップが小さくなりすぎる場合は、最適化を早期に停止します。

options.StepTolerance = 1e-4;

ソルバーが実行中に各反復の結果を自動的にプロットするようにします。

options.PlotFcn = {'optimplotconstrviolation', 'optimplotfvalconstr'};

並列プールを使用して計算を高速化します。

options.UseParallel = true;
options.Display = 'off';

最適化問題を解く

問題を解くと、この設計の最大飛行スコアと、12 個の最適化変数の対応する値の両方が返されます。

[finalValues, maxScore] = solve(designprob, initialValues, 'Options', options);

Starting parallel pool (parpool) using the 'Processes' profile ...
Connected to parallel pool with 4 workers.

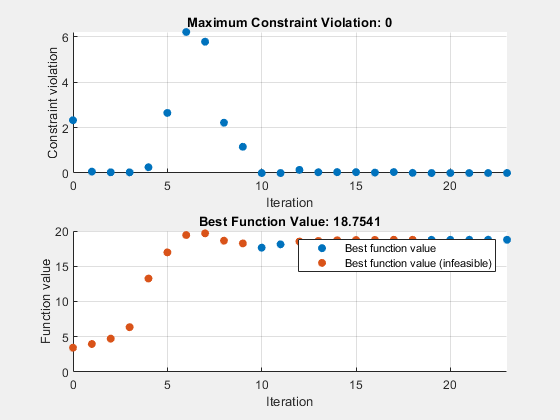
maxScore

maxScore = 18.7541

ソリューションはすぐに最適値に近づき、ほとんどのステップは最終的な改善に費やされます。この問題の非線形性のため、解決策は全体的に最適ではない可能性があります。初期条件が異なると、予測される飛行スコアが 18.754 より高くなる可能性があります。最適化された設計では、大きなテーパード翼と胴体の端に配置された適度な大きさの尾翼を備えた最終的な形状になります。

参考文献

[1] Roskam、1 月 Airplane Design、パート VI:空力特性、推力特性、出力特性の予備計算。ローレンス、カンザス州:DARコーポレーション、2008年。

[2] ロスカム、ヤン。飛行機の飛行力学と自動飛行制御、パートI。ローレンス、KA：DARコーポレーション、2003年。

[3] レイマー、ダニエル P. 航空機設計:概念的なアプローチ。ワシントンDC：AIAA、1992年。

参考

Aero.FixedWing | Aero.FixedWing.State