このページは機械翻訳を使用して翻訳されました。最新版の英語を参照するには、ここをクリックします。

Orbit Propagator ブロックによる月面ミッションの分析

この例では次を使用します。

この例では、アポロコマンドおよびサービスモジュールと月面上のローバー間のアクセス間隔を計算して視覚化する方法を示します。モジュールの軌道は、NASAの報告書「アポロCSMモジュールの月軌道パラメータの変動」[2]の参照軌道#2を使用してモデル化されています。これはNASAがアポロ計画のために研究した月の軌道です。例では以下を使用します:

Aerospace Toolbox
Aerospace Blockset™
Mapping Toolbox™

ミッションパラメータとモジュールの初期条件を定義する

ミッションの開始日と期間を指定します。この例では、MATLAB ® 構造を使用してミッションデータを整理します。これらの構造により、例の後半でのデータへのアクセスがより直感的になります。また、グローバルベースワークスペースの整理にも役立ちます。

mission.StartDate = datetime(1969, 9, 20, 5, 10, 12.176);
mission.Duration  = hours(2);

基準軌道#2 [2]に基づいて、mission.StartDateにおけるコマンドおよびサービスモジュール（CSM）のケプラー軌道要素を指定します。参考資料 2 に記載されている参照軌道の基準は次のとおりです。

軌道面には、月面の地球側にある着陸地点のベクトルが含まれていなければならない。その着陸地点のベクトルは、月面座標で経度315度から45度、緯度+5度から-5度の範囲にある。[2]
軌道面は、月面投入後3時間から39時間の間に月着陸側が軌道面から0.5度以上外れないように向けられなければならない。[2]

csm.SemiMajorAxis  = 1894578.3;     % [m]
csm.Eccentricity   = 0.0004197061;
csm.Inclination    = 155.804726;    % [deg]
csm.RAAN           = 182.414087;    % [deg]
csm.ArgOfPeriapsis = 262.877900;    % [deg]
csm.TrueAnomaly    = 0.000824;      % [deg]

傾斜角度は ICRF X-Y 平面に対する相対角度であることに注意してください。ICRF の X-Y 軸は地球の北極に対して垂直です。黄道に対する地球の軸の傾きは約 23.44 度ですが、月の軸の傾きは約 5.145 度です。したがって、ICRF X-Y 平面に対する月の軸の傾きは、およそ $23.44 \pm 5.145$ 度の間で変化します。これは、上記の約 155.8 度の軌道傾斜角が、月面座標で $\pm 5$ 度の緯度を維持するという要件を満たす理由を説明しています。

視線アクセス解析で使用する月面上のローバーの緯度と経度を指定します。

rover.Latitude  =0;  % [deg]
rover.Longitude =23.5; % [deg]

モデルを開いて構成する

付属のSimulink®モデルを開きます。このモデルには、出力ポートに接続された Orbit Propagator ブロックが含まれています。 Orbit Propagator ブロックはベクトル化をサポートします。これにより、ブロックパラメーター ウィンドウで初期条件の配列を指定するか、set_param を使用することで、1 つのブロックで複数の衛星をモデル化できます。

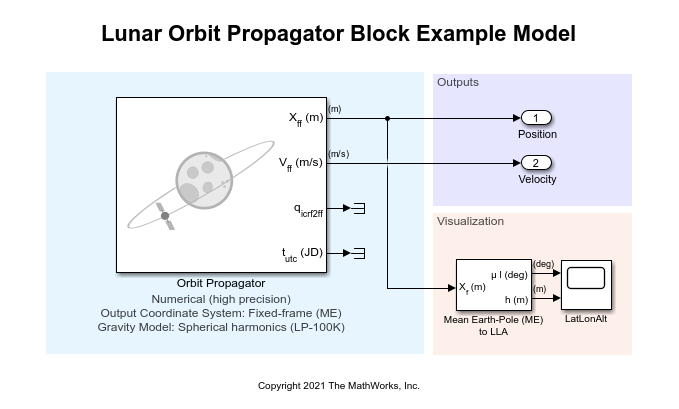
mission.mdl = "LunarOrbitPropagatorBlockExampleModel";
open_system(mission.mdl);

SimulationInput オブジェクトを使用して、ミッションのモデルを構成します。SimulationInput オブジェクトを使用すると、モデルを変更せずに複数のミッションを構成し、それらの設定でシミュレーションを実行できます。

mission.sim.in = Simulink.SimulationInput(mission.mdl);

モデル内の Orbit Propagator ブロックへのパスを定義します。

csm.blk = mission.mdl + "/Orbit Propagator";

ベースワークスペースに Moon プロパティを読み込みます。

moon.F = 0.0012;  % Moon ellipticity (flattening) (Ref 1)
moon.R_eq = 1737400; % [m] Lunar radius in meters (Ref 1)
moon.ReferenceEllipsoid = referenceEllipsoid("moon","meter"); % Moon reference ellipsoid
moon.Data = matfile("lunarGeographicalData.mat"); % Load moon geographical data

CSM の初期条件を設定します。前のセクションで定義したケプラーの軌道要素セットを割り当てるには、setBlockParameter を使用します。

mission.sim.in = mission.sim.in.setBlockParameter(...
    csm.blk, "startDate", string(juliandate(mission.StartDate)),...
    csm.blk, "stateFormatNum", "Orbital elements",...
    csm.blk, "orbitType", "Keplerian",...
    csm.blk, "semiMajorAxis", string(csm.SemiMajorAxis),...
    csm.blk, "eccentricity", string(csm.Eccentricity),...
    csm.blk, "inclination", string(csm.Inclination),...
    csm.blk, "raan", string(csm.RAAN),...
    csm.blk, "argPeriapsis", string(csm.ArgOfPeriapsis),...
    csm.blk, "trueAnomaly", string(csm.TrueAnomaly));

ブロックの位置と速度の出力ポートを、月固定フレームを使用するように設定します。月の固定フレームは、平均地球/極軸 (ME) 参照システムです。

mission.sim.in = mission.sim.in.setBlockParameter(...
    csm.blk, "centralBody", "Moon",...
    csm.blk, "outportFrame", "Fixed-frame");

プロパゲーターを構成します。

mission.sim.in = mission.sim.in.setBlockParameter(...
    csm.blk, "propagator", "Numerical (high precision)",...
    csm.blk, "gravityModel", "Spherical Harmonics",...
    csm.blk, "moonSH", "LP-100K",... % moon spherical harmonic potential model
    csm.blk, "shDegree", "100",... % Spherical harmonic model degree and order
    csm.blk, "useMoonLib", "off");

setModelParameter を使用してモデルレベルのソルバー設定を適用します。数値プロパゲーターを使用する場合、最高のパフォーマンスと精度を得るには、可変ステップソルバーを使用します。

mission.sim.in = mission.sim.in.setModelParameter(...
    SolverType="Variable-step",...
    SolverName="VariableStepAuto",...
    RelTol="1e-6",...
    AbsTol="1e-7",...
    StopTime=string(seconds(mission.Duration)));

モデル出力ポートデータをタイムテーブルオブジェクトのデータセットとして保存します。

mission.sim.in = mission.sim.in.setModelParameter(...
    SaveOutput="on",...
    OutputSaveName="yout",...
    SaveFormat="Dataset",...
    DatasetSignalFormat="timetable");

モデルを実行してCSMエフェメリスを収集する

上記で定義した SimulationInput オブジェクトを使用してモデルをシミュレートします。この例では、Orbit Propagator ブロックは、月を中心とした固定座標フレームで位置と速度の状態を出力するように設定されています。

mission.sim.out = sim(mission.sim.in);

モデル出力データ構造から位置と速度データを抽出します。

csm.TimetablePos = mission.sim.out.yout{1}.Values;
csm.TimetableVel = mission.sim.out.yout{2}.Values;

timetable オブジェクトでミッションの開始日を設定します。

csm.TimetablePos.Properties.StartTime = mission.StartDate;

プロセスシミュレーションデータ

月の赤道半径と平坦化を使用して、緯度、経度、高度を計算します。値は度とメートルで表示されます。

csm.MEPos = [csm.TimetablePos.Data(:,1) ...
    csm.TimetablePos.Data(:,2) csm.TimetablePos.Data(:,3)];
lla = ecef2lla(csm.MEPos, moon.F, moon.R_eq);
csm.LLA = timetable(csm.TimetablePos.Time, ...
    lla(:,1), lla(:,2), lla(:,3), ...
    VariableNames=["Lat", "Lon", "Alt"]);
clear lla;
disp(csm.LLA);

            Time               Lat         Lon         Alt    
    ____________________    _________    _______    __________

    20-Sep-1969 05:10:12      -2.3072     175.32    1.5639e+05
    20-Sep-1969 05:10:22      -2.3039     174.83    1.5639e+05
    20-Sep-1969 05:11:12      -2.2846     172.39    1.5639e+05
    20-Sep-1969 05:13:36      -2.2061     165.35    1.5639e+05
    20-Sep-1969 05:16:00      -2.0947     158.31     1.564e+05
    20-Sep-1969 05:18:24       -1.952     151.27    1.5641e+05
    20-Sep-1969 05:20:48      -1.7804     144.24    1.5641e+05
    20-Sep-1969 05:23:12      -1.5824     137.21    1.5642e+05
    20-Sep-1969 05:25:36      -1.3608     130.17    1.5641e+05
    20-Sep-1969 05:28:00       -1.119     123.14    1.5641e+05
    20-Sep-1969 05:30:24     -0.86057     116.11     1.564e+05
    20-Sep-1969 05:32:48     -0.58934     109.09     1.564e+05
    20-Sep-1969 05:35:12     -0.30942     102.06    1.5639e+05
    20-Sep-1969 05:37:36    -0.025001     95.032    1.5639e+05
    20-Sep-1969 05:40:00      0.25967     88.006     1.564e+05
    20-Sep-1969 05:42:24      0.54034     80.978     1.564e+05
    20-Sep-1969 05:44:48      0.81284     73.951    1.5641e+05
    20-Sep-1969 05:47:12       1.0732     66.923    1.5642e+05
    20-Sep-1969 05:49:36       1.3175     59.893    1.5643e+05
    20-Sep-1969 05:52:00       1.5422     52.863    1.5646e+05
    20-Sep-1969 05:54:24       1.7439     45.831    1.5649e+05
    20-Sep-1969 05:56:48       1.9194     38.797    1.5652e+05
    20-Sep-1969 05:59:12       2.0662     31.763    1.5656e+05
    20-Sep-1969 06:01:36       2.1821     24.728     1.566e+05
    20-Sep-1969 06:04:00       2.2652     17.691    1.5664e+05
    20-Sep-1969 06:06:24       2.3145     10.655    1.5668e+05
    20-Sep-1969 06:08:48       2.3291     3.6183    1.5673e+05
    20-Sep-1969 06:11:12        2.309     -3.418    1.5676e+05
    20-Sep-1969 06:13:36       2.2544    -10.454    1.5679e+05
    20-Sep-1969 06:16:00       2.1663    -17.489    1.5682e+05
    20-Sep-1969 06:18:24        2.046    -24.522    1.5683e+05
    20-Sep-1969 06:20:48       1.8953    -31.554    1.5685e+05
    20-Sep-1969 06:23:12       1.7163    -38.585    1.5686e+05
    20-Sep-1969 06:25:36       1.5116    -45.614    1.5686e+05
    20-Sep-1969 06:28:00       1.2844    -52.642    1.5686e+05
    20-Sep-1969 06:30:24       1.0381    -59.668    1.5686e+05
    20-Sep-1969 06:32:48      0.77625    -66.693    1.5685e+05
    20-Sep-1969 06:35:12      0.50273    -73.718    1.5684e+05
    20-Sep-1969 06:37:36      0.22159    -80.741    1.5683e+05
    20-Sep-1969 06:40:00    -0.062926    -87.765    1.5682e+05
    20-Sep-1969 06:42:24     -0.34651    -94.789     1.568e+05
    20-Sep-1969 06:44:48     -0.62489    -101.81    1.5677e+05
    20-Sep-1969 06:47:12     -0.89393    -108.84    1.5673e+05
    20-Sep-1969 06:49:36      -1.1497    -115.87    1.5669e+05
    20-Sep-1969 06:52:00      -1.3884    -122.89    1.5664e+05
    20-Sep-1969 06:54:24      -1.6064    -129.92     1.566e+05
    20-Sep-1969 06:56:48      -1.8006    -136.96    1.5656e+05
    20-Sep-1969 06:59:12      -1.9679    -143.99    1.5652e+05
    20-Sep-1969 07:01:36      -2.1058    -151.03    1.5647e+05
    20-Sep-1969 07:04:00       -2.212    -158.06    1.5641e+05
    20-Sep-1969 07:06:24      -2.2849     -165.1    1.5635e+05
    20-Sep-1969 07:08:48      -2.3235    -172.14     1.563e+05
    20-Sep-1969 07:10:12      -2.3299    -176.25    1.5626e+05

結果

3D 月面上の CSM 軌道を表示

figure; axis off; colormap gray; view(-5,23);
axesm("globe","Geoid", moon.ReferenceEllipsoid);
geoshow(moon.Data.moonalb20c, moon.Data.moonalb20cR, DisplayType="texturemap");
plot3(csm.MEPos(:,1), csm.MEPos(:,2), csm.MEPos(:,3),"r");

CSM 地上トレースとローバー位置の 2D 投影を表示

figure; colormap gray;
axesm(MapProjection="robinson");
geoshow(moon.Data.moonalb20c, moon.Data.moonalb20cR, DisplayType="texturemap");
plotm(csm.LLA.Lat, csm.LLA.Lon, Color="r");
plotm(rover.Latitude, rover.Longitude, "xy", LineWidth=3);

関心のある時点でのCSMの視野を表示

分析する対象時間 (TOI) を定義します。この例では、データセット内の 30 番目のサンプルを選択します。

csm.TOI.LLA = csm.LLA(30,:);

月の中心から測定された軌道衛星の視線 (LOS) 視野 (FOV) の角度半径を計算します。

csm.TOI.FOV.Lambda0 = acosd(moon.R_eq / (moon.R_eq + csm.TOI.LLA.Alt)); % [deg]
[csm.TOI.FOV.Lats, csm.TOI.FOV.Lons] = ...
    scircle1(csm.TOI.LLA.Lat, csm.TOI.LLA.Lon, csm.TOI.FOV.Lambda0);

TOI をプロットします。CSM の位置は緑色の十字で示され、LOS 視野は破線の円で示されます。

figure; colormap gray;
axesm(MapProjection="robinson");
geoshow(moon.Data.moonalb20c, moon.Data.moonalb20cR, DisplayType="texturemap");
plotm(csm.TOI.FOV.Lats, csm.TOI.FOV.Lons, "g--", LineWidth=1); % CSM visibility projected onto the map
plotm(csm.LLA.Lat, csm.LLA.Lon, Color="r");                    % CSM ground trace
plotm(csm.TOI.LLA.Lat, csm.TOI.LLA.Lon, "g+", MarkerSize=8);   % sub-CSM point
plotm(rover.Latitude, rover.Longitude, "xy", LineWidth=3);

ローバーからの CSM 視線可視性を表示

月が球体であると仮定してアクセス間隔を推定します。

lambda_all  = acosd(moon.R_eq ./ (moon.R_eq + csm.LLA.Alt)); % [deg] angular radius of CSM FOV measured from Moon center  
d = distance(csm.LLA.Lat, csm.LLA.Lon, ...
    rover.Latitude, rover.Longitude);                        % [deg] angular distance between sub-CSM point and rover
rover.Access.InView = csm.LLA(lambda_all - d > 0,:);         % timetable containing the in view data samples
rover.Access.InView.Time.Format = "HH:mm:ss";
clear lambda_all d;

軌道モジュールとローバー間のアクセス間隔をプロットします。

if height(rover.Access.InView) ~= 0
    % Look for breaks in the timestamps to identify pass starts
    rover.Access.StartIdx = [1, find(diff(rover.Access.InView.Time) > minutes(5))]; 
    rover.Access.StartTime = rover.Access.InView.Time(rover.Access.StartIdx);
    rover.Access.StopIdx = [rover.Access.StartIdx(2:end)-1, height(rover.Access.InView)];
    rover.Access.StopTime = rover.Access.InView.Time(rover.Access.StopIdx);
    rover.Access.Duration = rover.Access.StopTime - rover.Access.StartTime;
    % Show pass intervals in table
    rover.Access.IntervalTable = table(rover.Access.StartTime, rover.Access.StopTime, rover.Access.Duration, ...
        VariableNames=["Pass Start", "Pass End", "Duration"]); 
    disp(rover.Access.IntervalTable);
    disp(' ');
    % Set up figure window/plot
    figure; colormap gray;
    axesm(MapProjection="robinson")
    geoshow(moon.Data.moonalb20c, moon.Data.moonalb20cR, DisplayType="texturemap")
    title(join(["Passes Between", string(csm.LLA.Time(1)), ...
        "and", string(csm.LLA.Time(end))]));
    % Plot inView, rover, and CSM orbit
    plotm(rover.Access.InView.Lat, rover.Access.InView.Lon, "+g");
    plotm(rover.Latitude, rover.Longitude, "xy", LineWidth=3);
    plotm(csm.LLA.Lat, csm.LLA.Lon, Color="r");
    % Plot pass inteval
    rover.Access.EdgeIndices = rover.Access.InView(sort([rover.Access.StartIdx rover.Access.StopIdx]), :);
    for j = 1 : height(rover.Access.EdgeIndices)
        textm(rover.Access.EdgeIndices.Lat(j) + 10, ...
            rover.Access.EdgeIndices.Lon(j), ...
            string(rover.Access.EdgeIndices.Time(j)), Color="y", Rotation=30);
    end 
else
    disp("The CSM is not visible from the rover during the defined mission time.")
end

    Pass Start    Pass End    Duration
    __________    ________    ________

     05:54:24     06:08:48    00:14:24

参考文献

[1] ウィリアムズ、デビッド・R博士「月ファクトシート」、惑星ファクトシート、NSSDCA、NASAゴダード宇宙飛行センター、2020年1月13日、https://nssdc.gsfc.nasa.gov/planetary/factsheet/moonfact.html。

[2] タイマー、T.P.(NASA ミッション分析オフィス)「アポロ CSM モジュールの月軌道パラメータの変化」、NASA TM X-55460。メリーランド州グリーンベルト:ゴダード宇宙飛行センター、1966年2月。

参考

Orbit Propagator