フーリエ解析からウェーブレット解析へ

内積

フーリエおよびウェーブレットの両方の変換によって、信号および "解析" 関数の間の相似性を測定します。両方の変換では、この相似性の測定方法として "内積" と呼ばれる数学的なツールを使用します。2 つの変換は、解析関数の選択において異なります。これにより、2 つの変換が信号と抽出可能な情報の種類を表す方法が異なります。

相似性の測定方法としての内積の簡単な例として、平面上のベクトルの内積について考えます。次の MATLAB^® の例では、平面上の 3 つの単位ベクトル $$\{u,v,w\}$$ の内積を計算します。

$$\begin{array}{l}\{\left(\begin{array}{c}\sqrt{3}/2\\ 1/2\end{array}\right),\left(\begin{array}{c}1/\sqrt{2}\\ 1/\sqrt{2}\end{array}\right),\left(\begin{array}{c}0\\ 1\end{array}\right)\}\\ \end{array}$$

u = [sqrt(3)/2 1/2];
v = [1/sqrt(2) 1/sqrt(2)];
w = [0 1];
% Three unit vectors in the plane
quiver([0 0 0],[0 0 0],[u(1) v(1) w(1)],[u(2) v(2) w(2)]);
axis([-1 1 0 1]);
text(-0.020,0.9371,'w');
text(0.6382,0.6623,'v');
text(0.7995,0.4751,'u');
% Compute inner products and print results
fprintf('The inner product of u and v is %1.2f\n', dot(u,v))
fprintf('The inner product of v and w is %1.2f\n', dot(w,v))
fprintf('The inner product of u and w is %1.2f\n', dot(u,w))

図を見ると、u および v は、方向において最もよく似ていますが、u および w の相似性は最も低くなります。

内積は、この幾何学的な事実を捉えます。数学的に、2 つのベクトル u および v の内積は、それらの間の角度 θ のノルムおよび余弦の積と等しくなります。

$$\begin{array}{l}<u,v>=\left|\text{}\right|u\left|\right|\left|\right|v\left|\right|\cos (\theta )\\ \end{array}$$

u および v の両方に単位ノルム、または単位エネルギーを持つ特殊なケースの場合、内積は cos(θ) と等しくなり、したがって、[-1,1] の間に含まれます。この場合、内積を相関係数として直接解釈できます。u または v のいずれかに単位ノルムがない場合、内積は絶対値で 1 を超過する場合があります。ただし、それでも相関の一種として解釈可能にする 2 つのベクトル間の角度の余弦によって、内積は異なります。内積の絶対値は、それらの間の角度が 0 または $$\pi$$ ラジアン (0 または 180 度) である場合に、最も大きくなることに注意してください。これは、一方のベクトルが他方の実数値のスカラー倍である場合に発生します。

フーリエ変換およびウェーブレット変換で発生するような高次元空間の内積は、以前の例と同様の幾何学的解釈の容易さを示すことはありませんが、これらの相似性の測定方法は同じです。これらの変換の実用性で重要なのは、それらが基本的に、信号および周波数、スケール、位置などのある物理的な性質を持つ一部の基本関数の間の相関の概要を示すという部分です。これらの構成要素の信号の概要を示すことで、信号を生成したメカニズムをより良く理解できるようになります。

フーリエ変換

フーリエ解析は、ウェーブレット変換を導入するための開始点として、またウェーブレット解析がフーリエ解析よりもさらに役立つ信号の特性を与えるケースを示すためのベンチマークとして使用されます。

数学的に、フーリエ解析のプロセスは "フーリエ変換" によって表されます。

$$F(\omega )={\displaystyle {\int }_{-\infty }^{\infty }f}(t)e^{-j\omega t}dt.$$

これは、複素指数で乗算された信号 f(t) のすべての時間に対する積分 (合計) です。複素指数は実数部と虚数部の正弦波成分に分割できることを思い出してください。フーリエ変換は、単一変数の関数を別の単一変数の関数にマッピングすることに注意してください。

フーリエ変換を定義する積分が "内積" です。2 つの信号間の相似性の内積を測定する方法の例については、内積を参照してください。ω の各値について、時間のすべての値にわたる積分 (または合計) により、2 つの信号がどの程度類似しているかを要約するスカラー F(ω) を生成します。これらの複素数値は "フーリエ係数" です。概念的には、各フーリエ係数 F(ω) を周波数の複素指数 (正弦波) で乗算すると、元の信号の構成正弦波成分が生成されます。プロセスを図で表すと次のようになります。

$$e^{j\omega t}$$ が複素数値であるため、F(ω) は一般的に複素数値です。信号の $${\omega }_0$$ の角周波数上に大きな振動がある場合、$$F({\omega }_0)$$ の絶対値は大きくなります。$$|F(\omega )|$$ のプロットを角周波数の関数として調べることで、どの周波数が f(t) の変動性に最も寄与しているかを決定することが可能です。

フーリエ変換が異なる周波数の信号および正弦波の間の相似性を捉える方法を説明するために、次の MATLAB コードでは、加法性ノイズによって破損した 4 および 8 Hz の 2 つの正弦波から構成される信号を、離散フーリエ変換を使用して解析します。

rng(0,'twister');
Fs = 128;
t = linspace(0,1,128);
x = 2*cos(2*pi*4*t)+1.5*sin(2*pi*8*t)+randn(size(t));
xDFT = fft(x);
Freq = 0:64;
subplot(211);
plot(t,x); xlabel('Seconds'); ylabel('Amplitude');
subplot(212);
plot(Freq,abs(xDFT(1:length(xDFT)/2+1)))
set(gca,'xtick',[4:4:64]);
xlabel('Hz'); ylabel('Magnitude');

時間信号として見た場合、データ内にどのような大きな振幅があるかを決定するのは困難です。ただし、フーリエ変換係数の絶対値を周波数の関数として見ると、4 および 8 Hz の主要な振動が容易に検出されます。

短時間フーリエ変換

フーリエ変換は、信号および単一複素数を持つ正弦波の間の相似性の概要を示します。複素数の大きさは、特定の周波数のどの振動が信号のエネルギーに寄与するかを捉える一方で、複素数の引数が位相情報を捉えます。フーリエ係数には時間依存性がないことに注意してください。フーリエ係数は、すべての時間に対する統合および合計によって求められます。そのため、この情報が失われていることが明確です。以下の 2 つの信号について考えます。

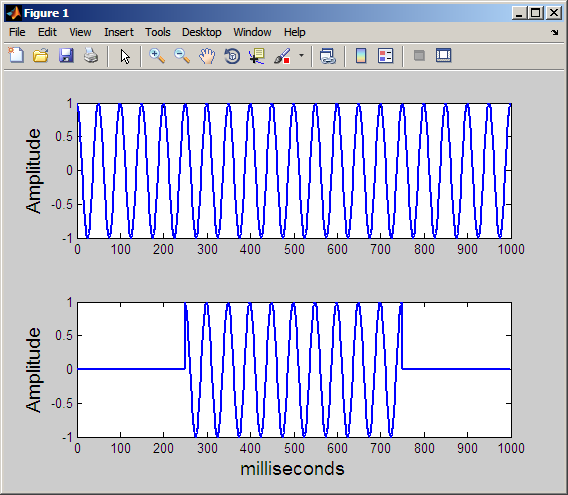
信号は、両方とも周波数 20 Hz の単一の正弦波から構成されます。ただし、上の信号では、正弦波は 1000 ミリ秒継続します。下のプロットでは、正弦波は 250 ミリ秒時点で開始し、750 ミリ秒で終了します。フーリエ変換によって 2 つの信号が同じ周波数成分を持つことが検出されますが、フーリエ変換には 20 Hz の振動の持続時間が 2 つの信号間で異なることを把握する方法はありません。さらに、フーリエ変換には断続的な正弦波の開始と終了をマークするメカニズムはありません。

この欠陥を修正しようとする中で、Dennis Gabor (1946) は、信号の "ウィンドウ処理" と呼ばれる、一度に解析するのは小さいセクションの信号のみにするという手法で、フーリエ変換を適合させました。ガボールの適合は短時間フーリエ変換 (STFT) と呼ばれます。この手法は、基本的に有限区間の場合のみ非ゼロである、時間関数またはウィンドウの選択によって機能します。1 つの例として、次のガウス ウィンドウ関数について考えます。

$$w(t)=\sqrt{\frac{\alpha }{\pi }}{e}^{-\alpha t^2}$$

ガウス関数の中心は、α の値に依存する区間上の t=0 のあたりになります。ガウス関数を τ だけシフトすると、次のような結果になります。

$$w(t-\tau )=\sqrt{\frac{\alpha }{\pi }}{e}^{-\alpha {(t-\tau )}^2},$$

中心は、τ のあたりのガウス ウィンドウです。信号を $$w(t-\tau )$$ で乗算すると、τ のあたりが中心となる信号の一部が選択されます。τ の異なる値に対して、これらのウィンドウ処理されたセグメントのフーリエ変換を行うと、STFT が生成されます。数学的には次のようになります。

$$F(\omega ,\tau )={\displaystyle \int f}(t)w(t-\tau )e^{-j\omega t}dt$$

STFT は、1 つの変数の関数を 2 つの変数 ω および τ の関数にマッピングします。この 1 次元信号の 2 次元表現は、STFT に冗長性があることを意味します。次の図は、STFT が信号を時間-周波数表現にマッピングする方法を示しています。

STFT は、信号の時間および周波数ベースの表示間のある種の妥協点を表します。これは、いつ、どの周波数で信号イベントが発生するかの両方に関する情報を提供します。ただし、この情報の取得ではその精度に制限があり、その精度はウィンドウのサイズによって決まります。

時間および周波数の情報間の STFT の妥協点は便利な一方で、時間枠の特定のサイズを選択すると、そのウィンドウがすべての周波数で同じになることが欠点です。多くの信号には、時間または周波数のいずれかをより正確に判別するためにウィンドウ サイズを可変にできるような、さらに柔軟なアプローチが必要です。

3 次元で STFT をプロットするのではなく、原則は、$$|F(\omega ,\tau )|$$ をカラー マップ上で強度としてコーディングすることです。以前に示した 2 つの異なる持続時間の 20 Hz の正弦波の STFT を計算して表示します。

STFT を使用することで、断続的な正弦波が 250 msec のあたりで開始して、750 msec のあたりで終了することがわかります。さらに、信号のエネルギーが 20 Hz のあたりに集中することがわかります。