このページの内容は最新ではありません。最新版の英語を参照するには、ここをクリックします。
bootstrp
ブートストラップ サンプリング
構文
説明
bootstat = bootstrp(___,Name,Value)
例
ブートストラッピングされた統計量の密度の推定
ブートストラッピングされた平均値のカーネル密度を推定します。
平均 5 をもつ指数分布から 100 個の乱数を生成します。
rng('default') % For reproducibility y = exprnd(5,100,1);
ベクトル y から取得した無作為な標本を使用して、100 個のブートストラッピングされた平均値の標本を計算します。
m = bootstrp(100,@mean,y);
ブートストラッピングされた平均値の密度の推定値をプロットします。
[fi,xi] = ksdensity(m); plot(xi,fi)
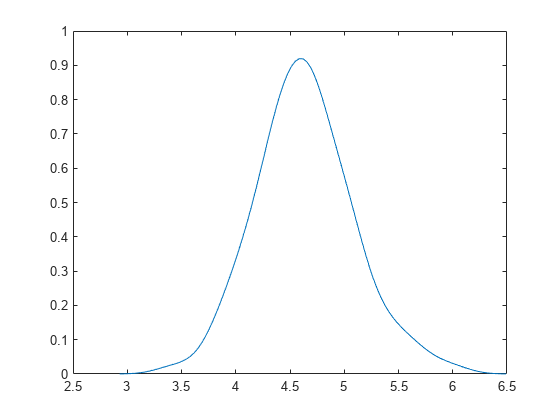
複数の統計値のブートストラッピング
100 個のブートストラップ標本の平均値と標準偏差を計算してプロットします。
平均 5 をもつ指数分布から 100 個の乱数を生成します。
rng('default') % For reproducibility y = exprnd(5,100,1);
ベクトル y から無作為に取得された標本により、100 個のブートストラッピングされた平均値と標準偏差の標本を計算します。
stats = bootstrp(100,@(x)[mean(x) std(x)],y);
ブートストラッピングされた推定値のペアをプロットします。
plot(stats(:,1),stats(:,2),'o') xlabel('Mean') ylabel('Standard Deviation')
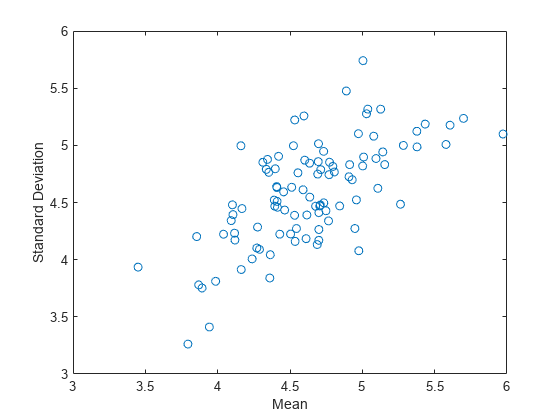
観測値のブートストラップ標本
患者データのブートストラップ標本を取得し、各データ標本の平均測定値を計算し、その結果を可視化します。
patients データセットを読み込みます。年齢、体重、身長の測定値が格納された行列 patientData を作成します。patientData の各行は、1 人の患者に対応します。
load patients
patientData = [Age Weight Height];patientData のデータから、200 個のブートストラップ データ標本を作成します。各標本を作成するため、patientData の行から、100 行 (すなわち size(patientData,1)) が復元抽出で無作為に選択されます。各標本について、年齢、体重、身長の測定値の平均を計算します。bootstat の各行には、1 つのブートストラップ標本に対する 3 つの平均測定値が格納されます。
rng('default') % For reproducibility bootstat = bootstrp(200,@mean,patientData);
200 個のすべてのブートストラップ データ標本について、平均測定値を可視化します。平均体重が大きいブートストラップ標本ほど平均身長が大きくなる傾向があることに注意してください。
scatter3(bootstat(:,1),bootstat(:,2),bootstat(:,3)) xlabel('Mean Age') ylabel('Mean Weight') zlabel('Mean Height') view([-75 10])
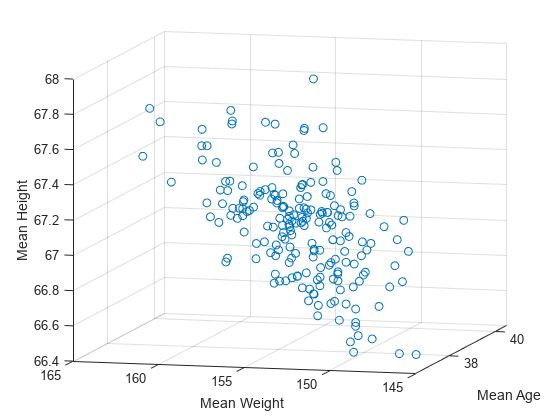
相関係数の標準誤差のブートストラッピング
標本データのブートストラップ リサンプリングを使用して、相関係数の標準誤差を計算します。
15 人の学生の LSAT スコアと法律学校の GPA の lawdata データセットを読み込みます。
load lawdata rng('default') % For reproducibility size(lsat)
ans = 1×2
15 1
size(gpa)
ans = 1×2
15 1
15 個のデータ点をリサンプリングして 1000 個のデータ標本を作成し、データ標本ごとに 2 つの変数の相関関係を計算します。
[bootstat,bootsam] = bootstrp(1000,@corr,lsat,gpa);
最初から 5 番目までのブートストラップ相関係数を表示します。
bootstat(1:5,:)
ans = 5×1
0.9874
0.4918
0.5459
0.8458
0.8959
最初から 5 番目までのブートストラップ標本について選択されたデータのインデックスを表示します。
bootsam(:,1:5)
ans = 15×5
13 3 11 8 12
14 7 1 7 4
2 14 5 10 8
14 12 1 11 11
10 15 2 12 14
2 10 13 5 15
5 1 11 11 9
9 13 5 10 3
15 15 15 3 3
15 11 1 2 4
⋮
すべてのブートストラップ標本間の相関係数のばらつきを示すヒストグラムを作成します。
histogram(bootstat)
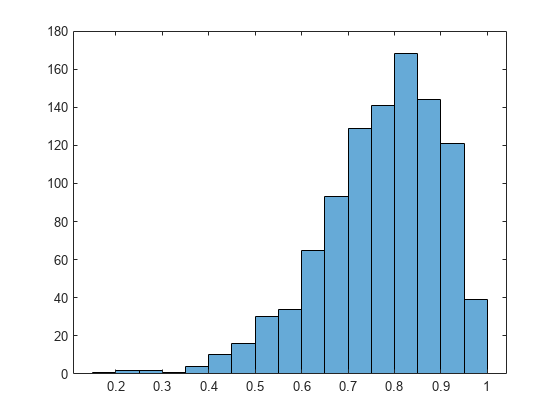
最小の標本は正の指標になっており、LSAT のスコアと GPA の関係が偶然でないことを示しています。
最後の推定相関係数の誤差のブートストラップ基準を計算します。
se = std(bootstat)
se = 0.1285
異なる観測値の重みをもつブートストラップ標本の比較
異なる観測値の重みをもつブートストラップ標本を比較します。各標本の統計量を計算するカスタム関数を作成します。
1 ~ 6 の数字から 50 個のブートストラップ標本を作成します。各標本を作成するため、bootstrp によって、1 ~ 6 の数字が復元抽出で無作為に 6 回選択されます。この処理は、サイコロを 6 回転がすのに似ています。カスタム関数 countfun (この例の終わりに掲載) を使用して、各標本内の 1 の数を数えます。
rng('default') %For reproducibility counts = bootstrp(50,@countfun,(1:6)');
メモ: この例のライブ スクリプト ファイルを使用している場合、関数 countfun は既にファイルの終わりに含まれています。それ以外の場合は、この関数を .m ファイルの終わりに作成するか、MATLAB® パス上のファイルとして追加する必要があります。
1 ~ 6 の数字から 50 個のブートストラップ標本を作成します。ただし、各値に異なる重みを割り当てます。bootstrp で 1 ~ 6 の数字を無作為に選択するとき、1 が選択される確率は常に 0.5、2 が選択される確率は常に 0.1 (以下同様) となります。再び、countfun を使用して各標本内の 1 の数をカウントします。
weights = [0.5 0.1 0.1 0.1 0.1 0.1]';
weightedCounts = bootstrp(50,@countfun,(1:6)','Weights',weights);ヒストグラムを使用して、2 つのブートストラップ標本のセットを比較します。
histogram(counts) hold on histogram(weightedCounts) legend xlabel('Number of 1s in Sample') ylabel('Number of Samples') hold off
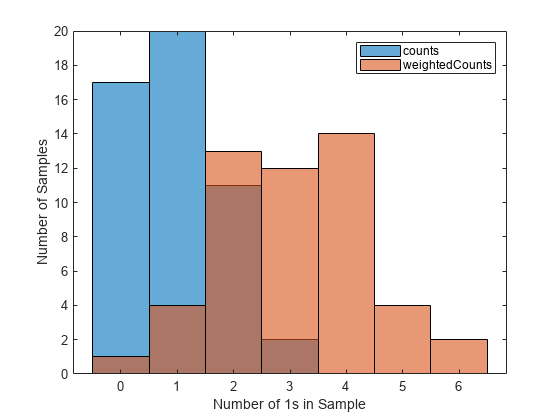
この 2 つのブートストラップ標本のセットは、分布が異なります。特に、2 番目のセットには 1 がより多く含まれる傾向があります。たとえば、最初のセットでは、50 個の標本のうち 1 の個数が 2 つよりも多い標本は 2 つしかありません。一方、2 番目のセット (観測値に重みが割り当てられたセット) では、50 個の標本のうち 1 の個数が 2 つよりも多い標本は 個あります。
次のコードは、関数 countfun を作成します。
function numberofones = countfun(sample) numberofones = sum(sample == 1); end
回帰モデルのブートストラッピング
残差をブートストラッピングして、線形回帰の係数ベクトルの標準誤差を推定します。
メモ: この例では regress を使用します。これは、回帰モデルの係数推定値または残差が必要な場合や、ブートストラッピングのようにモデルを複数回繰り返して当てはめる必要がある場合に便利です。当てはめた回帰モデルをさらに調べる必要がある場合は、fitlm を使用して線形回帰モデル オブジェクトを作成します。
標本データを読み込みます。
load hald線形回帰を実行し、残差を計算します。
x = [ones(size(heat)),ingredients]; y = heat; b = regress(y,x); yfit = x*b; resid = y - yfit;
残差をブートストラッピングして標準誤差を推定します。
se = std(bootstrp(1000,@(bootr)regress(yfit+bootr,x),resid))
se = 1×5
56.1752 0.5940 0.5815 0.5989 0.5691
入力引数
nboot — ブートストラップ標本の数
正の整数スカラー
ブートストラップ標本の数。正の整数スカラーとして指定します。各ブートストラップ標本を作成するため、bootstrp によって、d または d1,...,dN 内の n 行の (非スカラー) データから n 行が復元抽出で無作為に選択されます。
例: 100
データ型: single | double
bootfun — 各標本に適用する関数
関数ハンドル
各標本に適用する関数。関数ハンドルとして指定します。カスタム関数または組み込み関数を指定できます。bootfun は記号 @ を使用して指定しなければなりません。
カスタム関数を使用する例については、異なる観測値の重みをもつブートストラップ標本の比較を参照してください。
例: @mean
データ型: function_handle
d — 標本を取得する元のデータ
列ベクトル | 行列
標本を取得する元のデータ。列ベクトルまたは行列として指定します。d の n 行が観測値に対応します。複数のデータ入力引数 d1,...,dN を使用する場合、いくつかの引数をスカラー値として指定することができますが、非スカラー引数の行数はすべて同じでなければなりません。
単一のベクトル引数 d を使用する場合、それを行ベクトルとして指定できます。bootstrp は次に、ベクトルの要素からサンプルを抽出します。
データ型: single | double | logical | char | string | cell | categorical
名前と値の引数
オプションの引数のペアを Name1=Value1,...,NameN=ValueN として指定します。ここで Name は引数名、Value は対応する値です。名前と値の引数は他の引数の後ろにする必要がありますが、ペアの順序は関係ありません。
R2021a より前では、名前と値をそれぞれコンマを使って区切り、Name を引用符で囲みます。
例: bootstrp(4,@mean,(1:2)','Weights',[0.4 0.6]') は、1 ~ 2 の値から 4 つのブートストラップ標本を抽出し、各標本の平均を取ることを指定します。標本を抽出するときの、1 を得る確率は 0.4、2 を得る確率は 0.6 です。
Weights — 観測値の重み
ones(n,1)/n (既定値) | 非負のベクトル
観測値の重み。'Weights'、および正の要素を 1 つ以上含む非負のベクトルで構成される、コンマ区切りのペアとして指定します。Weights の要素数は、d または d1,...,dN のデータの行数 n と等しくなければなりません。1 つのブートストラップ標本を取得するために、bootstrp は、多項分布抽出確率として重みを使用し、n 行のデータから n 行を復元抽出で無作為に選択します。
データ型: single | double
Options — 並列計算と乱数設定のオプション
構造体
ブートストラップ反復の並列計算、およびブートストラップ サンプリング時の乱数設定のオプション。'Options' と構造体で構成されるコンマ区切りのペアとして指定します。statset を使用して Options 構造体を作成します。次の表は、オプションのフィールドとその値の一覧です。
| フィールド名 | 値 | 既定の設定 |
|---|---|---|
UseParallel | ブートストラップ反復を並列計算する場合は、この値を true に設定します。 | false |
UseSubstreams | 再生可能な方法で並列計算する場合は、この値を 再現性のある計算を行うには、 | false |
Streams | RandStream オブジェクトまたはそのようなオブジェクトの cell 配列としてこの値を指定します。UseParallel の値が true でなく、UseSubstreams の値も false でない場合、単一オブジェクトを使用します。この場合は、並列プールと同じサイズの cell 配列を使用します。 | Streams を指定しなかった場合、bootstrp は既定のストリームを使用します。 |
メモ
並列計算を行うには、Parallel Computing Toolbox™ が必要です。
例: 'Options',statset('UseParallel',true)
データ型: struct
出力引数
bootsam — ブートストラップ標本のインデックス
数値行列
ブートストラップ標本のインデックス。n 行 nboot 列の数値行列として返されます。ここで、n は元の非スカラー データの行数です。bootsam の各列は、1 つのブートストラップ標本に対応しており、標本を作成するために非スカラー データから抽出された行インデックスの値が格納されます。
たとえば、d1,...,dN の各データ入力引数が 16 個の値を含み、nboot = 4 の場合、bootsam は 16 行 4 列の行列となります。1 列目には最初のブートストラップ標本の d1,...,dN から抽出された 16 個の値のインデックスが格納され、2 列目には、2 番目のブートストラップ標本のインデックスが格納されます (以下同様)。ブートストラップ標本のインデックスは、すべての入力データセット d1,...,dN に対して同じです。
拡張機能
自動並列サポート
Parallel Computing Toolbox™ を使用して自動的に並列計算を実行することで、コードを高速化します。
並列実行するには、この関数を呼び出すときに名前と値の引数 Options を指定し、statset を使用してオプション構造体の UseParallel フィールドを true に設定します。
"Options",statset("UseParallel",true)
並列計算の詳細については、自動並列サポートを使用した MATLAB 関数の実行 (Parallel Computing Toolbox)を参照してください。
バージョン履歴
R2006a より前に導入
参考
histogram | bootci | ksdensity | parfor | random | randsample | RandStream | statget | statset
トピック
MATLAB コマンド
次の MATLAB コマンドに対応するリンクがクリックされました。
コマンドを MATLAB コマンド ウィンドウに入力して実行してください。Web ブラウザーは MATLAB コマンドをサポートしていません。

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)