このページの内容は最新ではありません。最新版の英語を参照するには、ここをクリックします。
grpdelay
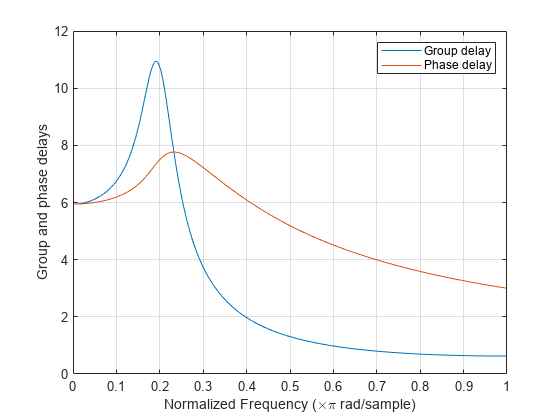
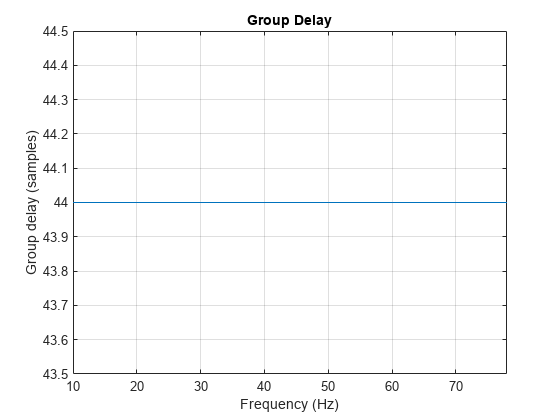
平均フィルター遅延 (群遅延)
構文
説明
出力引数なしで grpdelay(___) を使用すると、フィルターの群遅延応答がプロットされます。
例
入力引数
出力引数
詳細
拡張機能
バージョン履歴
R2006a より前に導入参考
cceps | designfilt | digitalFilter | fft | freqz | FVTool | hilbert | icceps | phasedelay | rceps