trapz
台形則による数値積分
説明
例
入力引数
詳細
ヒント
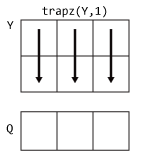
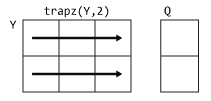
trapzとcumtrapzを使用して、離散データ セットで数値積分を実行します。データに関数式を使用できる場合は、代わりにintegral、integral2、またはintegral3を使用します。trapzは、演算対象の次元のサイズを 1 に減らし、最後の積分値のみを返します。cumtrapzは途中の積分値も返し、演算対象の次元のサイズを維持します。
拡張機能
バージョン履歴
R2006a より前に導入