svds
特異値とベクトルのサブセット
構文
説明
s = svds(A,k,sigma,Name,Value)svds(A,k,sigma,'Tolerance',1e-3) はアルゴリズムの収束の許容誤差を調整します。
例
最も大きい特異値
行列 A = delsq(numgrid('C',15)) は、区間 (0 8) において妥当に配置された特異値をもつ対称正定値行列です。最も大きい 6 個の特異値を計算します。
A = delsq(numgrid('C',15));
s = svds(A)s = 6×1
7.8666
7.7324
7.6531
7.5213
7.4480
7.3517
2 番目の入力に、計算する最も大きい特異値の数を指定します。
s = svds(A,3)
s = 3×1
7.8666
7.7324
7.6531
最も小さい特異値
行列 A = delsq(numgrid('C',15)) は、区間 (0 8) において妥当に配置された特異値をもつ対称正定値行列です。最も小さい 5 個の特異値を計算します。
A = delsq(numgrid('C',15)); s = svds(A,5,'smallest')
s = 5×1
0.5520
0.4787
0.3469
0.2676
0.1334
最も小さい非ゼロの特異値
スパースの 100 行 100 列のノイマン行列を作成します。
C = gallery('neumann',100);最も小さい 10 個の特異値を計算します。
ss = svds(C,10,'smallest')ss = 10×1
0.9828
0.9049
0.5625
0.5625
0.4541
0.4506
0.2256
0.1139
0.1139
0
最も小さい 10 個の非ゼロの特異値を計算します。行列にはゼロに等しい特異値があるため、'smallestnz' オプションによりその値が省略されます。
snz = svds(C,10,'smallestnz')snz = 10×1
0.9828
0.9828
0.9049
0.5625
0.5625
0.4541
0.4506
0.2256
0.1139
0.1139
関数ハンドルの使用による最も大きい特異値
スパース行列の右上および左下の非ゼロのブロックを表す 2 つの行列を作成します。
n = 500; B = rand(500); C = rand(500);
svds で使用できるように、Afun を現在のディレクトリに保存します。
function y = Afun(x,tflag,B,C,n) if strcmp(tflag,'notransp') y = [B*x(n+1:end); C*x(1:n)]; else y = [C'*x(n+1:end); B'*x(1:n)]; end
関数 Afun は B および C を使用して、実際にスパース行列 A = [zeros(n) B; C zeros(n)] 全体を作成することなく、指定されたフラグに応じて A*x または A'*x を計算します。これは行列のスパース パターンを利用して、A*x および A'*x を計算するときにメモリを節約します。
Afun を使用して、A の最も大きい 10 個の特異値を計算します。B、C および n を追加の入力として Afun に渡します。
s = svds(@(x,tflag) Afun(x,tflag,B,C,n),[1000 1000],10)
s = 250.3248 249.9914 12.7627 12.7232 12.6988 12.6608 12.6166 12.5643 12.5419 12.4512
A の最も大きい 10 個の特異値を直接計算して、結果と比較します。
A = [zeros(n) B; C zeros(n)]; s = svds(A,10)
s = 250.3248 249.9914 12.7627 12.7232 12.6988 12.6608 12.6166 12.5643 12.5419 12.4512
スパース行列の特異値分解
west0479 は、479 行 479 列の実数値のスパース行列です。この行列には、いくつかの大きい特異値と、多数の小さい特異値があります。
west0479 を読み込んで、A として格納します。
load west0479
A = west0479;A の特異値分解を計算し、最も大きい 6 個の特異値および対応する特異ベクトルを返します。特異値の収束を確認するために、4 番目の出力引数を指定します。
[U,S,V,cflag] = svds(A); cflag
cflag = 0
cflag は、すべての特異値が収束したことを示します。特異値は、出力行列 S の対角成分です。
s = diag(S)
s = 6×1
105 ×
3.1895
3.1725
3.1695
3.1685
3.1669
0.3038
A の完全な特異値分解を計算して、結果を確認します。A を非スパース行列に変換して、svd を使用します。
[U1,S1,V1] = svd(full(A));
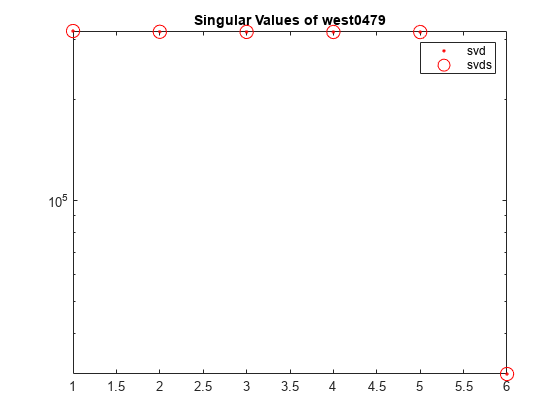
対数スケールを使用して svd と svds によって計算された A の最も大きい 6 個の特異値をプロットします。
s2 = diag(S1); semilogy(s2(1:6),'r.') hold on semilogy(s,'ro','MarkerSize',10) title('Singular Values of west0479') legend('svd','svds')
収束の問題を修正
スパース対角行列を作成して、最も大きい 6 個の特異値を計算します。
A = diag(sparse([1e4*ones(1, 8) 1e4:-1:1])); s = svds(A)
Warning: Only 2 of the 6 requested singular values converged. Singular values that did not converge are NaN.
s = 6×1
104 ×
1.0000
0.9999
NaN
NaN
NaN
NaN
svds によって警告が出力されます。これは最大回数の反復を実行したが、許容誤差に収まらなかったためです。
収束の問題を解決する最も効果的な方法は、'SubspaceDimension' により大きい値を使用することにより、計算に使用する Krylov 部分空間の最大サイズを増加することです。これを実行するには、60 の値を使用して 'SubspaceDimension' の名前と値のペアを渡します。
s = svds(A,6,'largest','SubspaceDimension',60)
s = 6×1
104 ×
1.0000
1.0000
1.0000
1.0000
1.0000
1.0000
QR 分解を使用して近特異行列の SVD を計算
近特異行列の最も小さい 10 個の特異値を計算します。
rng default format shortg B = spdiags([repelem([1; 1e-7], [198, 2]) ones(200, 1)], [0 1], 200, 200); s1 = svds(B,10,'smallest')
Warning: Large residual norm detected. This is likely due to bad condition of the input matrix (condition number 1.0008e+16).
s1 = 10×1
7.0945
7.0945
7.0945
7.0945
7.0945
7.0945
7.0945
7.0945
0.25927
7.0888e-16
警告は、svds が適切な特異値の計算に失敗したことを示します。svds が失敗した原因は、最小と最小から 2 番目の特異値の間にギャップがあるためです。svds(...,'smallest') は B の逆行列を計算する必要があり、これにより大きい数値誤差が発生しています。
比較のために、svd を使用して、正確な特異値を計算します。
s = svd(full(B)); s = s(end-9:end)
s = 10×1
0.14196
0.12621
0.11045
0.094686
0.078914
0.063137
0.047356
0.031572
0.015787
7.0888e-16
svds でこの計算を再現するために、B の QR 分解を行います。三角行列 R の特異値は、B と同じになります。
[Q,R,p] = qr(B,0);
R の各行のノルムをプロットします。
rownormR = sqrt(diag(R*R')); semilogy(rownormR) hold on; semilogy(size(R, 1), rownormR(end), 'ro')
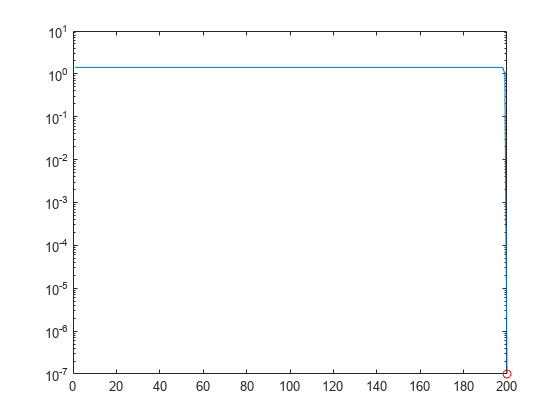
R の最後の要素はほぼゼロであるため、解が不安定になります。
この要素による悪い影響が解の正しい部分に及ばないように、R の最後の行を厳密にゼロに設定します。
R(end,:) = 0;
svds を使用して R の最も小さい 10 個の特異値を見つけます。結果は svd で得られたものと同等です。
sr = svds(R,10,'smallest')sr = 10×1
0.14196
0.12621
0.11045
0.094686
0.078914
0.063137
0.047356
0.031572
0.015787
0
この方法を使用して B の特異ベクトルを計算するには、 Q および置換ベクトル pを使用して左右の特異ベクトルを変換します。
[U,S,V] = svds(R,20,'s');
U = Q*U;
V(p,:) = V;入力引数
A — 入力行列
行列
入力行列。A は多くの場合、大規模なスパース行列です。
データ型: double
複素数のサポート: あり
k — 計算する特異値の数
スカラー
計算する特異値の数。正のスカラー整数として指定します。次のいずれかの条件が満たされる場合、svds は要求された数よりも少ない特異値を返します。
kがmin(size(A))より大きいsigma = 'smallestnz'、かつkがAの非ゼロの特異値の数より大きい
k が大きすぎる場合、svds はその値を有効な k の最大値に置き換えます。
例: svds(A,2) は、A の最も大きい 2 つの特異値を返します。
sigma — 特異値のタイプ
'largest' (既定値) | 'smallest' | 'smallestnz' | スカラー
特異値のタイプ。次の値のいずれかとして指定します。
| オプション | 説明 |
|---|---|
|
| 最も大きい特異値 |
| 最も小さい特異値 |
| 最も小さい非ゼロの特異値 |
スカラー | スカラーに最も近い特異値 |
例: svds(A,k,'smallest') は、最も小さい k 個の特異値を出力します。
例: svds(A,k,100) は、100 に最も近い k 個の特異値を計算します。
データ型: double | char | string
opts — オプション構造体
構造体
オプション構造体。次の表の 1 つ以上のフィールドを含む構造体として指定します。
メモ
オプション構造体を使用したオプションの指定は推奨されません。代わりに名前と値のペアを使用してください。
| オプション フィールド | 説明 | 名前と値のペア |
|---|---|---|
tol | 収束の許容誤差 | 'Tolerance' |
maxit | 最大反復回数 | 'MaxIterations' |
p | Krylov 部分空間の最大サイズ | 'SubspaceDimension' |
u0 | 左初期開始ベクトル | 'LeftStartVector' |
v0 | 右初期開始ベクトル | 'RightStartVector' |
disp | 診断情報の表示レベル | 'Display' |
fail | 出力内の収束しない特異値の処理 | 'FailureTreatment' |
メモ
数値スカラー シフト sigma を使用する場合、svds はオプション p を無視します。
例: opts.tol = 1e-6, opts.maxit = 500 は、フィールド tol および maxit に値が設定された構造体を作成します。
データ型: struct
Afun — 行列関数
関数ハンドル
行列関数。関数ハンドルとして指定します。関数 Afun は、次の条件を満たさなければなりません。
Afun(x,'notransp')はベクトルxを受け入れて、積A*xを返す。Afun(x,'transp')はベクトルxを受け入れて、積A'*xを返す。
メモ
関数ハンドルは、sigma = 'largest' (既定) の場合にのみ使用します。
例: svds(Afun,[1000 1200])
n — Afun で使用される行列のサイズ
2 要素ベクトル
Afun で使用される行列 A のサイズ。2 要素のサイズ ベクトル [m n] として指定します。
名前と値の引数
引数のオプションのペアを Name1=Value1,...,NameN=ValueN として指定します。ここで Name は引数名で、Value は対応する値です。名前と値の引数は他の引数の後になければなりませんが、ペアの順序は重要ではありません。
R2021a より前では、コンマを使用してそれぞれの名前と値を区切り、Name を引用符で囲みます。
例: s = svds(A,k,sigma,'Tolerance',1e-10,'MaxIterations',100) は収束の許容誤差を緩和し、より少ない反復回数を使用します。
Tolerance — 収束の許容誤差
1e-14 (既定値) | 非負の実数スカラー
収束の許容誤差。'Tolerance' と非負の実数値スカラーから構成されるコンマ区切りのペアとして指定します。
例: s = svds(A,k,sigma,'Tolerance',1e-3)
MaxIterations — アルゴリズムの最大反復回数
300 (既定値) | 正の整数
アルゴリズムの最大反復回数。'MaxIterations' と正の整数で構成されるコンマ区切りのペアとして指定します。
例: s = svds(A,k,sigma,'MaxIterations',350)
SubspaceDimension — Krylov 部分空間の最大サイズ
max(3*k,15) (既定値) | 非負の整数
Krylov 部分空間の最大サイズ。'SubspaceDimension' と非負の整数で構成されるコンマ区切りのペアとして指定します。'SubspaceDimension' の値は k + 2 以上でなければなりません。ここで、k は特異値の数です。
svds が収束しない問題では、'SubspaceDimension' の値を大きくすることで収束動作が改善される場合があります。
このオプションは、sigma の数値に対しては無視されます。
例: s = svds(A,k,sigma,'SubspaceDimension',25)
LeftStartVector — 左初期開始ベクトル
ベクトル
左初期開始ベクトル。'LeftStartVector' と数値ベクトルで構成されるコンマ区切りのペアとして指定します。
'LeftStartVector' または 'RightStartVector' のどちらか一方のみを指定できます。いずれのオプションも指定しない場合、m 行 n 列の行列 A の既定は次のとおりです。
m < n— 左初期開始ベクトルをrandn(m,1)に設定m >= n— 右初期開始ベクトルをrandn(n,1)に設定
異なる乱数開始ベクトルを指定する主な理由は、ベクトルの生成に使用する乱数ストリームを制御するためです。
メモ
svds は、プライベート乱数ストリームを使用する再現可能な方法で開始ベクトルを選択します。乱数のシードを変更しても、この randn の使用には "影響しません"。
例: s = svds(A,k,sigma,'LeftStartVector',randn(m,1)) は、グローバル乱数ストリームから値を取り出す乱数開始ベクトルを使用します。
データ型: double
RightStartVector — 右初期開始ベクトル
ベクトル
右初期開始ベクトル。'RightStartVector' と数値ベクトルで構成されるコンマ区切りのペアとして指定します。
'LeftStartVector' または 'RightStartVector' のどちらか一方のみを指定できます。いずれのオプションも指定しない場合、m 行 n 列の行列 A の既定は次のとおりです。
m < n— 左初期開始ベクトルをrandn(m,1)に設定m >= n— 右初期開始ベクトルをrandn(n,1)に設定
異なる乱数開始ベクトルを指定する主な理由は、ベクトルの生成に使用する乱数ストリームを制御するためです。
メモ
svds は、プライベート乱数ストリームを使用する再現可能な方法で開始ベクトルを選択します。乱数のシードを変更しても、この randn の使用には "影響しません"。
例: s = svds(A,k,sigma,'RightStartVector',randn(n,1)) は、グローバル乱数ストリームから値を取り出す乱数開始ベクトルを使用します。
データ型: double
FailureTreatment — 収束しない特異値の処理
'replacenan' | 'keep' | 'drop'
収束しない特異値の処理。'FailureTreatment' と、'replacenan'、'keep'、'drop' のいずれかのオプションから構成されるコンマ区切りのペアとして指定します。
'FailureTreatment' の値によって、収束しない特異値が出力でどのように表示されるが決定します。
| オプション | 出力への影響 |
|---|---|
|
| 収束しない特異値は出力から削除されます。その結果、 |
|
| 収束しない特異値は |
|
| 収束しない特異値は出力に含まれます。 |
例: s = svds(A,k,sigma,'FailureTreatment','drop') は収束しない特異値を出力から削除します。
データ型: char | string
Display — 診断情報の表示の切り替え
false (既定値) | true | 0 | 1
診断情報の表示の切り替え。false、true、0、または 1 として指定します。値が false または 0 の場合は表示がオフになり、値が true または 1 の場合は表示がオンになります。
出力引数
s — 特異値
列ベクトル
特異値。列ベクトルとして返されます。特異値は、非負の実数値であり、降順でリストされます。
U — 左特異ベクトル
行列
左特異ベクトル。行列の列として返されます。A が m 行 n 列の行列で、k 個の特異値を要求した場合、U は直交列をもつ m 行 k 列の行列になります。
マシン、MATLAB® のリリース、またはパラメーター (開始ベクトルや部分空間の次元など) が異なると、異なった特異ベクトルが生成されることがありますが、数値的にはいずれも正確です。U と V の対応する列で符号が反転する場合がありますが、これは、反転しても式 A = U*S*V' の値には影響がないためです。
S — 特異値
対角行列
特異値。対角行列として返されます。S の対角要素は非負の特異値です。A が m 行 n 列の行列で、k 個の特異値を要求した場合、S は k 行 k 列になります。
V — 右特異ベクトル
行列
右特異ベクトル。行列の列として返されます。A が m 行 n 列の行列で、k 個の特異値を要求した場合、V は直交列をもつ n 行 k 列の行列になります。
マシン、MATLAB のリリース、またはパラメーター (開始ベクトルや部分空間の次元など) が異なると、異なった特異ベクトルが生成されることがありますが、数値的にはいずれも正確です。U と V の対応する列で符号が反転する場合がありますが、これは、反転しても式 A = U*S*V' の値には影響がないためです。
flag — 収束フラグ
スカラー
収束フラグ。スカラーとして返されます。値 0 は、すべての特異値が収束したことを示します。それ以外の場合、一部の特異値が収束していません。
この収束フラグ出力を使用すると、失敗した収束に関する警告が非表示になります。
ヒント
svdsketchは、svdsにどのランクを指定するかは事前にわからないが、SVD の近似が満たすべき許容誤差はわかる場合に有用です。svdsは、複数の実行にわたって再現性を確保するために、プライベート乱数ストリームを使用して既定の開始ベクトルを生成します。svdsを呼び出す前にrngを使用して乱数発生器の状態を設定しても、出力に影響しません。svdsを使用する方法は、小規模で密度の高い行列の特異値をいくつか求めるときに最も効率的な方法とは言えません。このような問題では、svd(full(A))を使用する方が迅速な場合があります。たとえば、500 行 500 列の行列の特異値を 3 個求める問題は、比較的小規模の問題であるためsvdで容易に処理できます。指定された行列で
svdsが収束しない場合は、'SubspaceDimension'の値を増加することにより Krylov 部分空間のサイズを増加します。補助的な選択肢として、反復の最大回数 ('MaxIterations') と収束の許容誤差 ('Tolerance') を調整することも、収束動作に役立つ場合があります。kを増加することでパフォーマンスが向上することがあり、特に行列に繰り返される特異値がある場合に効果的です。
参照
[1] Baglama, J. and L. Reichel, “Augmented Implicitly Restarted Lanczos Bidiagonalization Methods.” SIAM Journal on Scientific Computing. Vol. 27, 2005, pp. 19–42.
[2] Larsen, R. M. “Lanczos Bidiagonalization with partial reorthogonalization.” Dept. of Computer Science, Aarhus University. DAIMI PB-357, 1998.
拡張機能
スレッドベースの環境
MATLAB® の backgroundPool を使用してバックグラウンドでコードを実行するか、Parallel Computing Toolbox™ の ThreadPool を使用してコードを高速化します。
この関数はスレッドベースの環境を完全にサポートしています。詳細については、スレッドベースの環境での MATLAB 関数の実行を参照してください。
GPU 配列
Parallel Computing Toolbox™ を使用してグラフィックス処理装置 (GPU) 上で実行することにより、コードを高速化します。
使用上の注意事項および制限事項:
sigmaパラメーターを指定する場合は、値を'largest'にしなければなりません。
詳細については、GPU での MATLAB 関数の実行 (Parallel Computing Toolbox)を参照してください。
分散配列
Parallel Computing Toolbox™ を使用して、クラスターの結合メモリ上で大きなアレイを分割します。
使用上の注意事項および制限事項:
sigmaパラメーターを指定する場合は、値を'largest'にしなければなりません。
詳細については、分散配列を使用した MATLAB 関数の実行 (Parallel Computing Toolbox)を参照してください。
バージョン履歴
R2006a より前に導入R2016a: 再現性についての変更点
再現性
svdsを複数回続けて呼び出しても、同じ結果が生成されるようになりました。この動作を変更するには、次を行います。R2017a 以前では、オプション構造体の
u0またはv0フィールドをランダム ベクトルに設定します。R2017b 以降では、
'LeftStartVector'または'RightStartVector'をランダム ベクトルに設定することが推奨されます。
MATLAB コマンド
次の MATLAB コマンドに対応するリンクがクリックされました。
コマンドを MATLAB コマンド ウィンドウに入力して実行してください。Web ブラウザーは MATLAB コマンドをサポートしていません。

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)