pchip
区分的 3 次エルミート内挿多項式 (PCHIP)
説明
例
spline、pchip および makima によるデータ内挿
2 つの異なるデータ セットについて、spline、pchip、makima で生成された内挿結果を比較します。これらの関数はすべて、異なる形式の区分的 3 次エルミート内挿を実行します。内挿の勾配の計算方法が各関数で異なるため、基となるデータに変動の少ない領域やうねりがある場合の動作も異なります。
変動の少ない領域を接続するサンプル データの内挿結果を比較します。x の値のベクトル、点 y での関数値、クエリ点 xq を作成します。spline、pchip、および makima を使用して、クエリ点での内挿を計算します。比較のため、クエリ点での内挿関数値をプロットします。
x = -3:3; y = [-1 -1 -1 0 1 1 1]; xq1 = -3:.01:3; p = pchip(x,y,xq1); s = spline(x,y,xq1); m = makima(x,y,xq1); plot(x,y,'o',xq1,p,'-',xq1,s,'-.',xq1,m,'--') legend('Sample Points','pchip','spline','makima','Location','SouthEast')

ここでは、pchip と makima が、オーバーシュートを起こさずに変動の少ない領域を正確に接続できるという点で同じような動作を示しています。
振動サンプル関数を使用して、2 回目の比較を行います。
x = 0:15; y = besselj(1,x); xq2 = 0:0.01:15; p = pchip(x,y,xq2); s = spline(x,y,xq2); m = makima(x,y,xq2); plot(x,y,'o',xq2,p,'-',xq2,s,'-.',xq2,m,'--') legend('Sample Points','pchip','spline','makima')
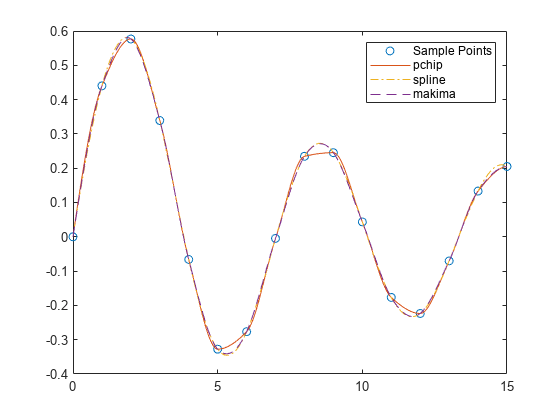
基となる関数が振動関数である場合、局所的極値付近での強引な変動が少ない pchip よりも、spline と makima の方が点の間の動きをより良好にキャプチャします。
区分的多項式構造体による内挿
x の値と関数値 y のベクトルを作成し、pchip を使用して区分的多項式構造体を作成します。
x = -5:5; y = [1 1 1 1 0 0 1 2 2 2 2]; p = pchip(x,y);
この構造体を ppval で使用し、複数のクエリ点で内挿を評価します。結果をプロットします。
xq = -5:0.2:5; pp = ppval(p,xq); plot(x,y,'o',xq,pp,'-.') ylim([-0.2 2.2])

入力引数
x — サンプル点
ベクトル
サンプル点。ベクトルとして指定します。ベクトル x は、データ y が与えられる時点を指定します。x の要素は一意でなければなりません。
データ型: single | double
y — サンプル点での関数値
ベクトル | 行列 | 配列
サンプル点での関数値。数値ベクトル、行列または配列として指定します。x と y は同じ長さでなければなりません。
y が行列または配列の場合、最後の次元の値 y(:,...,:,j) が x に一致させる値として使用されます。この場合、y の最後の次元は x と同じ長さでなければなりません。
データ型: single | double
xq — クエリ点
スカラー | ベクトル | 行列 | 配列
クエリ点。スカラー、ベクトル、行列または配列として指定します。xq で指定された点は、pchip により計算された内挿関数値 yq の x 座標です。
データ型: single | double
出力引数
p — クエリ点における内挿値
スカラー | ベクトル | 行列 | 配列
クエリ点における内挿値。スカラー、ベクトル、行列または配列として返されます。p のサイズは、y と xq のサイズに関連しています。
yがベクトルの場合、pのサイズはxqと同じです。yがサイズNy = size(y)の配列の場合、以下の条件が適用されます。xqがスカラーまたはベクトルの場合、size(p)は[Ny(1:end-1) length(xq)]を返す。xqが配列の場合、size(p)は[Ny(1:end-1) size(xq)を返す。
pp — 区分的多項式
構造体
区分的多項式。構造体として返されます。この構造体を関数 ppval とあわせて使用し、1 つ以上のクエリ点で内挿多項式を評価します。これらの構造体には次のフィールドがあります。
| フィールド | 説明 |
|---|---|
form | "区分的多項式" の場合 |
breaks | 長さ |
coefs |
|
pieces | 区分の数 ( |
order | 多項式の次数 |
dim | ターゲットの次元 |
coefs の多項式係数は各区間の局所的な係数であるため、従来の多項方程式で係数を使用するには対応する節点区間の下限端点を減算しなければなりません。言い換えれば、区間 [x1,x2] の係数 [a,b,c,d] について、対応する多項式は次のようになります。
詳細
形状維持区分的 3 次内挿
pchip は、次のプロパティを使用して区分的 3 次多項式 を内挿します。
各部分区間 での多項式 は、内挿点に指定された導関数 (勾配) をもつ特定のデータ点では、3 次エルミート内挿多項式です。
は y を内挿します。すなわち が成立します。1 次導関数 は連続しています。2 次導関数 は連続しない可能性が高いため、 でのジャンプが可能です。
3 次内挿 は形状維持内挿です。 での勾配は、 がデータの形状や単調性を保持するように選択されます。したがって、データが単調な区間では も単調になり、データが局所的な極値をもつ点では も局所的な極値をもちます。
メモ
y が行列の場合、 は y の各行についてこれらのプロパティを満たします。
ヒント
splineは、pchipが を構築する方法とほぼ同じ方法で を構築します。ただし、splineは で異なる勾配、つまり も連続になる勾配を選択します。この差異により、いくつかの影響が生じます。splineでは、 が連続になるような、より平滑な結果が生成されます。関数
splineは、データが平滑関数の値の場合、より正確になります。関数
pchipは、データが平滑でない場合、オーバーシュートが生じず、振動が少なくなります。関数
pchipは、セットアップが簡単です。2 つとも計算量が多くなります。
参照
[1] Fritsch, F. N. and R. E. Carlson. "Monotone Piecewise Cubic Interpolation." SIAM Journal on Numerical Analysis. Vol. 17, 1980, pp.238–246.
[2] Kahaner, David, Cleve Moler, Stephen Nash. Numerical Methods and Software. Upper Saddle River, NJ: Prentice Hall, 1988.
拡張機能
C/C++ コード生成
MATLAB® Coder™ を使用して C および C++ コードを生成します。
使用上の注意事項および制限事項:
入力
xは厳密に増加するものでなければなりません。コード生成では、値が
NaNのyエントリは削除されません。pp = pchip(x,y)構文のコードを生成する場合は、MATLAB® で関数ppvalにppを入力できません。コード ジェネレーターで作成されたpp構造体から MATLAB のpp構造体を作成するには、以下のように実行します。コード生成では、
unmkppを使用して区分的多項式の詳細を MATLAB に返します。MATLAB では、
mkppを使用してpp構造体を作成します。
スレッドベースの環境
MATLAB® の backgroundPool を使用してバックグラウンドでコードを実行するか、Parallel Computing Toolbox™ の ThreadPool を使用してコードを高速化します。
この関数はスレッドベースの環境を完全にサポートしています。詳細については、スレッドベースの環境での MATLAB 関数の実行を参照してください。
GPU 配列
Parallel Computing Toolbox™ を使用してグラフィックス処理装置 (GPU) 上で実行することにより、コードを高速化します。
この関数は GPU 配列を完全にサポートしています。詳細については、GPU での MATLAB 関数の実行 (Parallel Computing Toolbox)を参照してください。
分散配列
Parallel Computing Toolbox™ を使用して、クラスターの結合メモリ上で大きなアレイを分割します。
使用上の注意事項および制限事項:
構文
pchip(は分散配列ではサポートされていません。x,y)
詳細については、分散配列を使用した MATLAB 関数の実行 (Parallel Computing Toolbox)を参照してください。
バージョン履歴
R2006a より前に導入
MATLAB コマンド
次の MATLAB コマンドに対応するリンクがクリックされました。
コマンドを MATLAB コマンド ウィンドウに入力して実行してください。Web ブラウザーは MATLAB コマンドをサポートしていません。

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)