gammaincinv
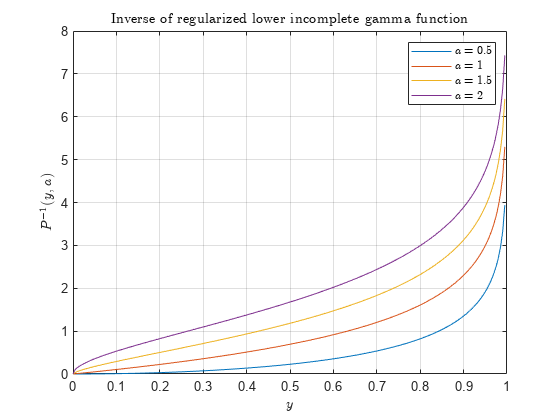
正則化された不完全ガンマ関数の逆関数
説明
例
入力引数
詳細
ヒント
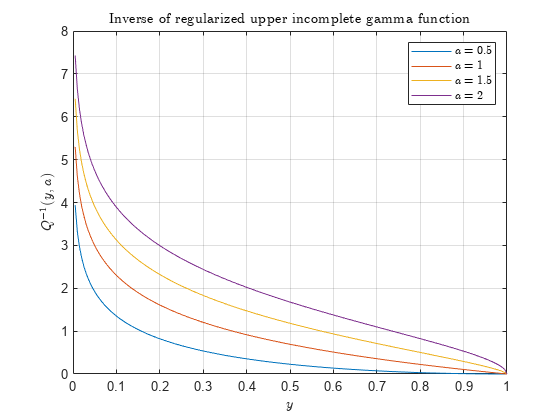
正則化された上側不完全ガンマ関数が 0 に近い場合、
'upper'オプションを指定して上側の逆関数を計算するほうが、1 から正則化された下側不完全ガンマ関数を減算してから下側の逆関数を求めるよりも正確です。
参照
[1] Olver, F. W. J., A. B. Olde Daalhuis, D. W. Lozier, B. I. Schneider, R. F. Boisvert, C. W. Clark, B. R. Miller, and B. V. Saunders, eds., Chapter 8. Incomplete Gamma and Related Functions, NIST Digital Library of Mathematical Functions, Release 1.0.22, Mar. 15, 2018.