このページの内容は最新ではありません。最新版の英語を参照するには、ここをクリックします。
dot
ドット積
説明
例
実数ベクトルのドット積
単純な 3 要素のベクトルを 2 つ作成します。
A = [4 -1 2]; B = [2 -2 -1];
A と B のドット積を計算します。
C = dot(A,B)
C = 8
次により、結果は 8 になります。
C = A(1)*B(1) + A(2)*B(2) + A(3)*B(3)
複素数ベクトルのドット積
2 つの複素数ベクトルを作成します。
A = [1+i 1-i -1+i -1-i]; B = [3-4i 6-2i 1+2i 4+3i];
A と B のドット積を計算します。
C = dot(A,B)
C = 1.0000 - 5.0000i
A と B が複素数であるため、結果は複素数スカラーになります。一般的には、2 つの複素数ベクトルのドット積は複素数になります。例外は、複素数ベクトルとそれ自身のドット積を取る場合です。
A とそれ自身の内積を求めます。
D = dot(A,A)
D = 8
結果は、実数スカラーになります。ベクトルとそれ自身の内積は、ベクトルのユークリッド長 norm(A) に関係します。
行列のドット積
2 つの行列を作成します。
A = [1 2 3;4 5 6;7 8 9]; B = [9 8 7;6 5 4;3 2 1];
A と B のドット積を求めます。
C = dot(A,B)
C = 1×3
54 57 54
結果の C には 3 つの別個のドット積が含まれます。dot は A と B の列をベクトルとして扱い、対応する列のドット積を計算します。そのため、たとえば、C(1) = 54 は A(:,1) と B(:,1) のドット積です。
"行" をベクトルとして扱い、A と B のドット積を求めます。
D = dot(A,B,2)
D = 3×1
46
73
46
この場合、D(1) = 46 が A(1,:) と B(1,:) のドット積です。
多次元配列のドット積
2 つの多次元配列を作成します。
A = cat(3,[1 1;1 1],[2 3;4 5],[6 7;8 9])
A =
A(:,:,1) =
1 1
1 1
A(:,:,2) =
2 3
4 5
A(:,:,3) =
6 7
8 9
B = cat(3,[2 2;2 2],[10 11;12 13],[14 15; 16 17])
B =
B(:,:,1) =
2 2
2 2
B(:,:,2) =
10 11
12 13
B(:,:,3) =
14 15
16 17
3 番目の次元 (dim = 3) に沿って A と B のドット積を計算します。
C = dot(A,B,3)
C = 2×2
106 140
178 220
結果の C には 4 つの別個のドット積が含まれます。最初のドット積 C(1,1) = 106 は A(1,1,:) と B(1,1,:) のドット積に等しくなります。
入力引数
A,B — 入力配列
数値配列
入力配列。数値配列として指定します。
データ型: single | double
複素数のサポート: あり
dim — 演算の対象の次元
正の整数スカラー
演算の対象の次元。正の整数のスカラーとして指定します。値が指定されていない場合、既定値はサイズが 1 ではない最初の配列次元です。
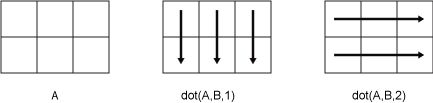
2 つの 2 次元の入力配列 A と B について考えます。
dot(A,B,1)はAとBの列をベクトルとして扱い、対応する列のドット積を返します。dot(A,B,2)はAとBの行をベクトルとして扱い、対応する行のドット積を返します。
dim が ndims(A) より大きい場合、dot は conj(A).*B を返します。
詳細
スカラーのドット積
長さ n の 2 つの実数ベクトルのスカラーのドット積は次のようになります。
実数ベクトルの場合、この関係は可換であり、dot(u,v) と dot(v,u) は等しくなります。ドット積が 0 の場合、u と v は垂直になります。
複素数ベクトルの場合、ドット積には複素共役が含まれます。これにより、任意のベクトルとそれ自身のドット積は必ず実数の正定値になります。
実数ベクトルの関係とは異なり、複素数の関係は可換ではなく、dot(u,v) は conj(dot(v,u)) と等しくなります。
アルゴリズム
入力
AおよびBが実数または複素数のベクトルの場合、関数dotはそれらを列ベクトルとして扱い、dot(A,B)はsum(conj(A).*B)と同じになります。入力が行列または多次元配列の場合、
dim引数により関数sumで演算を行う次元が決定されます。この場合、dot(A,B)はsum(conj(A).*B,dim)と同じになります。
拡張機能
tall 配列
メモリの許容量を超えるような多数の行を含む配列を計算します。
この関数は tall 配列を制限付きでサポートしています。
構文 dot(A,B) では、配列 A と配列 B は、それらがベクトルの場合でも同じサイズでなければなりません。
詳細については、メモリに収まらないデータの tall 配列を参照してください。
C/C++ コード生成
MATLAB® Coder™ を使用して C および C++ コードを生成します。
使用上の注意事項および制限事項:
コード生成では、この関数のスパース行列入力はサポートされません。
スレッドベースの環境
MATLAB® の backgroundPool を使用してバックグラウンドでコードを実行するか、Parallel Computing Toolbox™ の ThreadPool を使用してコードを高速化します。
この関数はスレッドベースの環境を完全にサポートしています。詳細については、スレッドベースの環境での MATLAB 関数の実行を参照してください。
GPU 配列
Parallel Computing Toolbox™ を使用してグラフィックス処理装置 (GPU) 上で実行することにより、コードを高速化します。
この関数は GPU 配列を完全にサポートしています。詳細については、GPU での MATLAB 関数の実行 (Parallel Computing Toolbox)を参照してください。
分散配列
Parallel Computing Toolbox™ を使用して、クラスターの結合メモリ上で大きなアレイを分割します。
この関数は分散配列を完全にサポートしています。詳細については、分散配列を使用した MATLAB 関数の実行 (Parallel Computing Toolbox)を参照してください。
バージョン履歴
R2006a より前に導入
参考
cross | sum | conj | norm | tensorprod
MATLAB コマンド
次の MATLAB コマンドに対応するリンクがクリックされました。
コマンドを MATLAB コマンド ウィンドウに入力して実行してください。Web ブラウザーは MATLAB コマンドをサポートしていません。

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)