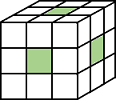
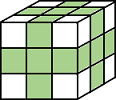
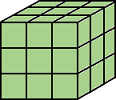
bwlabeln
バイナリ イメージ内の連結要素をラベル付け
説明
例
入力引数
出力引数
ヒント
この関数は、各要素の
top-left極値を基準に、連結要素を左から右に並べ替えます。複数の要素の水平位置が同じ場合、関数はそれらの要素を上から下に並べ替えた後、より高い次元に沿って再度並べ替えます。次の図は、2 つの異なる 2 次元領域の極値を示しています。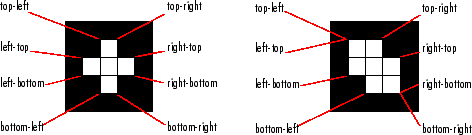
関数
bwlabel、bwlabeln、およびbwconncompはすべて、バイナリ イメージの連結要素を計算します。bwconncompは使用するメモリが大幅に少なく、場合によっては他の関数よりも高速です。関数 入力次元 出力形式 メモリの使用 連結性 bwlabel2 次元 倍精度をもつラベル行列 高 4 または 8 bwlabelnN 次元 倍精度ラベル行列 高 任意 bwconncompN 次元 CC構造体低 任意 既定の連結性を持つ
regionpropsを使用してバイナリ イメージから特徴を抽出するには、regionprops(BW)コマンドを使用してBWを直接regionpropsに渡します。
アルゴリズム
bwlabeln では、次の一般的な処理が使用されます。
すべてのイメージ ピクセルをスキャンし、非ゼロ ピクセルに予備ラベルを割り当て、ラベル等価を和集合検出テーブルに記録します。
和集合検出アルゴリズム [1] を使用して、等価クラスを解決します。
対応済みの等価クラスに基づいて、ピクセルの再ラベル付けを行います。
参照
[1] Sedgewick, Robert, Algorithms in C, 3rd Ed., Addison-Wesley, 1998, pp. 11-20.
拡張機能
バージョン履歴
R2006a より前に導入参考
bwconncomp | bwlabel | labelmatrix | label2rgb | regionprops