このページの内容は最新ではありません。最新版の英語を参照するには、ここをクリックします。
cordicrotate
CORDIC ベースの近似を使用して入力を回転
構文
v = cordicrotate(theta,u)
v = cordicrotate(theta,u,niters)
v = cordicrotate(theta,u,Name,Value)
v = cordicrotate(theta,u,niters,Name,Value)
説明
v = cordicrotate(theta,u)u が theta だけ回転されます。この関数では、u .* e^(j*theta) の結果が返されます。
v = cordicrotate(theta,u,niters)niters 回実行されます。
v = cordicrotate(theta,u,Name,Value)b に基づいて、出力がスケールされます。
v = cordicrotate(theta,u,niters,Name,Value)Name,Value の組の両方が指定されます。
入力引数
|
|
|
|
|
|
|
既定値: true |
出力引数
|
入力 入力 u が "符号なし" の整数または固定小数点の場合、出力 |
例
次のコードを実行して、CORDIC ベースの複雑な回転の精度を評価します。
wrdLn = 16;
theta = fi(-pi/3, 1, wrdLn);
u = fi(0.25 - 7.1i, 1, wrdLn);
uTeTh = double(u) .* exp(1i * double(theta));
fprintf('\n\nNITERS\tReal\t ERROR\t LSBs\t\tImag\tERROR\tLSBs\n');
fprintf('------\t-------\t ------\t ----\t\t-------\t------\t----\n');
for niters = 1:(wrdLn - 1)
v_fi = cordicrotate(theta, u, niters);
v_dbl = double(v_fi);
x_err = abs(real(v_dbl) - real(uTeTh));
y_err = abs(imag(v_dbl) - imag(uTeTh));
fprintf('%d\t%1.4f\t %1.4f\t %1.1f\t\t%1.4f\t %1.4f\t %1.1f\n',...
niters, real(v_dbl),x_err,(x_err * pow2(v_fi.FractionLength)), ...
imag(v_dbl),y_err, (y_err * pow2(v_fi.FractionLength)));
end
fprintf('\n');
以下のような出力テーブルが表示されます。
NITERS Real ERROR LSBs Imag ERROR LSBs ------ ------- ------ ---- ------- ------ ------ 1 -4.8438 1.1800 4833.5 -5.1973 1.4306 5859.8 2 -6.6567 0.6329 2592.5 -2.4824 1.2842 5260.2 3 -5.8560 0.1678 687.5 -4.0227 0.2560 1048.8 4 -6.3098 0.2860 1171.5 -3.2649 0.5018 2055.2 5 -6.0935 0.0697 285.5 -3.6528 0.1138 466.2 6 -5.9766 0.0472 193.5 -3.8413 0.0746 305.8 7 -6.0359 0.0121 49.5 -3.7476 0.0191 78.2 8 -6.0061 0.0177 72.5 -3.7947 0.0280 114.8 9 -6.0210 0.0028 11.5 -3.7710 0.0043 17.8 10 -6.0286 0.0048 19.5 -3.7590 0.0076 31.2 11 -6.0247 0.0009 3.5 -3.7651 0.0015 6.2 12 -6.0227 0.0011 4.5 -3.7683 0.0017 6.8 13 -6.0237 0.0001 0.5 -3.7666 0.0001 0.2 14 -6.0242 0.0004 1.5 -3.7656 0.0010 4.2 15 -6.0239 0.0001 0.5 -3.7661 0.0005 2.2
詳細
詳細
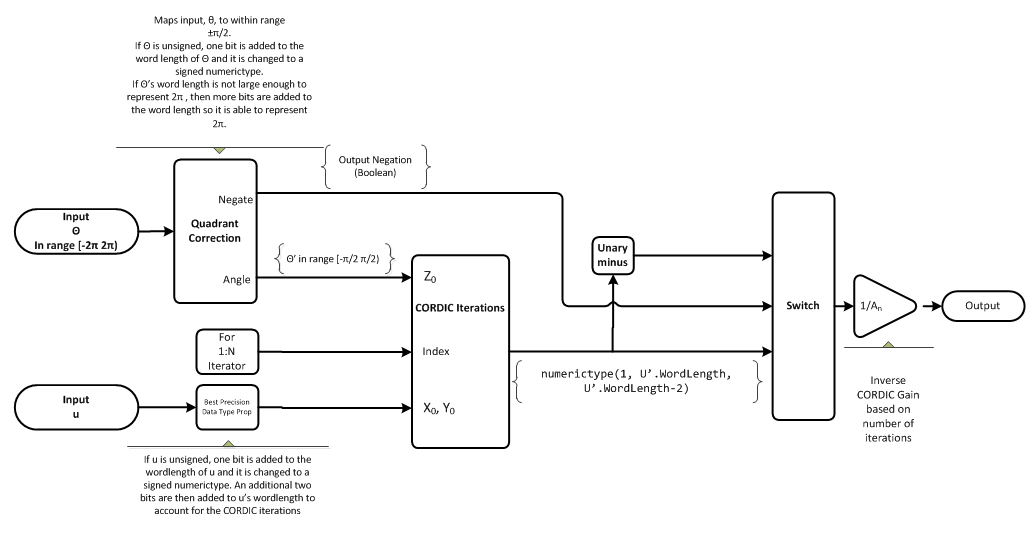
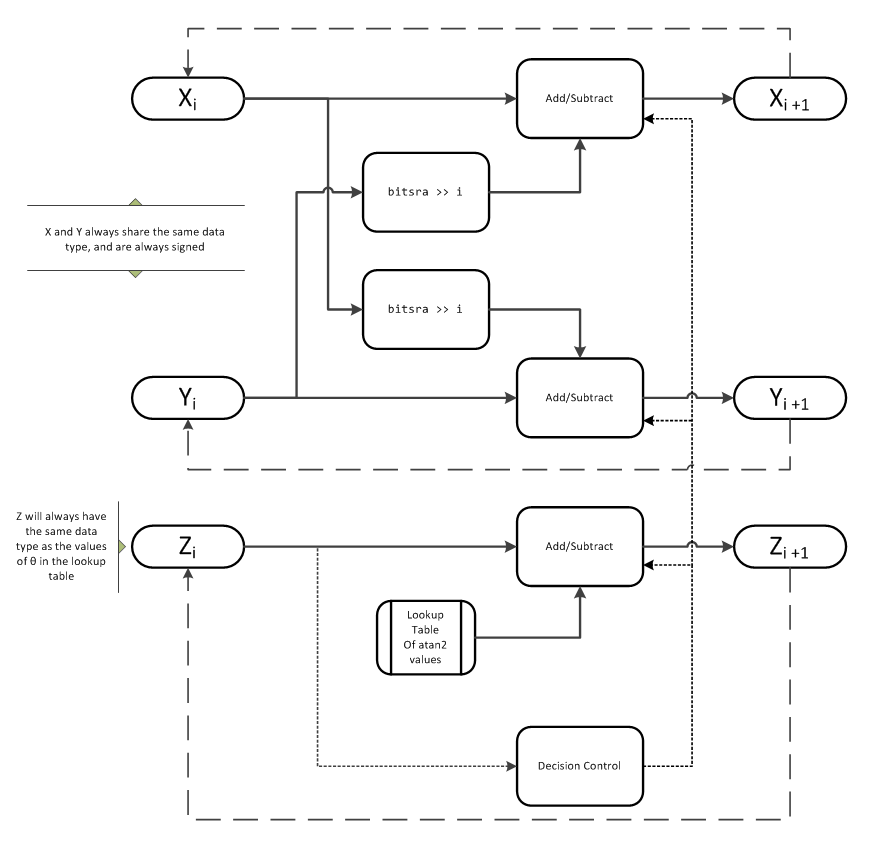
アルゴリズム
拡張機能
バージョン履歴
R2011a で導入