Symbolic Math Toolbox には、シンボリック数式の求解、プロット、および操作を行うための関数が用意されています。シンボリックな数学コードを作成、実行、および共有することができます。MATLAB ライブエディターでは、シンボリック ワークフローの次の手順の提案が示されます。このツールボックスには、微積分、線形代数、代数方程式および微分方程式、方程式の単純化、数式処理などの一般的な数学分野の関数が用意されています。
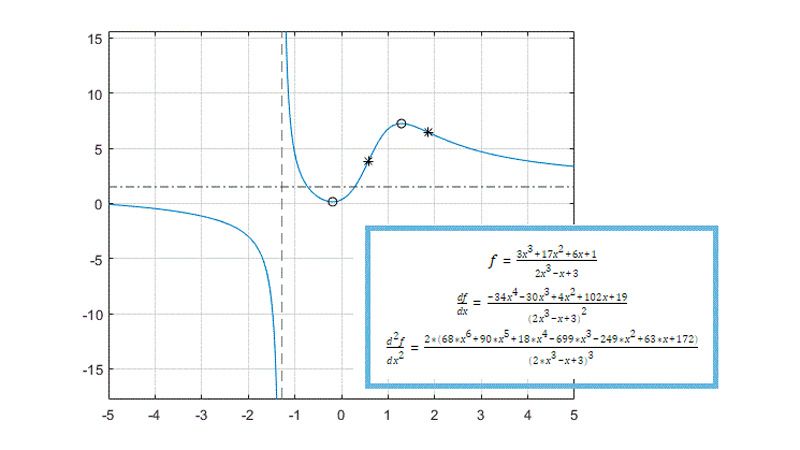
Symbolic Math Toolbox を使用することで、微分、積分、簡素化、変換、方程式の求解などを解析的に実行できます。また、次元計算や単位間の変換を実行することができます。計算は、解析的に、または可変精度の演算を使用して実行でき、結果が数学的表現で表示されます。
シンボリックな作業内容をライブスクリプトとして他の MATLAB ユーザーと共有したり、HTML、Word、LaTeX、PDF ドキュメントに変換したりすることができます。MATLAB 関数、Simulink Function ブロック、および Simscape 方程式をシンボリック式から直接生成できます。
可視化
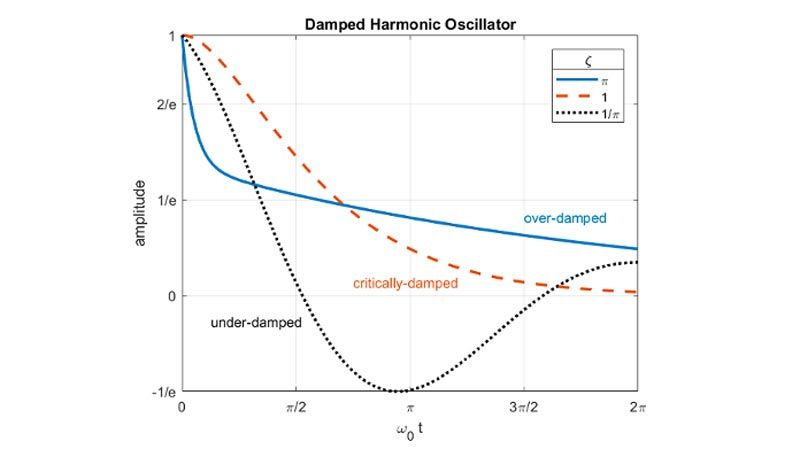
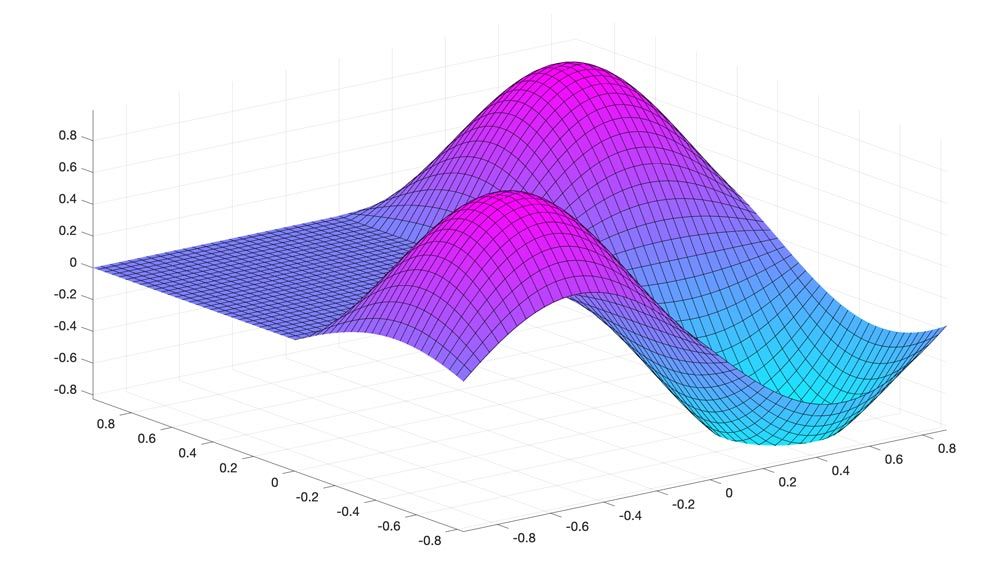
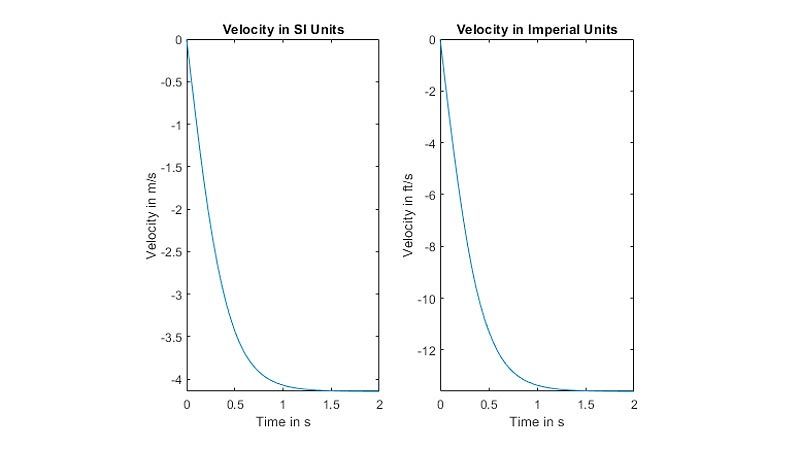
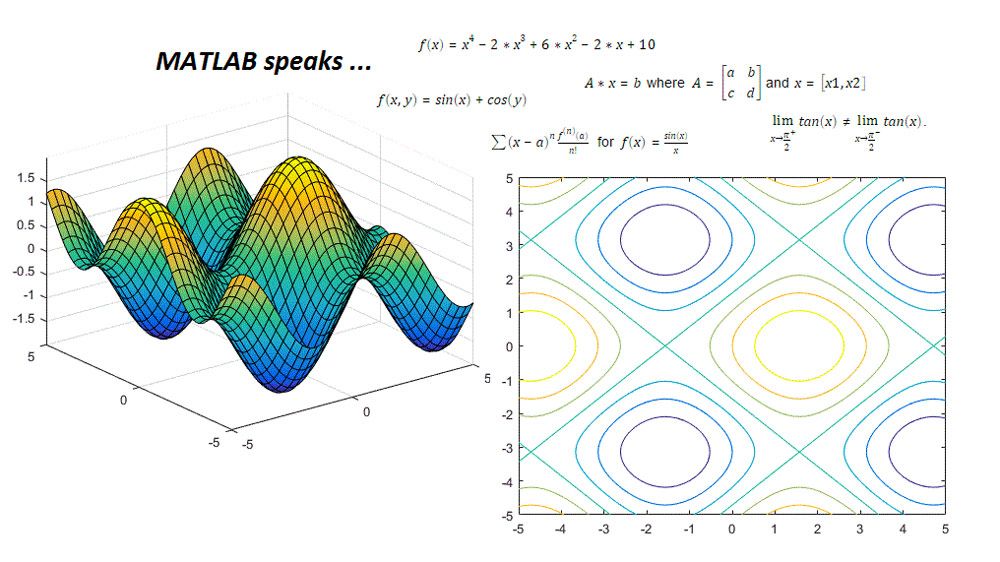
組み込み関数を用いて、拡張された MATLAB グラフィックス機能を使用してシンボリック式と関数をプロットし、アニメーションを使用してシンボリック式の動作を可視化します。
ドキュメンテーション | 例
ドキュメンテーションおよび共有
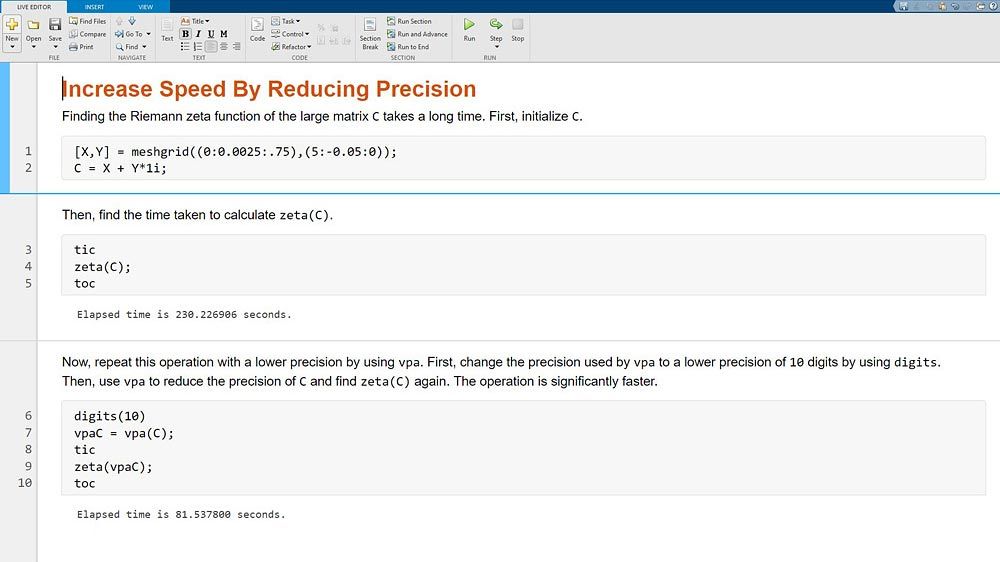
MATLAB ライブエディターを使用して、シンボリック数学計算を対話的に更新して表示すると、シンボリック ワークフローの次の手順が提案されます。作業をライブスクリプトとして共有するか、コードをパブリッシュして HTML、Word、LaTeX、PDF などに書式設定されたドキュメントを作成します。
ドキュメンテーション | 例
コード生成
MATLAB 関数、Simulink Function ブロック、カスタム方程式に基づいた Simscape コンポーネント、C コードや Fortran コードをシンボリック式から直接生成します。
ドキュメンテーション | 例
製品リソース:
あなたは学生ですか?
ご所属の学校にはすでに Campus-Wide License が導入されていて、MATLAB、Simulink、その他のアドオン製品を利用できる可能性があります。