Statistics and Machine Learning Toolbox には、データを記述、解析、およびモデル化する関数やアプリが用意されています。探索的データ解析のために記述統計、可視化、およびクラスタリングを使用したり、確立分布をデータにあてはめたり、モンテカルロ シミュレーションのために乱数を生成できるほか、仮説検定を行うことも可能です。回帰および分類アルゴリズムにより、分類学習器アプリと回帰学習器アプリを使用して対話的に、または自動化された機械学習 (AutoML) を使用したプログラムで、データから推定を行い予測モデルを作成できます。
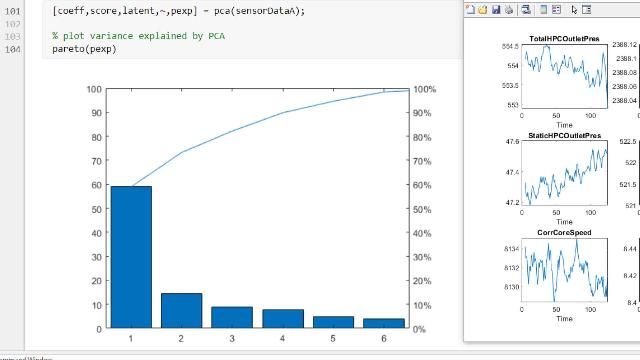
また、多次元データの解析および特徴抽出については、ツールボックスで、主成分分析 (PCA)、正則化、次元削減、特徴選択の手法が提供されており、予測精度を最大限に高める変数の特定が可能です。
このツールボックスには、サポート ベクター マシン (SVM)、ブースティングされた決定木、浅いニューラル ネットワーク、k-means、およびその他のクラスタリング手法を含む、教師あり機械学習、半教師あり機械学習、および教師なし機械学習のアルゴリズムが用意されています。部分従属プロットやシャープレイ値、LIME、および組み込み配布向けの C/C++ コード自動生成などの解釈可能性の手法を適用することができます。ネイティブの Simulink ブロックにより、シミュレーションおよびモデルベースデザイン (MBD、モデルベース開発) で予測モデルを使用することができます。メモリに収まりきらない大きなデータセットに、多くのツールボックス アルゴリズムを使用することができます。
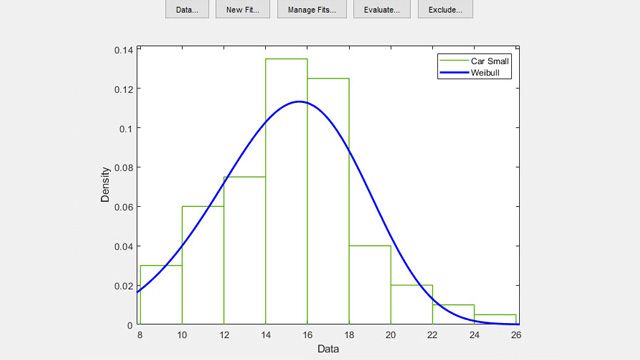
記述統計と可視化
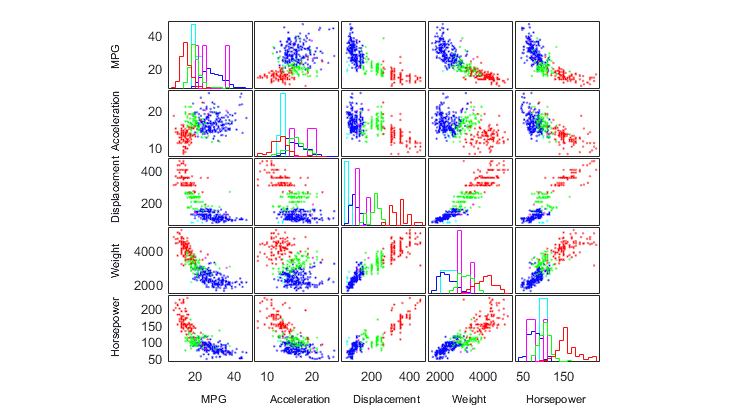
対話型および視覚的グラフィックスによる統計プロット、記述統計を通じてデータを検討します。中心傾向、分散、形状、相関、共分散の測定などの記述統計を使用して、データセットが大規模な場合でもすばやく理解して、記述することができます。
ドキュメンテーション | 例
クラスター分析
k-means、階層、DBSCAN などのクラスタリング手法を適用してパターンや特徴量を特定し、データをグループやクラスターに分割します。さまざまな評価基準を使用して、データに最適なクラスター数を判断します。異常値を検出して、外れ値や新奇性を特定します。
ドキュメンテーション | 例
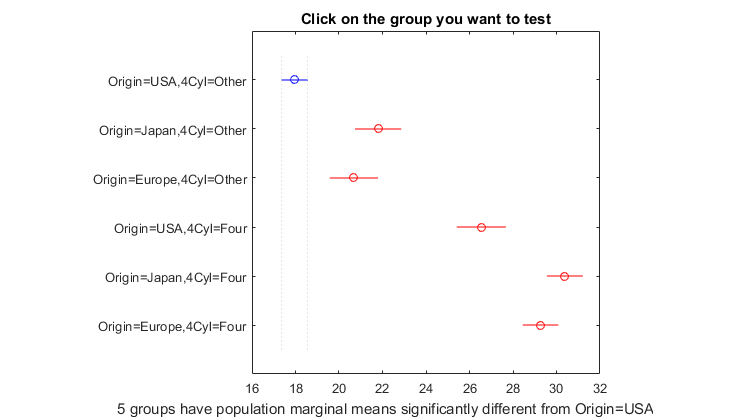
ANOVA
標本分散をいくつかの異なる発生源に割り当て、変動がグループ内で発生したものか、異なるグループ間で発生したものかを決定します。1 因子、2 因子、多因子、多変数、ノンパラメトリック ANOVA、共分散分析 (ANOCOVA)、および反復測定分散分析 (RANOVA) を用います。
ドキュメンテーション | 例
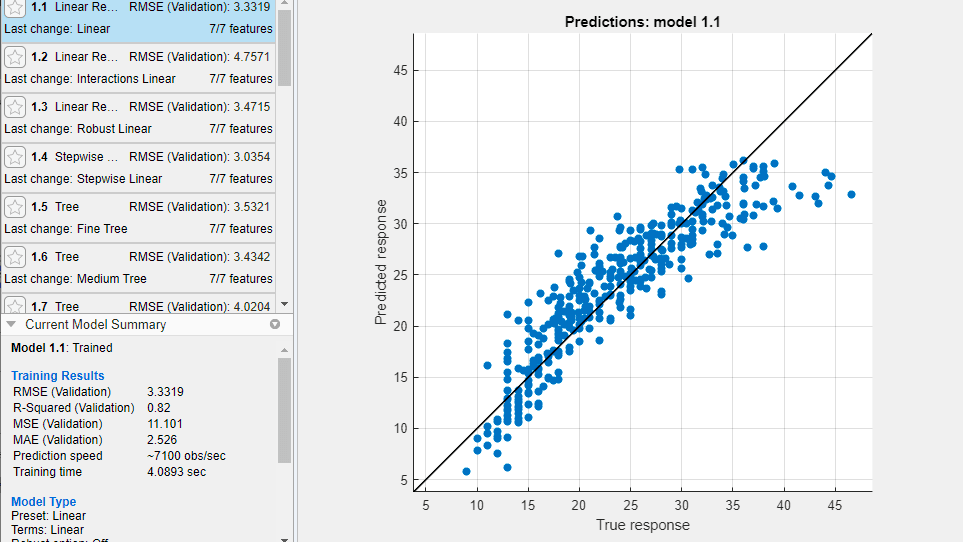
回帰
回帰学習器アプリを使用するか、またはプログラムにより線形回帰、ガウス過程、サポート ベクター マシン、ニューラル ネットワーク、アンサンブルなどのモデルの学習を行い、評価します。
ドキュメンテーション | 例
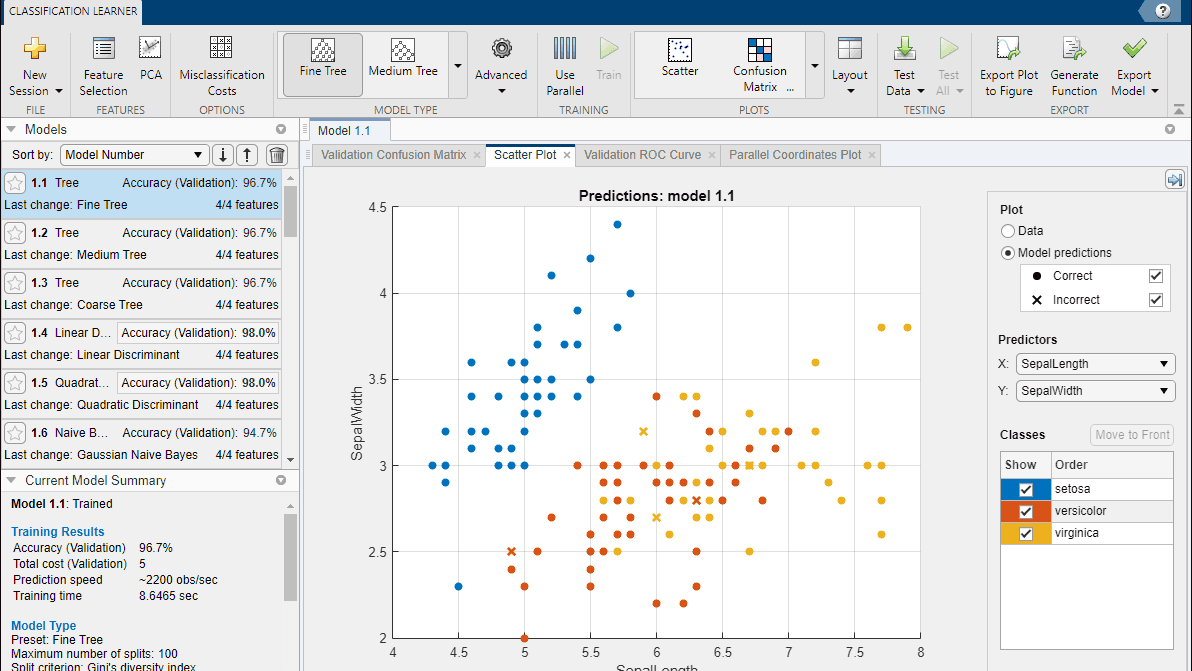
分類
分類学習器アプリを使用するか、またはプログラムによりロジスティック回帰、サポート ベクター マシン、ブースティング木、浅いニューラル ネットワークなどのモデルの学習を行い、検証します。
ドキュメンテーション | 例
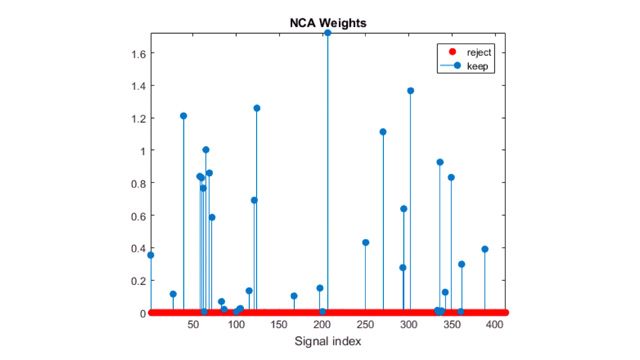
次元削減および特徴抽出
画像、信号、テキスト、および数値データから特徴量を抽出します。繰り返し、新たな特徴量を探索して作成し、性能を最適化する特徴量の組を選択します。既存の特徴量を新しい予測子変数に変換し、変換後に説明的でない特徴量を落とすか、または自動化された特徴選択を適用することによって次元削減を行います。
ドキュメンテーション | 例
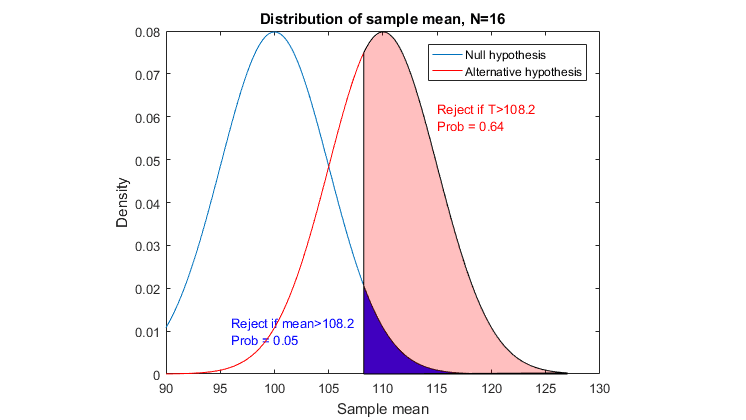
仮説検定
サンプルからの統計的証拠に基づいて、母集団に関する推論を行います。t 検定、分布検定、および 1 標本、対応のある標本、独立した標本のノンパラメトリック検定を行います。自己相関と乱数度の検定を行い、分布を比較します。
ドキュメンテーション | 例
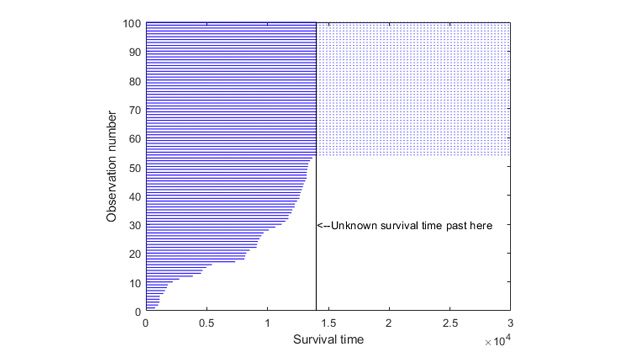
産業統計
効果とデータの傾向を統計的に解析します。データ出力に及ぼす影響の情報を生成するためのデータ入力の操作方法について、実験を設計して実用的な計画を作成、テストします。打ち切りの有無にかかわらず、故障までの時間のデータを可視化して解析し、産業プロセスの品質を監視して評価します。
ドキュメンテーション | 例
tall 配列を使用したビッグデータの分析
分類、回帰、クラスタリングの多くのアルゴリズムで tall 配列および table を使用し、コードを変更することなくメモリに収まりきらないデータセットを使ってモデルを学習させることができます。
ドキュメンテーション | 例
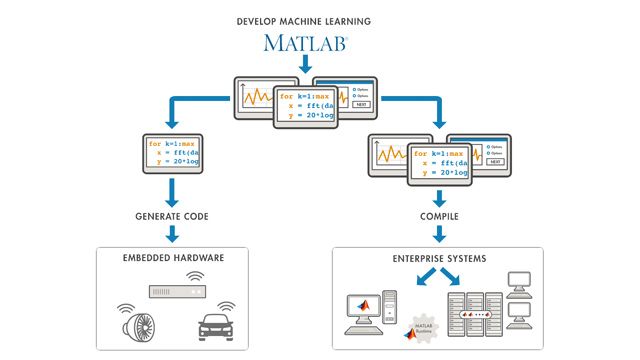
コード生成
分類モデルと回帰モデル、記述統計、および確率分布の推論を行うために、移植可能で可読性に優れた C/C++ コードを生成します。精度を下げて C/C++ 予測コードを生成し、予測コードを再生成せずに、展開済みモデルのパラメーターを更新します。
ドキュメンテーション | 例
製品リソース:
あなたは学生ですか?
ご所属の学校にはすでに Campus-Wide License が導入されていて、MATLAB、Simulink、その他のアドオン製品を利用できる可能性があります。
![[クラスター データ] ライブ エディター タスク MATLAB を使用したクラスター分析。](https://jp.mathworks.com/products/statistics/_jcr_content/mainParsys/band_1749659463_copy/mainParsys/columns/ae985c2f-8db9-4574-92ba-f011bccc2b9f/image_copy.adapt.full.medium.gif/1709642170525.gif)