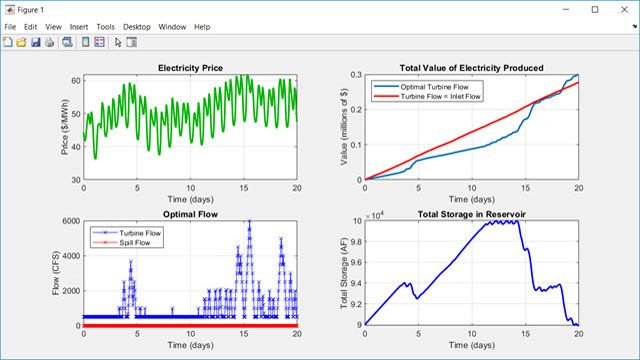
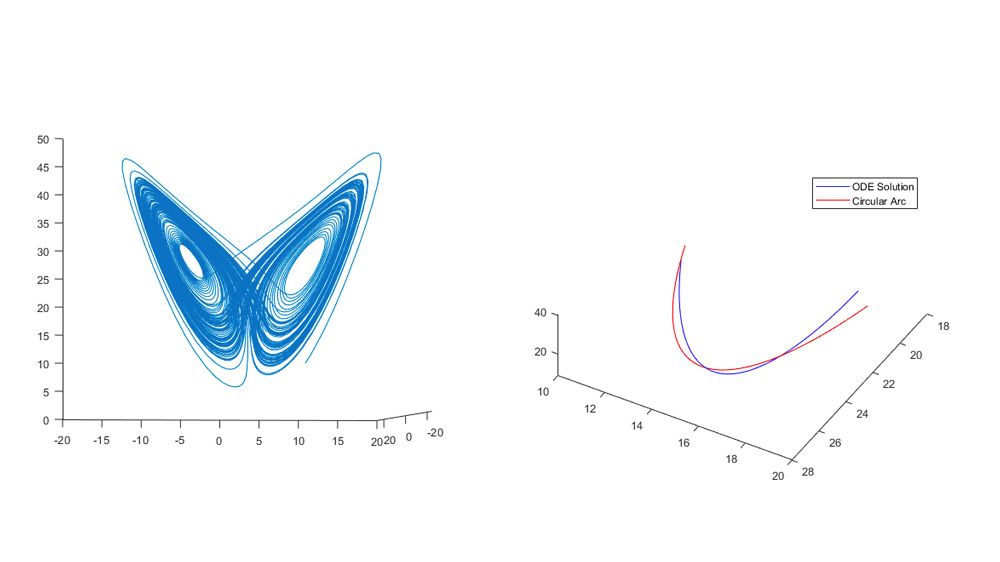
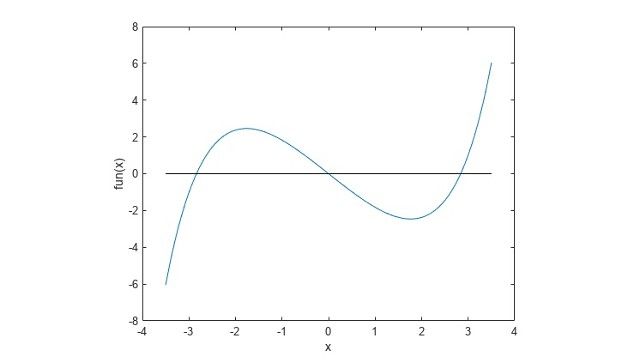
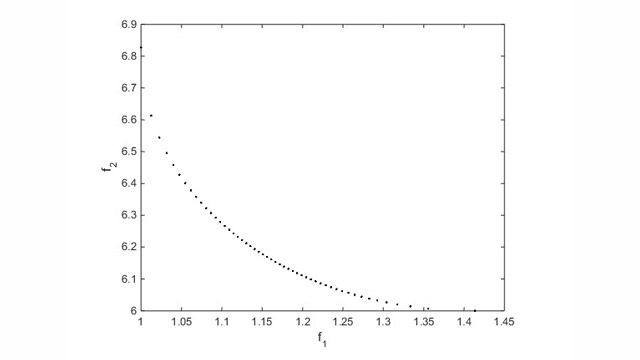
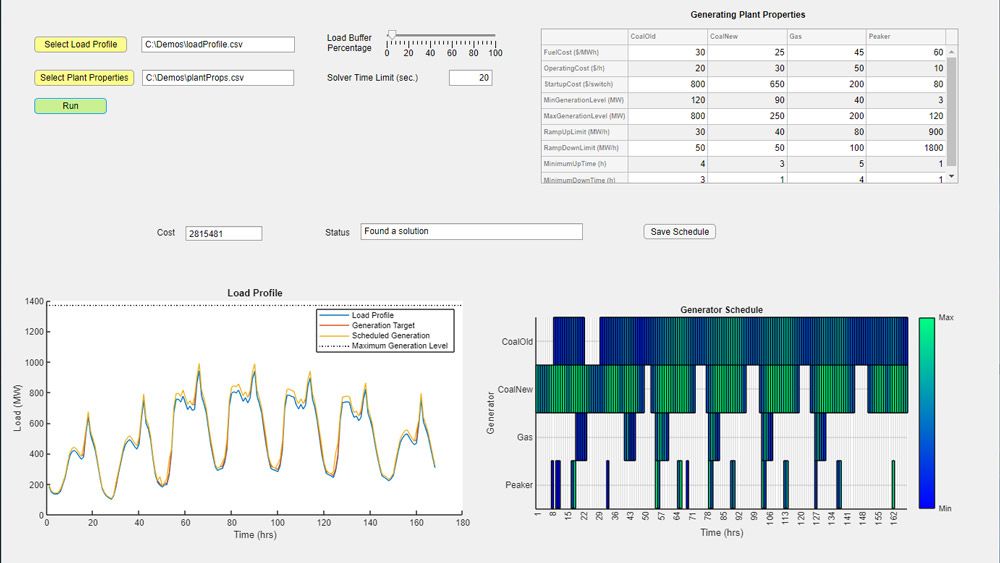
Optimization Toolbox には、制約を満たしながら目的関数を最小化または最大化するパラメーターを見つけるための関数が用意されています。このツールボックスには、線形計画法 (LP) や混合整数線形計画法 (MILP)、二次計画法 (QP)、二次錐計画法 (SOCP)、非線形計画法 (NLP)、制約付き線形最小二乗法、非線形最小二乗法、非線形方程式のソルバーが含まれます。
最適化問題を定義するには、関数や行列を使用するか、基礎となる数学が反映された変数式を指定します。目的関数や制約関数の自動微分を使用することで、迅速かつ正確に求解できます。
ツールボックスのソルバーを使用して連続問題や離散問題の最適解を見つけたり、トレードオフ解析を行ったりするほか、最適化手法をアルゴリズムやアプリケーションに組み込むことができます。このツールボックスを使用して、パラメーターの推定やコンポーネントの選択、パラメーターの調整といった、設計の最適化タスクを行うこともできます。これにより、ポートフォリオの最適化、エネルギー管理および取引、生産計画などの用途の最適解を見つけることができます。
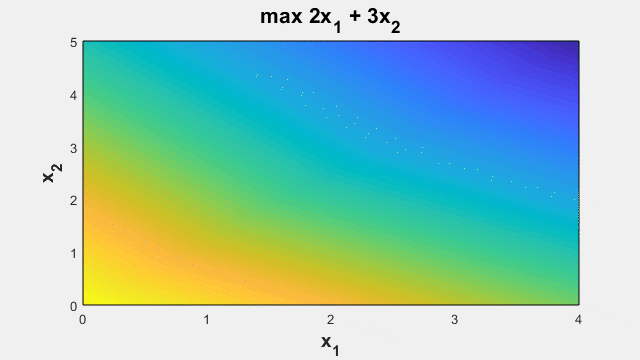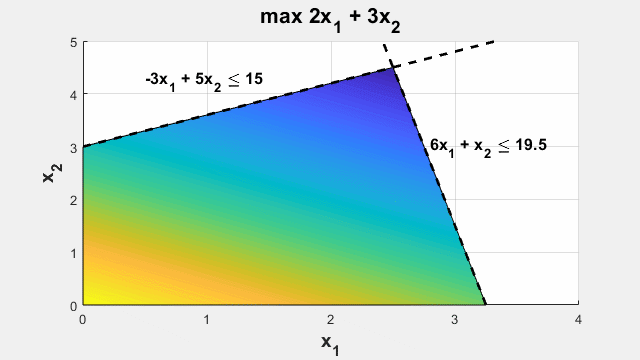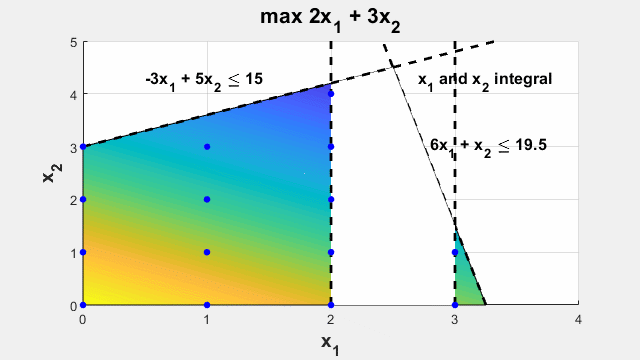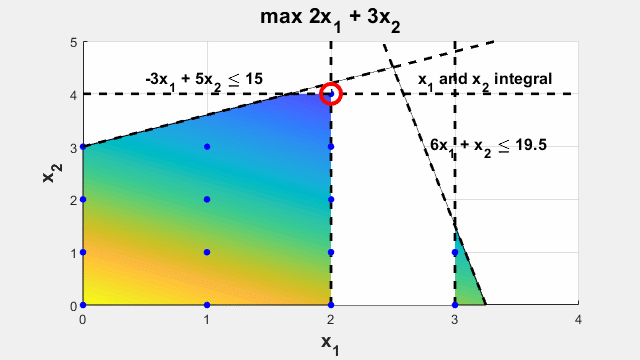
最適化問題の定義
設計問題や決定問題を最適化問題としてモデル化します。設計パラメーターと決定を最適化変数として設定します。変数を使用して最適化する目的関数を定義し、制約を使用して変数値を制限します。
ドキュメンテーション | 例
製品リソース:
「MATLAB は、堅牢な数値アルゴリズム、広範な可視化ツールと解析ツール、信頼性の高い最適化ルーチン、オブジェクト指向プログラミングのサポート、当社の運用 Java アプリケーションと共にクラウドで動作する機能を備えており、当社の研究開発や展開の促進に役立っています。」
Borislav Savkovic, BuildingIQ
あなたは学生ですか?
ご所属の学校にはすでに Campus-Wide License が導入されていて、MATLAB、Simulink、その他のアドオン製品を利用できる可能性があります。