Wavelet Time Scattering Classification of Phonocardiogram Data
This example shows how to classify human phonocardiogram (PCG) recordings using wavelet time scattering and a support vector machine (SVM) classifier. Phonocardiograms are acoustic recordings of sounds produced by the systolic and diastolic phases of the heart. Auscultation of the heart continues to play an important diagnostic role in assessing cardiac health. Unfortunately, many areas of the world lack sufficient numbers of medical personnel trained in heart auscultation. Accordingly, it is necessary to develop reliable automated ways of interpreting phonocardiogram data.
This example uses wavelet scattering as a feature extractor for PCG classification. In wavelet scattering, data is propagated through a series of wavelet transforms, nonlinearities, and averaging to produce low-variance representations of the data. These low-variance representations are then used as inputs to a classifier. This example is a binary classification problem where each PCG recording is either "normal" or "abnormal".
A note on terminology: In the context of wavelet scattering, the term "time windows" refers to the number of samples obtained after downsampling the output of the smoothing operation. For more information, see Time Windows.
Data Description
This example uses phonocardiogram (PCG) data obtained from persons with normal and abnormal cardiac function. The dataset consists of 3829 recordings, 2575 from persons with normal cardiac function and 1254 records from persons with abnormal cardiac function. Each recording is 10,000 samples long and is sampled at 2 kHz. This represents five seconds of phonocardiogram data. The dataset is constructed from the training and validation data used in the PhysioNet Computing in Cardiology Challenge 2016 [1][2].
Download Data
The first step is to download the data from the GitHub repository. To download the data, click Code and select Download ZIP. Save the file physionet_phonocardiogram-main.zip in a folder where you have write permission. The instructions for this example assume you have downloaded the file to your temporary directory, (tempdir in MATLAB®). Modify the subsequent instructions for unzipping and loading the data if you choose to download the data in folder different from tempdir.
The file physionet_phonocardiogram-main.zip contains
PCG_Data.zip
README.md
and PCG_Data.zip contains
heartSoundData.mat
extrafiles.mat
Modified_physionet_data.txt
License.txt.
heartSoundData.mat holds the data and class labels used in this example. The .txt file, Modified_physionet_data.txt, is required by PhysioNet's copying policy and provides the source attributions for the data as well as a description of how each signal in heartSoundData.mat corresponds to a file in the original PhysioNet data. extrafiles.mat also contains source file attributions and is explained in the Modified_physionet_data.txt file. The only file required to run the example is heartSoundData.mat.
Load Data
If you followed the download instructions in the previous section, enter the following commands to unzip the two archive files.
unzip(fullfile(tempdir,"physionet_phonocardiogram-main.zip"),tempdir) unzip(fullfile(tempdir,"physionet_phonocardiogram-main","PCG_Data.zip"), ... fullfile(tempdir,"PCG_Data"))
After you unzip the PCG_Data.zip file, load the data into MATLAB.
load(fullfile(tempdir,"PCG_Data","heartSoundData.mat"))
heartSoundData is a structure array with two fields: Data and Classes. Data is a 10000-by-3829 matrix where each column is an PCG recording. Classes is a 3829-by-1 categorical array of diagnostic labels, one for each column of Data. Because this is a binary classification problem, the classes are "normal" and "abnormal". As previously stated, there are 2575 normal records and 1254 abnormal records. Equivalently, 67.25% of the examples in the data are from persons with normal cardiac function while 32.75% are from persons with abnormal cardiac function. You can verify this by entering:
summary(heartSoundData.Classes)
normal 2575
abnormal 1254
countcats(heartSoundData.Classes)./sum(countcats(heartSoundData.Classes))
ans = 2×1
0.6725
0.3275
Wavelet Scattering Network
Use waveletScattering to construct a wavelet time scattering network. Set the invariant scale to match the signal length. The default scattering network has two wavelet transforms (filter banks). The first wavelet filter bank has eight wavelets per octave. The second filter bank has one wavelet per octave. Set the 'OptimizePath' property to true.
N = 1e4;
sn = waveletScattering(SignalLength=N,InvarianceScale=N, ...
OptimizePath=true);Create Training and Test Sets
The helper function, partition_heartsounds, partitions the 3829 observations so that 70% (2680) are in the training set with 1802 normal and 878 abnormal. The remaining 1149 records (773 normal and 376 abnormal) are held out in the test set for prediction. The random number generator is seeded inside of the helper function so the results are repeatable. The code for partition_heartsounds and all other helper functions used in this example is given in the Supporting Functions section at the end of the example.
[trainData, testData, trainLabels, testLabels] = ...
partition_heartsounds(70,heartSoundData.Data,heartSoundData.Classes);You can check the numbers of each class in the training and test sets.
summary(trainLabels)
normal 1802
abnormal 878
summary(testLabels)
normal 773
abnormal 376
Note that the training and test sets have been partitioned so that the proportion of "normal" and "abnormal" records in the training and test sets are the same as their proportions in the overall data. You can confirm this with the following.
countcats(trainLabels)./sum(countcats(trainLabels))
ans = 2×1
0.6724
0.3276
countcats(testLabels)./sum(countcats(testLabels))
ans = 2×1
0.6728
0.3272
Scattering Features
Obtain the scattering transform of all 2680 recordings in the training set. For multivariate time series, the scattering transform assumes each column is a separate signal. Use the "log" option to obtain the natural logarithm of the scattering coefficients.
scat_features_train = featureMatrix(sn,trainData,Transform="log");For the given scattering parameters, scat_features_train is a 279-by-5-by-2680 matrix. There are 279 scattering paths and five scattering windows for each of the 2680 signals. In order to pass this to the SVM classifier, reshape the tensor into a 13400-by-279 matrix where each row represents a single scattering window across the 279 scattering paths. The total number of rows is equal to the product of 5 and 2680 (number of recordings in the training data).
Nseq = size(scat_features_train,2);
scat_features_train = permute(scat_features_train,[2 3 1]);
scat_features_train = reshape(scat_features_train, ...
size(scat_features_train,1)*size(scat_features_train,2),[]);Repeat the process for the test data.
scat_features_test = featureMatrix(sn,testData,Transform="log"); scat_features_test = permute(scat_features_test,[2 3 1]); scat_features_test = reshape(scat_features_test, ... size(scat_features_test,1)*size(scat_features_test,2),[]);
Here we replicate the labels so that we have a label for each scattering time window.
[sequence_labels_train,sequence_labels_test] = ...
createSequenceLabels_heartsounds(Nseq,trainLabels,testLabels);Fit the SVM to the training data. In this example, we use a cubic polynomial kernel. After fitting the SVM to the training data, we perform a 5-fold cross-validation to estimate the generalization error on the training data. Here each scattering window is classified separately.
rng default; classificationSVM = fitcsvm( ... scat_features_train, ... sequence_labels_train , ... KernelFunction="polynomial", ... PolynomialOrder=3, ... KernelScale="auto", ... BoxConstraint=1, ... Standardize=true, ... ClassNames=categorical({'normal','abnormal'})); kfoldmodel = crossval(classificationSVM, KFold=5);
Compute the loss as a percentage and display the confusion matrix.
predLabels = kfoldPredict(kfoldmodel);
loss = kfoldLoss(kfoldmodel)*100;
fprintf("Loss is %2.2f percent\n",loss);Loss is 0.96 percent
accuracy = 100-loss;
fprintf("Accuracy is %2.2f percent\n",accuracy);Accuracy is 99.04 percent
confmatCV = confusionchart(sequence_labels_train,predLabels);

Note that the scattering network results in approximately 99 percent accuracy when each time window is classified separately. However, the performance is actually better than this value because we have five scattering windows per recording and the 99 percent accuracy is based on classifying all windows separately. In this case, use a majority vote to obtain a single class assignment per recording. The class vote corresponds to the mode of the votes for the five windows. If no unique mode is found, the helper function helperMajorityVote classifies that set of scattering windows as 'NoUniqueMode' to indicate a classification error. This results in an extra column in the confusion matrix.
classes = categorical({'abnormal','normal'});
ClassVotes = helperMajorityVote(predLabels,trainLabels,classes);
CVaccuracy = sum(eq(ClassVotes,trainLabels))./numel(trainLabels)*100;
fprintf("The true cross-validation accuracy is %2.2f percent.\n",CVaccuracy);The true cross-validation accuracy is 99.89 percent.
Display the confusion matrix for the majority vote classifications.
cmCV = confusionchart(trainLabels,ClassVotes);
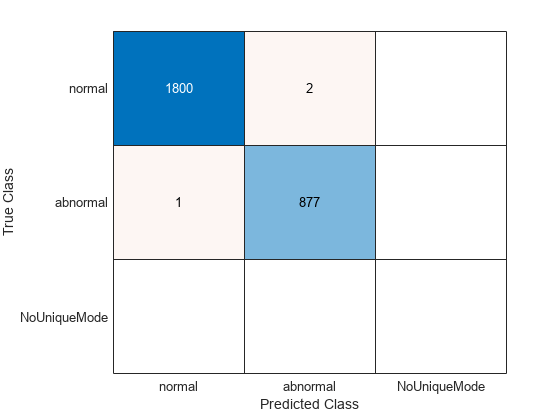
The cross-validation accuracy on the training data is actually 99.89 percent. There are two normal records, which are misclassified as abnormal. One abnormal record is classified as normal.
Use the SVM model fit to the training data to make class predictions on the held-out test data.
predTestLabels = predict(classificationSVM,scat_features_test);
Determine the accuracy of the predictions on the test set using a majority vote.
ClassVotes = helperMajorityVote(predTestLabels,testLabels,classes);
testaccuracy = sum(eq(ClassVotes,testLabels))./numel(testLabels)*100;
fprintf("The test accuracy is %2.2f percent.\n",testaccuracy);The test accuracy is 91.82 percent.
cmTest = confusionchart(testLabels,ClassVotes);
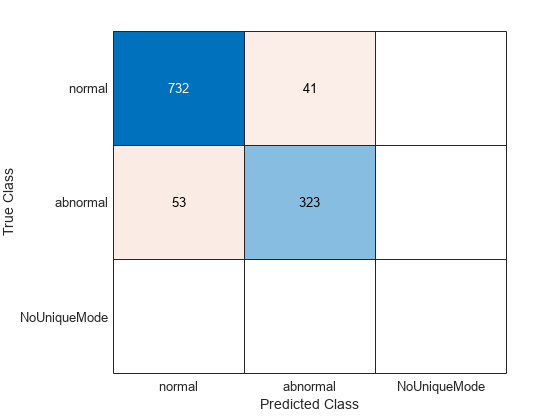
Of the 1149 test records, approximately 92% are correctly classified as "Normal" or "Abnormal". Of the 773 normal PCG recordings in the test set, 732 are correctly classified. Of the 376 abnormal recordings in the test set, 323 are correctly classified.
Precision, Recall, and F1 Score
In a classification task, the precision for a class is the number of correct positive results divided by the number of positive results. In other words, of all the records that the classifier assigns a given label, what proportion actually belong to the class. Recall is defined as the number of correct labels divided by the number of labels for a given class. Specifically, of all the records belonging to a class, what proportion did our classifier label as that class. In judging the accuracy your classifier, you ideally want to do well on both precision and recall. For example, suppose we had a classifier that labeled every PCG recording as abnormal. Then our recall for the abnormal class would be 100%. All records belonging to the abnormal class would be labeled abnormal. However, the precision would be low. Because our classifier labeled all records as abnormal, there would be 2575 false positives in this case for a precision of 1254/3829, or 32.75%. The F1 score is the harmonic mean of precision and recall and provides a single metric that summarizes the classifier performance in terms of both recall and precision. The helper function, helperF1heartSounds, computes the precision, recall, and F1 scores for the classification results on the test set and returns those results in a table.
PRTable = helperF1heartSounds(cmTest.NormalizedValues); disp(PRTable)
Precision Recall F1_Score
_________ ______ ________
Abnormal 88.736 85.904 87.297
Normal 93.248 94.696 93.967
In this case, the F1 scores for the abnormal and normal groups confirm that our model has both good precision and recall. In binary classification it is simple to determine both precision and recall directly from the confusion matrix. To see this, plot the confusion matrix again for convenience.
cmTest = confusionchart(testLabels,ClassVotes);
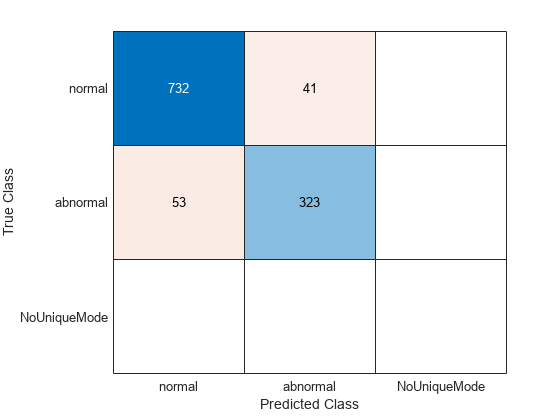
The recall for the abnormal class is the number of abnormal records identified as abnormal, which is the entry in the second row and second column of the confusion matrix divided by the sum of entries in the second row. Precision for the abnormal class is the proportion of true abnormal records in the total number identified as abnormal by the classifier. That corresponds to the entry in the second row and second column of the confusion matrix divided by the sum of entries in the second column. The F1 score is the harmonic mean of the two.
RecallAbnormal = cmTest.NormalizedValues(2,2)/sum(cmTest.NormalizedValues(2,:)); PrecisionAbnormal = cmTest.NormalizedValues(2,2)/sum(cmTest.NormalizedValues(:,2)); F1Abnormal = harmmean([RecallAbnormal PrecisionAbnormal]); fprintf("RecallAbnormal = %2.3f\nPrecisionAbnormal = %2.3f\nF1Abnormal = %2.3f\n", ... 100*RecallAbnormal,100*PrecisionAbnormal,100*F1Abnormal);
RecallAbnormal = 85.904 PrecisionAbnormal = 88.736 F1Abnormal = 87.297
Repeat the above for the normal class.
RecallNormal = cmTest.NormalizedValues(1,1)/sum(cmTest.NormalizedValues(1,:)); PrecisionNormal = cmTest.NormalizedValues(1,1)/sum(cmTest.NormalizedValues(:,1)); F1Normal = harmmean([RecallNormal PrecisionNormal]); fprintf("RecallNormal = %2.3f\nPrecisionNormal = %2.3f\nF1Normal = %2.3f\n", ... 100*RecallNormal,100*PrecisionNormal,100*F1Normal);
RecallNormal = 94.696 PrecisionNormal = 93.248 F1Normal = 93.967
Summary
This example used wavelet time scattering to robustly identify human phonocardiogram recordings as normal or abnormal in a binary classification problem. Wavelet scattering required only the specification of a single parameter, the length of the scale invariant, in order to produce low-variance representations of the PCG data that enabled the support vector machine classifier to accurately model the difference between the two groups. The support vector machine classifier with wavelet scattering was able to achieve superior performance in both precision and recall for both groups in spite of significantly unbalanced numbers of normal and abnormal PCG recordings in both the training and test set.
References
Goldberger, A. L., L. A. N. Amaral, L. Glass, J. M. Hausdorff, P. Ch. Ivanov, R. G. Mark, J. E. Mietus, G. B. Moody, C.-K. Peng, and H. E. Stanley. "PhysioBank, PhysioToolkit, and PhysioNet: Components of a New Research Resource for Complex Physiologic Signals". Circulation. Vol. 101, No. 23, 13 June 2000, pp. e215-e220. http://circ.ahajournals.org/content/101/23/e215.full
Liu et al. "An open access database for the evaluation of heart sound algorithms". Physiological Measurement. Vol. 37, No. 12, 21 November 2016, pp. 2181-2213. https://www.ncbi.nlm.nih.gov/pubmed/27869105
Supporting Functions
partition_heartsounds creates training and test sets consisting of specified proportions of the data. The function also preserves the proportion of abnormal and normal PCG recordings in each set.
function [trainData, testData, trainLabels, testLabels] = partition_heartsounds(percent_train_split,Data,Labels) % This function is only in support of the Wavelet Time Scattering % Classification of Phonocardiogram Data example. It may change or be % removed in a future release. % Labels in heart sound data are not sequential. percent_train_split = percent_train_split/100; % Each column is an observation NormalData = Data(:,Labels == 'normal'); AbnormalData = Data(:,Labels == 'abnormal'); LabelsNormal = Labels(Labels == 'normal'); LabelsAbnormal = Labels(Labels == 'abnormal'); Nnormal = size(NormalData,2); Nabnormal = size(AbnormalData,2); num_train_normal = round(percent_train_split*Nnormal); num_train_abnormal = round(percent_train_split*Nabnormal); rng default; Pnormal = randperm(Nnormal,num_train_normal); Pabnormal = randperm(Nabnormal,num_train_abnormal); notPnormal = setdiff(1:Nnormal,Pnormal); notPabnormal = setdiff(1:Nabnormal,Pabnormal); trainNormalData = NormalData(:,Pnormal); trainNormalLabels = LabelsNormal(Pnormal); trainAbnormalData = AbnormalData(:,Pabnormal); trainAbnormalLabels = LabelsAbnormal(Pabnormal); testNormalData = NormalData(:,notPnormal); testNormalLabels = LabelsNormal(notPnormal); testAbnormalData = AbnormalData(:,notPabnormal); testAbnormalLabels = LabelsAbnormal(notPabnormal); trainData = [trainNormalData trainAbnormalData]; trainData = (trainData-mean(trainData))./std(trainData,1); trainLabels = [trainNormalLabels; trainAbnormalLabels]; testData = [testNormalData testAbnormalData]; testData = (testData-mean(testData))./std(testData,1); testLabels = [testNormalLabels; testAbnormalLabels]; end
createSequenceLabels_heartsounds creates class labels for the wavelet time scattering sequences.
function [sequence_labels_train,sequence_labels_test] = createSequenceLabels_heartsounds(Nseq,trainLabels,testLabels) % This function is only in support of the Wavelet Time Scattering % Classification of Phonocardiogram Data example. It may change or be % removed in a future release. Ntrain = numel(trainLabels); trainLabels = repmat(trainLabels',Nseq,1); sequence_labels_train = reshape(trainLabels,Nseq*Ntrain,1); Ntest = numel(testLabels); testLabels = repmat(testLabels',Nseq,1); sequence_labels_test = reshape(testLabels,Ntest*Nseq,1); end
helperMajorityVote implements a majority vote for a classification based on the mode. If no unique mode is present, a vote of NoUniqueMode is returned to ensure a classification error is recorded.
function [ClassVotes,ClassCounts] = helperMajorityVote(predLabels,origLabels,classes) % This function is in support of Wavelet Toolbox examples. It may % change or be removed in a future release. % Make categorical arrays if the labels are not already categorical predLabels = categorical(predLabels); origLabels = categorical(origLabels); % Expects both predLabels and origLabels to be categorical vectors Npred = numel(predLabels); Norig = numel(origLabels); Nwin = Npred/Norig; predLabels = reshape(predLabels,Nwin,Norig); assert(size(predLabels,2) == length(origLabels)); ClassCounts = countcats(predLabels); [~,idx] = max(ClassCounts); ClassVotes = classes(idx); % Check for any ties in the maximum values and ensure they are marked as % error if the mode occurs more than once modecnt = modecount(predLabels,string(classes)); ClassVotes(modecnt>1) = categorical({'NoUniqueMode'}); ClassVotes = ClassVotes(:); %------------------------------------------------------------------------- function modecnt = modecount(predlabels,classes) % Ensure there is a unique mode modecnt = zeros(size(predlabels,2),1); for nc = 1:size(predlabels,2) hc = histcounts(predlabels(:,nc),classes); hc = hc-max(hc); if sum(hc == 0) > 1 modecnt(nc) = 1; end end end end
helperF1heartSounds calculate precision, recall, and F1 scores for the classifier results.
function PRTable = helperF1heartSounds(confmat) % This function is only in support of the Wavelet Time Scattering % Classification of Phonocardiogram Data example. It may change or be % removed in a future release. precisionAB = confmat(2,2)/sum(confmat(:,2))*100; precisionNR = confmat(1,1)/sum(confmat(:,1))*100 ; recallAB = confmat(2,2)/sum(confmat(2,:))*100; recallNR = confmat(1,1)/sum(confmat(1,:))*100; F1AB = 2*(precisionAB*recallAB)/(precisionAB+recallAB); F1NR = 2*(precisionNR*recallNR)/(precisionNR+recallNR); % Construct a MATLAB Table to display the results. PRTable = array2table([precisionAB recallAB F1AB;... precisionNR recallNR F1NR],... 'VariableNames',{'Precision','Recall','F1_Score'},'RowNames',... {'Abnormal','Normal'}); end
See Also
Related Examples
- Acoustic Scene Recognition Using Late Fusion
- Fault Detection Using Wavelet Scattering and Recurrent Deep Networks
